![]()
接下来,我们介绍 Schema、Identity 和 Context。在上一章,我们将以节点和边组成的数据集合称之为“Data graph”,而真正意义上的知识图谱(knowledge graph)是经过了 Schema(数据模式)、Identity(数据一致性)、Context(上下文)、ontology(本体)和 rules(规则)等表示方法增强过的 data graph。本章我们讨论 Schema、Identity 和 Context。Ontology 和 rules 在后面章节讨论。
3. Schema, Identity, Context
3.1 Schema
相比于关系型数据库的数据模型,图数据的一大优势就是不需要数据模式(schema)或者可以延后定义数据模式。但是给图数据制定数据模式可以规范一些更加高级的结构或者语义。接下来我们讨论三种图数据模式:semantic,validating,emergent。
3.1.1 Semantic schema
语义模式的允许定义图中的高级项的意义,我们可以用这些项进行推理。
根据示例图谱,我们可以定义一些类别(class),比如 Event,City 等等,然后根据类别定义一些子类(subclass),从而形成一个层级结构:

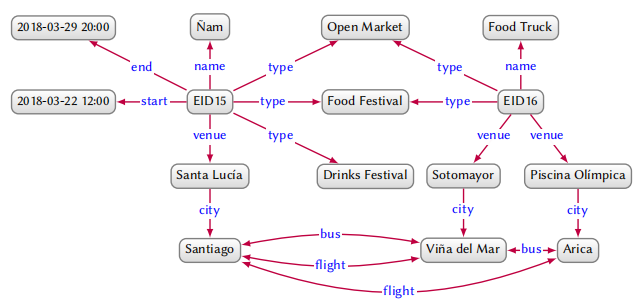
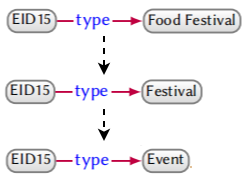
有了这样一个层级结构,我们可以直接从数据中检索到(EID15,type,Food Festival),然后根据语义模式推理出(EID15,type,Festival),进一步推理出(EID15,type,Event),如下所示:
除了类别,我们还希望定义边上标签的语义,即属性(property)。回到示例图谱,我们可以认为 city 和 venue 是 location 的子属性(sub-property),或者 bus 和 flight 是 connections to 的子属性。这样,属性也可以形成一个层级结构。
更进一步,我们可以给属性定义定义域(domain)和值域(range)。定义域表示节点的类别,而边是从该节点扩展出来的。比如,定义 connections to 的定义域为 city,那么对于(Arica connections to Santiago)来说,我们可以推理出(Arica,type,city)。而值域同样表示节点的类别,而边是扩展到该节点上。比如,定义 connections to 的值域是 city,那么那么对于(Arica, connections, to Santiago)来说,我们可以推理出(Santiago,type,city)。
RDF Schema(RDFS)是定义语义模式的一个重要标准,在 RDFS 中我们可以定义类(class)、子类(subclass)、属性(property)、子属性(sub-property)、定义域(domain)和值域(range),并且可以将这些定义进行序列化。

下面给出一个例子:

由于 RDFS 的表达能力较弱,比如无法表示两个实体是同一实体(乔丹,same as,飞人),后来又衍生出另一个非常重要的语义模式——OWL(Web Ontology Language)。OWL 的语义表达能力更强,同时也支持 RDFS,在实际的工程中 OWL 的应用更加广泛。
无论是 RDFS 还是 OWL,包括 OWL 2 等所有的语义模式标准,本质上都是词表。这些词表被认为是语义模式的标准词表,我们用这个词表中的词进行语义建模实现了语义标准化,避免了利用自然语言进行语义建模的歧义性和多样性为后续的推理带来困扰,同时也为多图谱融合提供了方便。我们在后续的文章中进行详细讲解。
语义模式同时也满足一个知识图谱的重要假设——开放世界假设:
当前没有陈述的事情是未知的。
即,没有在知识图谱中描述的知识,我们认为是未知的,而不是不存在的。比如在我们的示例图谱中找不到(Viña del Mar,flight ,Arica)这样一条关系,这不代表在 Viña del Mar 和 Arica 之间是没有航班的,只能说明我们现在还不知道这两地之间有没有航班。
开放世界假设从逻辑上讲是很合理的,因为我们不可能在知识图谱中描述所有的知识,我们只需要描述我们所需要的知识就可以了。但是这样也会给我们带来一定的麻烦,在开放世界假设下,知识图谱无法回答“是”或“否”的问题。比如“在 Viña del Mar 和 Arica 之间有航班吗?”这样一个问题,知识图谱无法直接回答“有”或者“没有”。
相对于开放世界假设,还存在一个封闭世界假设:
没有描述的事情就是不存在的。
即,假设我们的图谱已经是完备的了,它包含了一切知识。
处于开放世界假设和封闭世界假设之间,还有一个局部封闭世界假设:
假设部分没有描述的事情真的不存在。
即,认为我们的图谱是部分完备的。比如假设我们的图谱中已经包含了所有航空公司的所有航线,在所有这些航线中都没有 Viña del Mar 和 Arica 之间的航班,那么我们就认为这两地之间确实没有航班。
3.1.2 Validating schema
如果图谱中的数据多样性较高且存在大量不完备的信息,那么开放世界假设作为默认语义是比较合理的。但是在某些场景下,我们必须保证数据的完备性。比如我们必须保证示例图谱中每一项活动都至少有一个名字、举办地点、开始时间和结束时间,这样才能保证用户对这项活动有最基础的了解。为了保证这些数据的完备性,我们必须对图谱添加一些约束,而 validating schema 就是去验证图谱是否满足我们添加的约束的。
- Semantic schema 用于从现有的知识中推理出新的知识
- Validating schema 用于验证已有的知识的合法性
定义 validating schema 的标准方法是使用 shapes。
其中的 $nodes$ 选取可以是一个类别的所有实例,或者某个属性的定义域或者值域,或者某条查询语句的结果等等。$constraints$ 就是作用在这些节点上的约束条件,比如给定属性上节点的数量,节点的数据类型等等。多个 shape 相互关联就形成了 shapes graph。
Shapes graph 可以用类似 UML 示意图来表示,如下图所示:
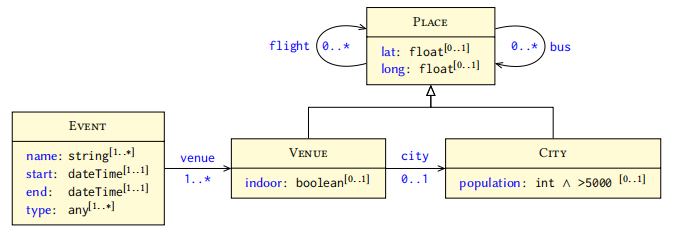
这个例子中包含 4 个 shape:Event、Venue、City 以及 Place,每个 shape 中都对该类别下的节点做出了限制,比如 Event 要求必须包含 name(数据类型是字符串类型)、start(数据类型是日期类型)、end(数据类型是日期类型) 和 type(任意类型)等。其中的 $[1..*]$ 表示可以有 $1-\infty$ 个值,$[1..1]$ 表示只能有 1 个值,$[0..1]$ 表示要么没有值(即可以缺省),要么只能有一个值。
当我们定义了这样一个 shape graph之后,就可以通过递归的方法对数据进行检查,比如 EID15 包含定义的 4 个属性,与之相连的 Santa Lucía 必须属于 Venue 且 Santiago 属于 City。因为 City 属于 Place,就要求 Viña del Mar 和 Arica 也必须属于 Place 等等。而 EID16 就是一个不合法的节点,因为它缺少了 start 和 end。
当我们定义 shape graph 时,不可能知道每个节点包含的所有属性。这种情况下,open shape 允许节点存在在 shape graph 中未定义的属性,而 close shape 则不允许这种情况。比如我们在示例图谱中添加一个关系(Santiago,founder,Pedro de Valdivia),在我们定义的 shape graph 中没有包含 founder 这个属性,在 open shape 情况下,Santiago 仍然是一个合法的节点,但是在 close shape 情况下就变成了非法节点。
实际的查询语言通常还支持额外的特性:AND、OR、NOT 等操作。比如 $\text{Venue}~ AND~ (NOT~ \text{City})$ 表示 venue 不能是 City。但是这些额外的操作符的自由组合可能会造成语义问题,比如著名的理发师悖论:
假设有一个 shape 是(Barber,shave,Person),并且要求 $\text{Person}~ AND~ (NOT~ \text{Barber})$。现在给定(Bob,shave,Bob),其中 Bob 满足 (Bob,,type,Person),那么 Bob 满足(Bob,type,Barber)吗?
如果满足,那么这条数据就是非法的,因为 $\text{Person}~ AND~ (NOT~ \text{Barber})$;
如果不满足,那么这条数据也是非法的,因为它不满足(Bob,type,Barber)。
为了避免这些悖论的产生,人们提出了各种方法,比如分层( stratification)、部分赋值(partial assignments)、稳定模型(stable models)等。
虽然,Semantic schema 和 Validating schema 有不同的应用场景,但是二者也可以互补。我们可以利用 Semantic schema 对 shape 进行推理,也可以利用 Validating schema 对推理结果进行筛选。通常这种情况下需要用 open shape。
目前有两种验证模式语言:Shape Expressions (ShEx) 和 SHACL (Shapes Constraint Language)。更加详细的介绍可以看 Labra Gayo 等人的论文。
3.1.3 Emergent schema
无论是 semantic schema 还是 validating schema 都需要领域专家来构建,但是通常我们不具备这样的条件。我们可以从图谱中抽取一些隐式结构形成 emergent schema。
用于定义 emergent schema 的框架是 quotient graphs,它可以根据一些等价关系划分数据图中的节点组,同时保留图的一些结构属性。比如示例图谱中,我们可以区分不同的 type,比如 event、name、venue、class、date-time、city 等。将每一个 type 的节点融合进一个节点然后保留边,最终形成 quotient graph,如下图所示:
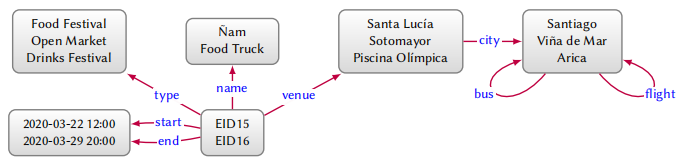
quotient graphs 的定义取决于如何选取节点和边,不同的 quotient graphs 展现出来的图结构不同。严格意义上来说,quotient graphs 是在模拟输入图谱,这就意味着当且仅当 $x \in X, z \in Z$,且 $x \xrightarrow{y} z$ 时,$X \xrightarrow{y} Z$ 才成立。然而示例图谱中 EID16 是没有开始和结束时间的,所以我们应该将上图换成:
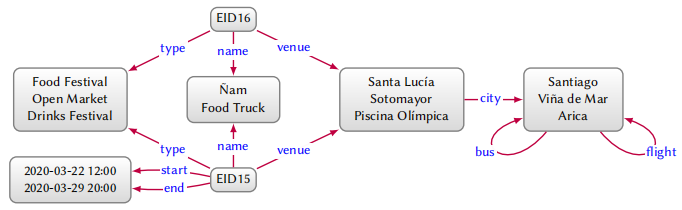
将 event 分成两个节点来保存满足不同边的节点,这样的图叫做 bisimilarity。关于 bisimilarity 的一个比较严格的定义是:当存在 $X \xrightarrow{y} Z$ 关系时,对于任意 $x \in X$,必定存在 $z \in Z$ 满足 $x \xrightarrow{y} z$。
3.2 Identity
在示例图谱中,我们有一个节点 “Santiago”,但是到底是哪个 Santiago?是 Santiago de Chile?Santiago de Cuba?Santiago de Compostela?甚至说是摇滚乐队 Santiago?从(Santa Lucía,city,Santiago)我们可以推出 Santiago 是一个城市而不是乐队,另一方面,这个图谱是关于智利的旅游图谱,那么我们可以推理出这里的 Santiago 应该是 Santiago de Chile。如果没有足够多的信息,节点的歧义性就会给后续的任务带来麻烦。为了避免节点的歧义性,首先要做的就是给节点分配全局统一的标识符,其次就是给节点添加外部链接标识符加以以区分。
3.2.1 Persistent identifiers
假设我们想对比智利和古巴的旅游景点,我们收集了足够多的数据然后分别构建了图谱。当我们想要将两个图谱融合在一起的时候就会出现问题:
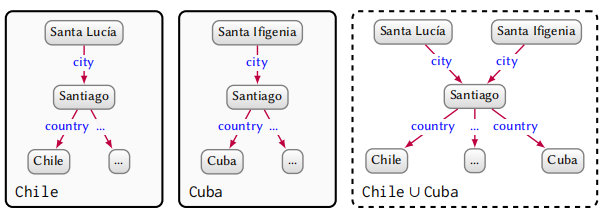
如图所示,两个图谱都有 Santiago 节点,我们如果直接合并的话,两个 Santiago 就会合并成一个。但是我们知道实际上两个 Santiago 是两个不同的地点。为了避免这种情况,我们可以给每个 Santiago 分配一个 Persistent identifiers(PIDs),每一个 PID 保证其全局唯一性。
除了全局唯一性,我们通常还需要在网页对图谱进行展示,所以 RDF 推荐使用 IRI 来表示实体和关系。比如:

IRI 的形式与 URL 非常相近,如果我们把上面的 IRI 复制到浏览器的话,我们会发现进入到了维基百科的页面。那么 IRI 和 URL 有什么区别呢?URL 是用于信息资源的定位,所谓信息简单来说其实就是网页,比如 URL “https://www.wikidata.org/wiki/Q2887” 表示的是关于 “Santiago” 这个网页而不是 “Santiago” 这个实体。为了更进一步解释其中的区别,我们来看下面的例子:

与上面 IRI 表示法一模一样,但是如果这里是 URL 的话,实际上会给我们带来歧义:到底是 Santiago 这个城市是由 Pedro de valdivia 建立的,还是 “Santiago” 这个网页是 Pedro de valdivia 创建的?
3.2.2 External identity links
假设在我们的图谱中定义了 Santiago 节点为 chile:Santiago
chile 是 “http://turismo.cl/entity/” 的缩写,这个节点定义相当于 “http://turismo.cl/entity/Santiago”
在另一个地理相关的图谱中定义了 Santiago 为 geo:SantiagoDeChile。两个节点实际上指得是同一座城市,但是由于命名不同,我们就灭哟哟办法直接知道这两个节点是相同的。如果我们对来弄个图谱进行融合的时候,会造成同一个实体有两个不同的节点。
将两个名称不同,但是表示同一实体的节点统一的方法有以下几种:
使用实体在图谱中信息的唯一性,比如地理坐标、邮政编码、成立时间等;
使用标识链接来声明本体实体与外部源中发现的实体是相同实体。在 OWL 中定义了
owl:sameAs属性来关联两个实体。例如:
3.2.3 Datatypes
思考一下示例图谱中左侧的两个日期:“2020-03-29T20:00:00” 和 “2020-03-22T12:00:00”,我们应该怎样分配 PID?直观上来说,我们给它们分配的 IRI 需要告诉我们特定的日期和时间,并且可以被机器或者软件识别,然后我们还可以对这些值进行排序,抽取我们需要的年份、月份等。
大多数图数据模型允许定义节点的数据类型。RDF 使用 XML Schema Datatypes (XSD),表示为($l, d$)对 ,其中 $l$ 表示词汇字符串,$d$ 表示数据类型。比如
1 | “2020-03-29T20:00:00” 就表示成 "2020-03-29T20:00:00"^^xsd:dateTime |
RDF 中数据类型节点被称为 “literals”,并且不允许有向外的边。RDF 中其他常用的数据类型还包括:xsdstring、xsd:integer、xsd:decimal、xsd:boolean 等等。
建立在图谱之上的应用可以通过识别这些数据类型,对其进行解析然后做排序、变换等等后续的处理。
3.2.4 Lexicalisation
虽然通常 PID 的形式具有人类可解释性,但是 PID 本身不具有任何语义信息,比如 chile:Santiago。甚至有时候 PID 连人类可解释性都不具备,比如 wd:Q2887。这两种表示法分别称为显式表示和隐式表示,显式表示法有利于人类理解,而隐式表示有利于持久化,比如假设我,们用 wd:Q2887 表示某公司某部门的员工,如果该员工工作部门发生了变动,采用显式表示的话其对应的节点就需要改变,而如果采用隐式表示就无序改变。
由于 PID 具有任意性,所以通常会给节点添加一个人类可读的边作为标记,比如:

实际上可以将这种标记看成是编程语言中的注释,用来说明特定节点在真实世界中包含的信息。我们可以使用昵称或者注释来实现:


形如 "Santiago" 这样的节点通常是 literal,而不是标识符。不同的图谱会有不同的表示,比如 (Santiago, rdfs:label, "City"@en) 或者 (Santiago, rdfs:label, "Ciudad"@es) 表示不同语言下的注释。这种用人类可读的 labels,aliases,comments 来对节点进行注释的图谱,我们称之为 “ (multilingual) lexicalised knowledge graphs ”。
3.2.5 Existential nodes
当建模不完整的信息时,我们在某些情况下可能知道图中必须存在一个特定的节点,与其他节点有特定的关系,但无法识别所讨论的节点。比如两个活动 chile:EID42 和 chile:EID43 有共同的活动地点,但是这个活动地点还没有公布。这种情况的一种处理方法就是忽略活动地点这个关系,但是这样我们会丢失一些信息:
- 活动是有活动地点这个属性的;
- 两个活动有相同的举办地点。
另一种处理方法就是创建一个新的 IRI,但是这样的话又无法区分未知地点和已知地点的区别。因此,一些图谱中允许空节点的存在,即所谓的 existential nodes:

在 RDF 中支持空节点的存在,即 blank nodes。Blank nodes 也被用来对复杂元素进行建模,比如 RDF list:

3.3 Context
我们可以认为在某些特定情况下,图谱中的数据都是真实的。但是如果考虑时效性的话,Santiago 是从 1541 年成为一个城市的,而 Arica 到 Santiago 的航班是 1956 年开通的。考虑地理因素的话,示例图谱描述的是 chile。考虑数据来源的话,与 EID15 相关的数据来源于 2020 年 1 月 4 日的 Ñam 网页。因此,通过上面的例子,我们可以看到,图谱中的知识都是具有片面性的,只在某些特定情境下成立,这些特定情形我们称之为 context。现在我们就来介绍不同级别的 context 的不同表示方法。
3.3.1 Direct representation
第一种表示方法就是把 context 当成图谱数据的一部分,用节点和边来表示,比如 EID15 关联的日期时间,我们就认为在这个时间上 (EID15,venueSanta Lucia) 是成立的。另一种方法就如我们在第二章介绍属性图那样,改变边的模式。虽然我们的例子中用的是比较随意的方法,但是实际上有一些特定的 context 已经有一些标准了,比如 Time Ontology 就对时刻、时间段等信息做出了规定。另外 PROV Data Model 规定了在 RDF 中如何表示数据来源。
3.3.2 Reification
通常我们希望直接定义边本身的 context,比如 (Santiago, flight, Arica) 这个关系从 1956 年才成立。虽然我们可以用直接表示法,通过改变边的结构来加以声明,但是我们还是希望能有一种更加通用的方法来表示,这就是 Reification。
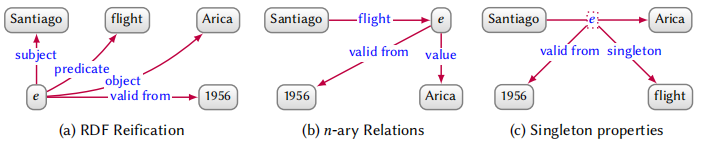
上图展示了三种 reification 方法。我们使用 $e$ 来表示任意标识符,表示可以与之关联到的边的 context 信息。(a)中定义了 $e$ 节点表示边和与之相连的节点(subject, predict, object)。(b)则是用 $e$ 代替目标节点,然后将原来的目标节点作为 $e$ 的值赋予给它。(c)用 $e$ 代替边,然后将 context 作为 $e$ 的标签。
3.3.3 Higher-arity representation
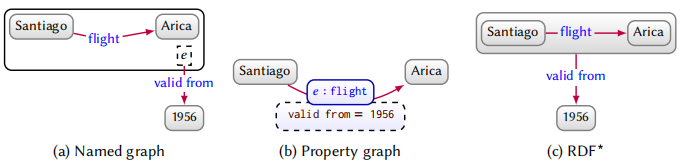
- (a)命名图的方法
- (b)属性图的方法
- (c) RDF*,RDF* 是 RDF 的扩展方法,它允许将整个三元组当成一个节点。
以上三种方法中,最灵活的就是命名图的方法。RDF* 方法是最不灵活的,比如 (Chile, president, M. Bachelet),Bachelet 担任了两届总统,2006-2010 年 和 2014-2018 年,这种情况无法用 RDF* 来描述。
3.3.4 Annotations
到目前为止我们讨论了图谱中的 context,但是还没有涉及到 context 的自动推理机制。比如假设 Santiago 到 Arica 之家只有夏季航班,我们要从 Santiago 到 Arcia 只能换一种途径。虽然直接将所有汽车、航班的日期全部表示在图谱中,或者写冗长复杂的查询语句也可以,但是这样的话可能会比较麻烦,甚至根本做不到。这个时候,我们可以考虑使用 annotations,它提供了 context 的数学定义和关键性操作符,可以帮助我们自动进行推理。
某些 annotations 是对特定领域的 context 进行建模,比如 Temporal RDF 对时间段建模:
表示 M. Bachelet 在 2006-2010 年期间担任 Chile 总统。Fuzzy RDF 对可信度进行建模:

表示 Santiago 有八成的可能性是属于 Semi-Arid 气候。
其他形式的 annotations 与领域无关,比如 Annotated RDF 允许将不同形式的 context 建模成 semi-rings:由定义域值(比如时间段)和 meet、join 两个操作符组成的代数结构:
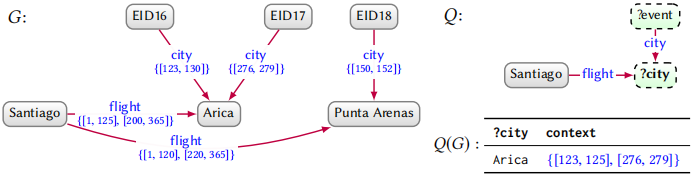
如上图所示,$G$ 表示简化的时效值集合,(1-365)表示一年的 365 天,其中形如 $\{[150,152]\}$ 表示 $\{150,151,152\}$。$Q$ 表示从 Santiago 到活动举办地的航班,返回符合时效性的答案。为了推导出答案,我们需要以下几个步骤:
- 使用 meet 操作符找到同时满足 city 和 flight 的边。比如 Santiago 和 Punta Arenas 的时效性条件分别是 $\{[150,152]\}$ 和 $\{[1,120],[220,365]\}$,两个条件的交集为空,那么这个答案就会被过滤掉。
- 使用 join 操作符,将所有符合条件的结果求并集。比如我们可以在 $\{[123, 125]\}$ 参加 EID16,在 $\{[276,279]\}$ 参加 EID17。最后将两组结果合并得到最终的 context。
3.3.5 Other Contextual framework
除了 annotations 以外,还有一些其他的模型也可以用来推理,比如 contextual knowledge repositories,允许在独立的图谱或者子图上计算 context。它不像 命名图那样,而是通过多维建模,每个图或者子图满足一个维度的条件。OnLine Analytic Processing (OLAP) 提出了基于数据块的模型,提出了 “slice-and-dice” 和 “roll-up” 等操作。更详细的内容可以参考 Contextualized Knowledge Repositories for the Semantic Web 和 Building a Conference Recommender System Based on SciGraph and WikiCFP。



