1. 前言

Dijkstra’s 是最广为人知的图算法之一，同时也是最难发音和拼写的图算法。Dijkstra’s 算法是最短路径算法，在它的基础上还衍生出很多其他变种。本文将介绍两种 Dijkstra’s 算法，并以邻接表为例用 python 实现。

Dijkstra’s 算法伪代码如下：

  1. 创建一个“距离”列表，元素个数等于图节点数。每个元素初始化无穷大；
  2. 将起始节点的“距离”设置为 0；
  3. 创建一个“访问”列表，同样将元素个数设定为图节点数。将每个元素设置成 Fasle，因为我们还没有开始访问节点；
  4. 遍历所有节点：
    • 再次遍历所有节点，然后从还没有访问的节点中挑选出距离最小的节点；
    • 将节点设置成已访问；
    • 将“距离”列表中的距离设置成相应的距离数值。
  5. 原始的“距离”列表现在应该已经包含了到每个节点的最短路径，或者如果节点无法到达的话距离为无穷大。

2. 邻接表图

假设你已经装了 numpy。

首先创建一个有 5 个节点的邻接表：

1
2
3
4
5
6
7
8
9
import numpy as np

graph = {
    0: [(1, 1)],
    1: [(0, 1), (2, 2), (3, 3)],
    2: [(1, 2), (3, 1), (4, 5)],
    3: [(1, 3), (2, 1), (4, 1)],
    4: [(2, 5), (3, 1)]
}

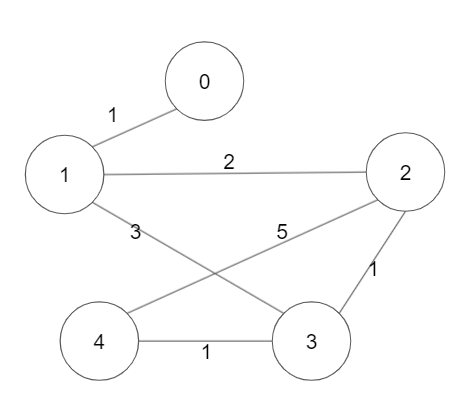
3. 用 python 实现原生 Dijkstra’s

首先先实现原生的 Dijkstra’s 算法，这种实现的算法复杂度是 $O(n^2)$。创建一个函数接收两个参数：邻接表和根节点。

首先创建一个距离列表，初始化为无穷大：

1
2
3
4
5
6
def naive_dijkstras(graph, root):
    n = len(graph)
    # 将距离列表中的所有元素初始化成无穷大
    # 这里无穷大使用的是 np.Inf，而不是设置成一个很大的数
    # 因为一个很大的数可能造成内存泄露
    dist = [np.Inf for _ in range(n)]

第二步，将根节点的距离设置成 0：

1
dist[root] = 0

第三步，创建一个“访问”列表，将所有元素初始化为 False

1
visited = [False for _ in range(n)]

第四步有三部分：

① 遍历所有节点然后挑选出距离最近的节点。如果遍历了所有的可用节点还没有找到最近的那个，那就跳出循环：

1
2
3
4
5
6
7
8
9
10
11
# 遍历所有节点
for _ in range(n):
    u = -1  # 初始节点设置成 -1
    for i in range(n):
        # 如果节点 i 还没有被访问，我们不需要对它进行处理
        # 或者如果它的距离小于 “start” 节点的时候
        if not visited[i] and (u == -1 or dist[i] < dist[u]):
            u = i
        # 访问了所有节点或者该节点无法到达
        if dist[u] == np.Inf:
            break

② 将距离最近的节点添加到“访问”列表中：

1
visited[u] = True

③ 将已访问的节点的距离设置成可用的最短距离：

1
2
3
for v, l in graph(u):
    if dist[u] + 1 < dist[v]:
        dist[v] = dist[u] + 1

最后，返回“距离”列表。

1
return dist

完整的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def naive_dijkstras(graph, root):
    n = len(graph)
    # 将距离列表中的所有元素初始化成无穷大
    # 这里无穷大使用的是 np.Inf，而不是设置成一个很大的数
    # 因为一个很大的数可能造成内存泄露
    dist = [np.Inf for _ in range(n)]
    # 将根节点的距离设置成 0
    dist[root] = 0
    # 创建一个“访问”列表，将所有元素初始化为 False
    visited = [False for _ in range(n)]
    # 遍历所有节点
    for _ in range(n):
        u = -1  # 初始节点设置成 -1
        for i in range(n):
            # 如果节点 i 还没有被访问，我们不需要对它进行处理
            # 或者如果它的距离小于 “start” 节点的时候
            if not visited[i] and (u == -1 or dist[i] < dist[u]):
                u = i
        # 访问了所有节点或者该节点无法到达
        if dist[u] == np.Inf:
            break
        # 将节点设置成已访问
        visited[u] = True
        # 将已访问的节点的距离设置成可用的最短距离
        for v, l in graph(u):
            if dist[u] + l < dist[v]:
                dist[v] = dist[u] + l
    return dist

运行上面的代码：

1
2
3
4
print(naive_dijkstras(graph,1))

# 结果为
[1, 0, 2, 3, 4]

4. 用 python 实现 Lazy Dijkstra’s

原生版的 Dijkstra’s 我们已经实现了，现在我们来尝试 Lazy Dijkstra’s。为什么叫 “Lazy Dijkstra’s”?因为我们不再遍历所有的节点（上面第四步），这样我们可以更加高效的处理稀疏图（所谓稀疏图就是并非图中的每个点都与其他点相连）。这种实现的算法复杂度是 $O(n\times\log(n))$。

假设你已经装了 heapq。

前三步和之前是一样的：

1
2
3
4
5
def lazy_dijkstras(graph, root):
    n = len(graph)
    dist = [Inf for _ in range(n)]
    dist[root] = 0
    visited = [False for _ in range(n)]

从第四步开始就与之前不同了：

首先给根节点插入一个距离 0：

1
pq = [(0, root)]

将前面第四步的①和②合并：

1
2
3
4
5
while len(pq) > 0:
    _, u = heapq.heappop(pq)
    if visited[u]:
        continue
    visited[u] = True

第四步的第三部分基本与之前一致：

1
2
3
4
for v, l in graph[u]:
    if dist[u] + l < dist[v]:
        dist[v] = dist[u] + l
        heapq.heappush(pq, (dist[v], v))

最后，返回“距离”列表。

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def lazy_dijkstras(graph, root):
    n = len(graph)
    dist = [Inf for _ in range(n)]
    dist[root] = 0
    visited = [False for _ in range(n)]
    pq = [(0, root)]
    while len(pq) > 0:
        _, u = heapq.heappop(pq)
        if visited[u]:
            continue
        visited[u] = True
        for v, l in graph[u]:
            if dist[u] + l < dist[v]:
                dist[v] = dist[u] + l
                heapq.heappush(pq, (dist[v], v))
    return dist

5. Reference

Dijkstra’s Algorithm in 5 Steps with Python

 评论