Einsum 表示法是对张量的复杂操作的一种优雅方式，本质上是使用特定领域的语言。 一旦理解并掌握了 einsum，可以帮助我们更快地编写更简洁高效的代码。

Einsum 是爱因斯坦求和（Einstein summation）的缩写，是一种求和的方法，在处理关于坐标的方程式时非常有效。在 numpy、TensorFlow 和 Pytorch 中都有相关实现，本文通过 Pytorch 实现 Transformer 中的多头注意力来介绍 einsum 在深度学习模型中的应用。

1. 矩阵乘法

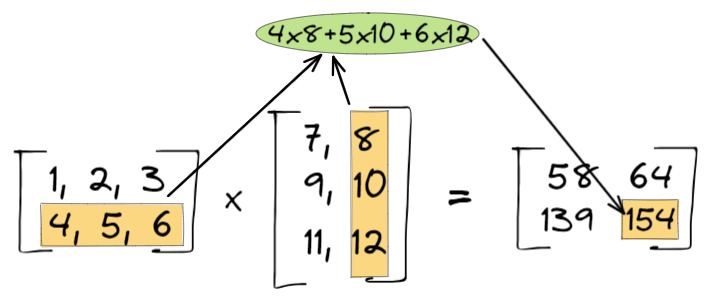
假设有两个矩阵：

我们想求两个矩阵的乘积。

  • 第一步：

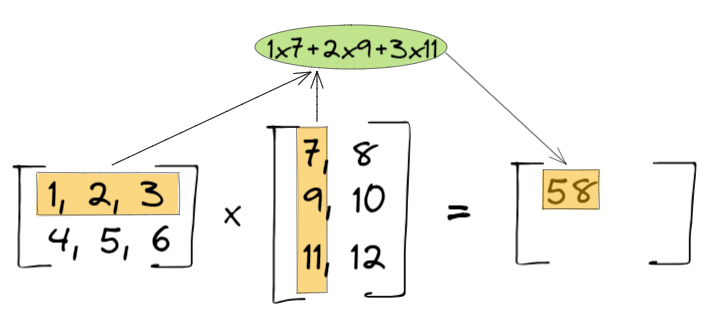
  • 第二步：

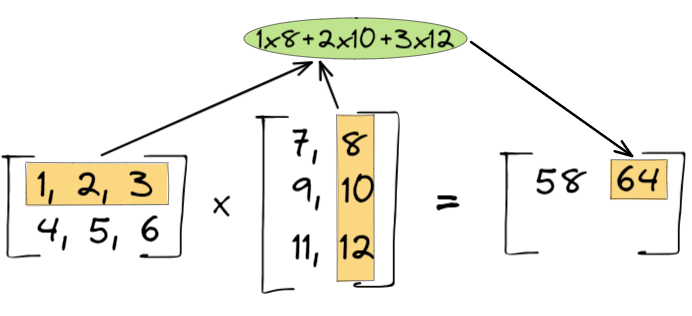
  • 第三步：

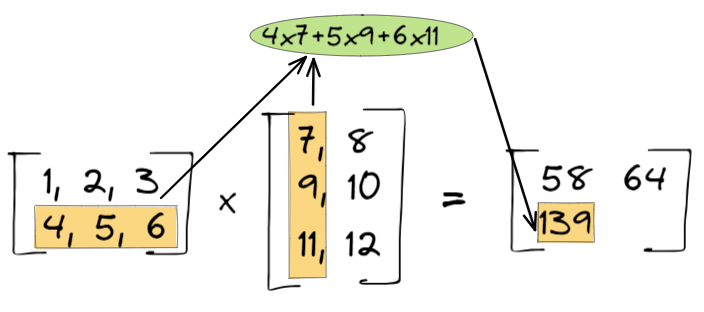
  • 第四步：

2. Einstein Notation

爱因斯坦标记法又称爱因斯坦求和约定（Einstein summation convention），基本内容是：

当两个变量具有相同的角标时，则遍历求和。在此情况下，求和号可以省略。

比如，计算两个向量的乘积， $\color{red}{a}, \color{blue}{b} \in \mathbb{R}^I$：

计算两个矩阵的乘积， $A$ $\in \mathbb{R}^{I\times K}$，$B$ $\in \mathbb{R}^{K\times J}$。用爱因斯坦求和符号表示，可以写成：

在深度学习中，通常使用的是更高阶的张量之间的变换。比如在一个 batch 中包含 $N$ 个训练样本的，最大长度是 $T$，词向量维度为 $K$ 的张量，即 $\color{red}{\mathcal{T}}\in \mathbb{R}^{N\times T \times K}$，如果想让词向量的维度映射到 $Q$ 维，则定义一个 $\color{blue}{W} \in \mathbb{R}^{K\times Q}$:

在图像处理中，通常在一个 batch 的训练样本中包含 $N$ 张图片，每张图片长为 $T$，宽为 $K$，颜色通道为 $M$，即 $\color{red}{\mathcal{T}}\in \mathbb{R}^{N\times T \times K \times M}$ 是一个 4d 张量。如果我想进行三个操作：

  • 将 $K$ 投影成 $Q$ 维；
  • 对 $T$ 进行求和；
  • 将 $M$ 和 $N$ 进行转置。

用爱因斯坦标记法可以表示成：

需要注意的是，爱因斯坦标记法是一种书写约定，是为了将复杂的公式写得更加简洁。它本身并不是某种运算符，具体运算还是要回归到各种算子上。

3. einsum

  • Numpy：np.einsum
  • Pytorch：torch.einsum
  • TensorFlow：tf.einsum

以上三种 einsum 都有相同的特性 einsum(equation, operands)：

  • equation：字符串，用来表示爱因斯坦求和标记法的；
  • operands：一些列张量，要运算的张量。

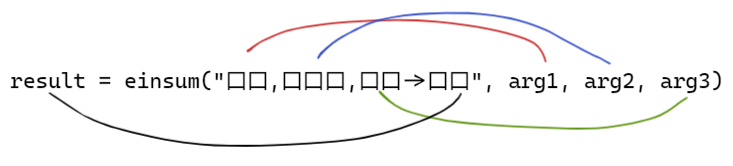
其中 口 是一个占位符，代表的是张量维度的字符。比如：

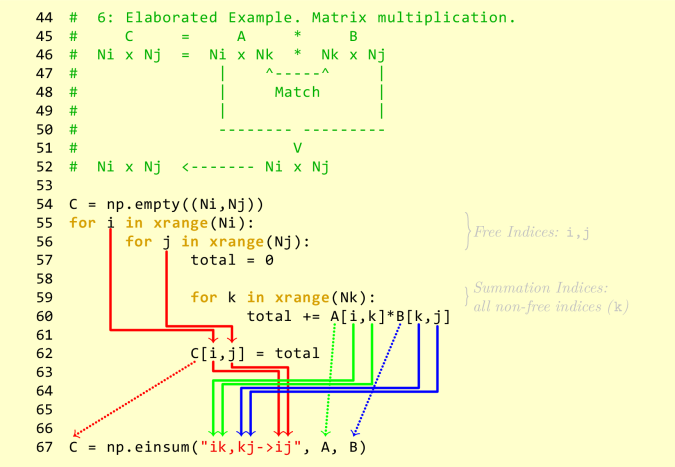
1
np.einsum('ij,jk->ik', A, B)

A 和 B 是两个矩阵，将 ij,jk->ik 分成两部分：ij, jk 和 ik，那么 ij 代表的是输入矩阵 A 的第 i 维和第 j 维，jk 代表的是 B 第 j 维和第 k 维，ik 代表的是输出矩阵的第 i 维和第 k 维。注意 i, j, k 可以是任意的字符，但是必须保持一致。换句话说，einsum 实际上是直接操作了矩阵的维度（角标）。上例中表示的是， A 和 B 的乘积。

3.1 矩阵转置

1
2
3
4
5
6
7
8
import torch
a = torch.arange(6).reshape(2, 3)
torch.einsum('ij->ji', [a])

# 输出
tensor([[ 0.,  3.],
        [ 1.,  4.],
        [ 2.,  5.]])

3.2 求和

1
2
3
4
5
a = torch.arange(6).reshape(2, 3)
torch.einsum('ij->', [a])

# 输出
tensor(15.)

3.3 列求和

1
2
3
4
5
a = torch.arange(6).reshape(2, 3)
torch.einsum('ij->j', [a])

# 输出
tensor([ 3.,  5.,  7.])

3.4 行求和

1
2
3
4
5
a = torch.arange(6).reshape(2, 3)
torch.einsum('ij->i', [a])

# 输出
tensor([  3.,  12.])

3.5 矩阵-向量乘积

1
2
3
4
5
6
a = torch.arange(6).reshape(2, 3)
b = torch.arange(3)
torch.einsum('ik,k->i', [a, b])

# 输出
tensor([  5.,  14.])

3.6 矩阵-矩阵乘积

1
2
3
4
5
6
7
a = torch.arange(6).reshape(2, 3)
b = torch.arange(15).reshape(3, 5)
torch.einsum('ik,kj->ij', [a, b])

# 输出：
tensor([[  25.,   28.,   31.,   34.,   37.],
        [  70.,   82.,   94.,  106.,  118.]])

3.7 点积

1
2
3
4
5
6
a = torch.arange(3)
b = torch.arange(3, 6)
torch.einsum('i,i->', [a, b])

# 输出：
tensor(14.)

3.8 Hardamard 积

1
2
3
4
5
6
7
a = torch.arange(6).reshape(2, 3)
b = torch.arange(6,12).reshape(2, 3)
torch.einsum('ij,ij->ij', [a, b])

# 输出：
tensor([[  0.,   7.,  16.],
        [ 27.,  40.,  55.]])

3.9 外积

1
2
3
4
5
6
7
8
a = torch.arange(3)
b = torch.arange(3, 7)
torch.einsum('i, j->ij', [a, b])

# 输出：
tensor([[  0.,   0.,   0.,   0.],
        [  3.,   4.,   5.,   6.],
        [  6.,   8.,  10.,  12.]])

3.10 Batch 矩阵乘积

1
2
3
4
5
6
7
8
9
10
11
12
13
a = torch.randn(3,2,5)
b = torch.randn(3,5,3)
torch.einsum('ijk, jkl->ijl', [a, b])

# 输出：
tensor([[[ 1.0886,  0.0214,  1.0690],
         [ 2.0626,  3.2655, -0.1465]],

        [[-6.9294,  0.7499,  1.2976],
         [ 4.2226, -4.5774, -4.8947]],

        [[-2.4289, -0.7804,  5.1385],
         [ 0.8003,  2.9425,  1.7338]]])

3.11 张量收缩

假设有两个张量 $\mathcal{A}\in \mathbb{R}^{I_1\times \dots\times I_n}$ 和 $\mathcal{B} \in \mathbb{R}^{J_1\times \dots \times J_m}$。比如 $n=4, m=5$，且 $I_2=J_3$ 和 $I_3=J_5$。我们可以计算两个张量的乘积，得到新的张量 $\mathcal{C}\in\mathbb{R}^{I_1\times I_4 \times J_1 \times J_2 \times J_4}$：

1
2
3
4
5
6
a = torch.randn(2,3,5,7)
b = torch.randn(11,13,3,17,5)
torch.einsum('pqrs,tuqvr->pstuv', [a, b]).shape

# 输出
torch.Size([2, 7, 11, 13, 17])

3.12 双线性变换

1
2
3
4
5
6
7
8
a = torch.randn(2,3)
b = torch.randn(5,3,7)
c = torch.randn(2,7)
torch.einsum('ik,jkl,il->ij', [a, b, c])

# 输出
tensor([[ 3.8471,  4.7059, -3.0674, -3.2075, -5.2435],
        [-3.5961, -5.2622, -4.1195,  5.5899,  0.4632]])

4. einops

尽管 einops 是一个通用的包，这里哦我们只介绍 einops.rearrange 。同 einsum 一样，einops.rearrange 也是操作矩阵的角标的，只不过函数的参数正好相反，如下图所示。

• NOTE
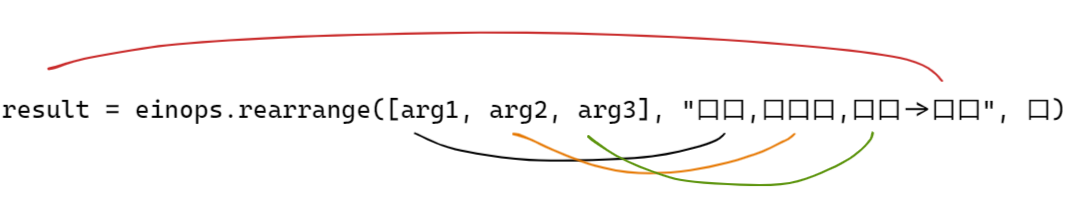
如果 rearrange 传入的参数是一个张量列表，那么后面字符串的第一维表示列表的长度。 
1
2
3
4
qkv = torch.rand(2,128,3*512) # dummy data for illustration only
# We need to decompose to n=3 tensors q, v, k
# rearrange tensor to [3, batch, tokens, dim] and cast to tuple
q, k, v = tuple(rearrange( qkv , 'b t (d n) -> n b t d ', n=3))

5. Scale dot product self-attention

  • 第一步：创建一个线性投影。给定输入 $X\in \mathbb{R}^{b\times t\times d}$，其中 $b$ 表示 $\text{batch size}$，$t$ 表示 $\text{sentence length}$，$d$ 表示 $\text{word dimension}$。

    1
    2
    3
    4
    5
    to_qvk = nn.Linear(dim, dim * 3, bias=False) # init only
    # Step 1
    qkv = to_qvk(x)  # [batch, tokens, dim*3 ]
    # decomposition to q,v,k
    q, k, v = tuple(rearrange(qkv, 'b t (d k) -> k b t d ', k=3))

  • 第二步：计算点积，mask，最后计算 softmax。

    1
    2
    3
    4
    5
    6
    7
    # Step 2
    # Resulting shape: [batch, tokens, tokens]
    scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, k) * self.scale_factor
    if mask is not None:
        assert mask.shape == scaled_dot_prod.shape[1:]
        scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)
    attention = torch.softmax(scaled_dot_prod, dim=-1)

  • 第三步：计算注意力得分与 $V$ 的乘积。

    1
    torch.einsum('b i j , b j d -> b i d', attention, v)

将上面三步综合起来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import numpy as np
import torch
from einops import rearrange
from torch import nn


class SelfAttention(nn.Module):
    """
    Implementation of plain self attention mechanism with einsum operations
    Paper: https://arxiv.org/abs/1706.03762
    Blog: https://theaisummer.com/transformer/
    """
    def __init__(self, dim):
        """
        Args:
            dim: for NLP it is the dimension of the embedding vector
            the last dimension size that will be provided in forward(x),
            where x is a 3D tensor
        """
        super().__init__()
        # for Step 1
        self.to_qvk = nn.Linear(dim, dim * 3, bias=False)
        # for Step 2
        self.scale_factor = dim ** -0.5  # 1/np.sqrt(dim)

    def forward(self, x, mask=None):
        assert x.dim() == 3, '3D tensor must be provided'

        # Step 1
        qkv = self.to_qvk(x)  # [batch, tokens, dim*3 ]

        # decomposition to q,v,k
        # rearrange tensor to [3, batch, tokens, dim] and cast to tuple
        q, k, v = tuple(rearrange(qkv, 'b t (d k) -> k b t d ', k=3))

        # Step 2
        # Resulting shape: [batch, tokens, tokens]
        scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, k) * self.scale_factor

        if mask is not None:
            assert mask.shape == scaled_dot_prod.shape[1:]
            scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)

        attention = torch.softmax(scaled_dot_prod, dim=-1)

        # Step 3
        return torch.einsum('b i j , b j d -> b i d', attention, v)

6. Multi-Head Self-Attention

  • 第一步：为每一个头创建一个线性投影 $Q, K, V$。

    1
    2
    to_qvk = nn.Linear(dim, dim_head * heads * 3, bias=False) # init only
    qkv = self.to_qvk(x)

  • 第二步：将 $Q, K, V$ 分解，并分配给每个头。

    1
    2
    3
    4
    # Step 2
    # decomposition to q,v,k and cast to tuple
    # [3, batch, heads, tokens, dim_head]
    q, k, v = tuple(rearrange(qkv, 'b t (d k h) -> k b h t d ', k=3, h=self.heads))

  • 第三步：计算注意力得分

    1
    2
    3
    4
    5
    6
    7
    # Step 3
    # resulted shape will be: [batch, heads, tokens, tokens]
    scaled_dot_prod = torch.einsum('b h i d , b h j d -> b h i j', q, k) * self.scale_factor
    if mask is not None:
        assert mask.shape == scaled_dot_prod.shape[2:]
        scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)
    attention = torch.softmax(scaled_dot_prod, dim=-1)

  • 第四步：注意力得分与 $V$ 相乘

    1
    2
    # Step 4. Calc result per batch and per head h
    out = torch.einsum('b h i j , b h j d -> b h i d', attention, v)

  • 第五步：将所有的头合并

    1
    out = rearrange(out, "b h t d -> b t (h d)")

  • 第六步：线性变换

    1
    2
    3
    self.W_0 = nn.Linear( _dim, dim, bias=False) # init only
    # Step 6. Apply final linear transformation layer
    self.W_0(out)

最终实现 MHSA：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import numpy as np
import torch
from einops import rearrange
from torch import nn


class MultiHeadSelfAttention(nn.Module):
    def __init__(self, dim, heads=8, dim_head=None):
        """
        Implementation of multi-head attention layer of the original transformer model.
        einsum and einops.rearrange is used whenever possible
        Args:
            dim: token's dimension, i.e. word embedding vector size
            heads: the number of distinct representations to learn
            dim_head: the dim of the head. In general dim_head<dim.
            However, it may not necessary be (dim/heads)
        """
        super().__init__()
        self.dim_head = (int(dim / heads)) if dim_head is None else dim_head
        _dim = self.dim_head * heads
        self.heads = heads
        self.to_qvk = nn.Linear(dim, _dim * 3, bias=False)
        self.W_0 = nn.Linear( _dim, dim, bias=False)
        self.scale_factor = self.dim_head ** -0.5

    def forward(self, x, mask=None):
        assert x.dim() == 3
        # Step 1
        qkv = self.to_qvk(x)  # [batch, tokens, dim*3*heads ]

        # Step 2
        # decomposition to q,v,k and cast to tuple
        # the resulted shape before casting to tuple will be:
        # [3, batch, heads, tokens, dim_head]
        q, k, v = tuple(rearrange(qkv, 'b t (d k h) -> k b h t d ', k=3, h=self.heads))

        # Step 3
        # resulted shape will be: [batch, heads, tokens, tokens]
        scaled_dot_prod = torch.einsum('b h i d , b h j d -> b h i j', q, k) * self.scale_factor

        if mask is not None:
            assert mask.shape == scaled_dot_prod.shape[2:]
            scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)

        attention = torch.softmax(scaled_dot_prod, dim=-1)

        # Step 4. Calc result per batch and per head h
        out = torch.einsum('b h i j , b h j d -> b h i d', attention, v)

        # Step 5. Re-compose: merge heads with dim_head d
        out = rearrange(out, "b h t d -> b t (h d)")

        # Step 6. Apply final linear transformation layer
        return self.W_0(out)

Reference

  1. Einstein Summation in Numpy, OLEXA BILANIUK

  2. A basic introduction to NumPy’s einsum, Alex Riley

  3. EINSUM IS ALL YOU NEED - EINSTEIN SUMMATION IN DEEP LEARNING, Tim Rocktäschel
  4. Understanding einsum for Deep learning: implement a transformer with multi-head self-attention from scratch, Nikolas Adaloglou
 上一页

Language Model data noising

 评论