随机梯度下降中隐式正则化的起源

首先推荐两篇论文：

• Samuel L Smith, Benoit Dherin, David Barrett, Soham De (2021) On the Origin of Implicit Regularization in Stochastic Gradient Descent
• David G.T. Barrett, Benoit Dherin (2021) Implicit Gradient Regularization

1. 深度学习为什么起作用？

为了理解为什么深度学习会如此有效，仅对损失函数或模型进行分析是不够的，这是经典泛化理论所关注的。 相反，我们用来寻找极小值的算法（即，随机梯度下降）似乎起着重要作用。 在许多任务中，强大的神经网络能够内插（interpolate）训练数据，即达到接近0的训练损失。 实际上，存在一些训练损失的最小值，它们在训练数据上几乎没有区别。 在这些最小值中，有一些也可以很好地泛化（即导致较低的测试误差），而另一些则可以任意严重地过度拟合。

那么似乎重要的不是优化算法是否迅速收敛到局部最小值，而是它希望达到那个可用的“虚拟全局”最小值。 似乎是我们用于训练深度神经网络的优化算法比其他算法更喜欢一些最小值，并且这种偏好会导致更好的泛化性能。 优化算法优先收敛到特定的最小值而避免其他最小值的情况称为隐式正则化。

2. 有限步长的影响分析

帮助我们想象深度学习模型训练过程中发生的事情的新理论之一是神经正切核（neural tangent kernels）。在这个框架下，我们研究了在无限宽层（infinitely wide layers）、全批次（full batch）和无限小学习率（ infinitesimally small learning rate）的限制下的神经网络训练。尽管这个理论有用且具有吸引力。但是使用全批、无限小学习率进行模型训练是不切实际的。实际上太小的学习率并不是总是有用的，minibatch-SGD 中梯度更新的随机性似乎也很重要。

Smith et al. (2021) 等人在的做法不同的是，他们尝试针对小型（但不是无限小的）学习率来研究minibatch-SGD，这更接近实际。 允许他们研究这种情况的工具是从微分方程的研究中借来的，称为后向误差分析（backward error analysis），无下图所示：

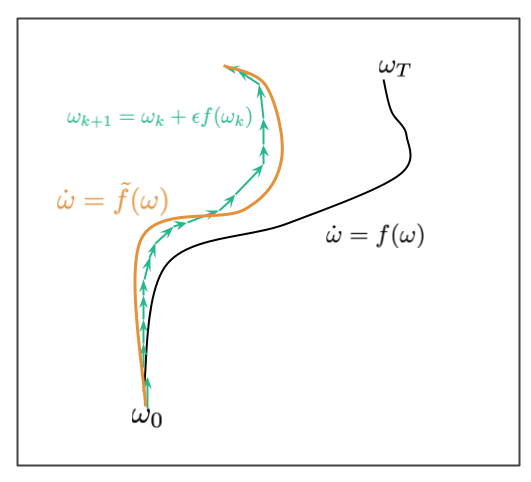
假设有一个微分方程 $\dot{\omega} = f(\omega)$，上图中黑色的曲线表示该微分方程 $\omega_t$ 的运动轨迹，初始条件为 $\omega_0$。我们通常没有办法直接进行求解，而是使用欧拉法对该微分方程进行近似：

$$\omega_{k+1} = \omega_k + \epsilon f(\omega_k)$$

这个近似是离散的，如上图绿色线所示。由于离散化带来的误差，对于有限的步长 $\epsilon$ ，离散路径可能不完全位于连续的黑色路径所在的位置。误差随着时间积累，如图所示。后向误差分析的目标是找到一个不同的微分方程 $\dot{\omega}=\widetilde f(\omega)$，使得我们找到的近似离散路径位于新的微分方程路径附近。我们的目标是对 $\widetilde{f}$ 进行反向工程使得离散化迭代能很好的用微分方程进行建模。

这个方法为什么有效？因为 $\widetilde{f}$ 采用的形式可以揭示离散化算法行为的偏好，尤其是如果它对进入不同空间有隐含偏好的话。

损失函数 $C$ 的梯度下降中，原始的微分方程是 $f(\omega)=-\nabla C(\omega)$。修正后的微分方程：

$$\dot{\omega} = - \nabla \widetilde{C}_{GD}(\omega) \\\\ \widetilde{C}_{GD}(\omega) = C(\omega)+\frac{\epsilon}{4}\lVert \nabla C(\omega)\rVert^2$$

因此，具有有限步长 $\epsilon$ 的梯度下降就像运行梯度流一样，但是增加了用来惩罚损失函数梯度的惩罚项。第二项就是所谓的隐式梯度正则化。

3. 随机梯度

在这个框架下分析 SGD 有点困难，因为随机梯度下降的轨迹是随机的。 因此，没有一个单一的要优化的离散轨迹，而是有一个不同轨迹的分布，如果要随机重排数据，则要遍历这些轨迹。如下图所示：

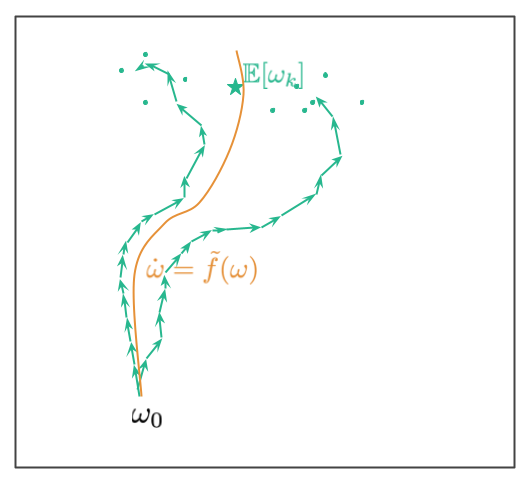
从起始点 $\omega_0$ 开始，我们有多条路径。这些路径对应于不同的数据重排的方式（论文中假设 mini-batch 中的数据是固定的，而随机性来源于 mini-batch 的处理顺序）。路径最终在一个随机位置处结束，绿色点显示了轨迹可能最终在其处的其他随机端点。 绿色星号代表了随机轨迹终点分布的平均值。

Smith et al. (2021) 的目标是对微分方程反向工程使得图中橙色的轨迹靠近绿色线的平均轨迹：

$$\dot{\omega} = - \nabla \widetilde{C}_{SGD}(\omega) \\\\ \widetilde{C}_{SGD}(\omega) = C(\omega) + \frac{\epsilon}{4m} \sum_{k=1}^{m} \lVert \nabla\hat{C}_k(\omega) \rVert^2$$

其中 $\hat{C}_k$ 表示第 $k$ 个 mini-batch 的损失函数，总共有 $m$ 个mini-batch。注意，这里与我们平时见到的梯度下降很类似，但是这里使用的是 mini-batch 梯度的平均数。另一个有趣的视角是看看 GD 和 SGD 的不同之处：

$$\widetilde{C}_{SGD} = \widetilde{C}_{GD} + \frac{\epsilon}{4m} \sum_{k=1}^m \rVert \nabla\hat{C}_k(\omega)-C(\omega) \rVert^2$$

其中额外的正则项 $\frac{\epsilon}{4m} \sum_{k=1}^m \rVert \nabla\hat{C}_k(\omega)-C(\omega) \rVert^2$，有点像 mini-batch 的总方差。直观来说，此正则化项将避免参数空间中在不同 mini-batch 上计算出的梯度变化太大。

重要的是 $C_{GD}$ 与 $C$ 有相同的最小值，但 $C_{SGD}$ 就不一定了。这就意味着，SGD 不仅与 full-batch GD 有不同的轨迹，而且可能会收敛到完全不同的解。

4. 与泛化的关系

为什么隐式正则化效果可以避免 mini-batch 梯度方差过大？ 考虑下面两个局部极小值的插图：

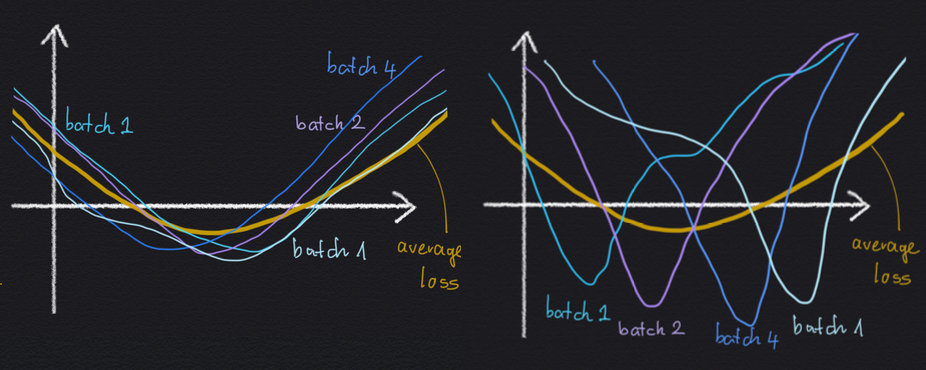
就平均损失 $C$ 来说，左右两边是相同的：最小值相同，宽度相同。但是，在左侧情况下，最小值是几个 mini-batch 损失的平均值，这些损失看起来都一样，而它们本身也相对较宽。 在右边的最小值中，宽泛的平均损失最小值是许多尖峰小批量损失的平均值，所有这些都无法确定最小值的确切位置。

可以合理地预期左边最小值可以更好地泛化，因为损失函数似乎对我们正在评估的任何特定 mini-batch 不那么敏感。这样，损失函数也可能对数据点是在训练集中还是在测试集中不太敏感。

5. 总结

总而言之，本文是对随机梯度下降的非常有趣的分析。 尽管有其局限性（作者并没有试图在本文中进行透明地隐藏和讨论），但它还是为分析有限步长优化算法提供了一种非常有趣的新技术。 论文写得很好，清楚地阐明了分析中一些乏味的细节。