1. 简介
Bengio 等人使用前馈神经网络构建语言模型,解决了两个问题:参数维度爆炸和词与词之间的语义关系的问题。然我们看到使用神经网络构建语言模型存在的巨大潜力。但是前馈神经网络构建的语言模型同样也存在问题:他只能输入特定长度的上下文(窗口 $n$)。也就是说,它只能用固定长度内的信息来预测下一个词,这与 n-gram 模型有相同的问题。
循环神经网络之前是专门用来处理序列化数据的,它对于输入长度没有限制。因此,Mikolov 等人于 2010 年提出基于 RNN 的语言模型。
2. 模型
2.1 RNN 神经网络简介

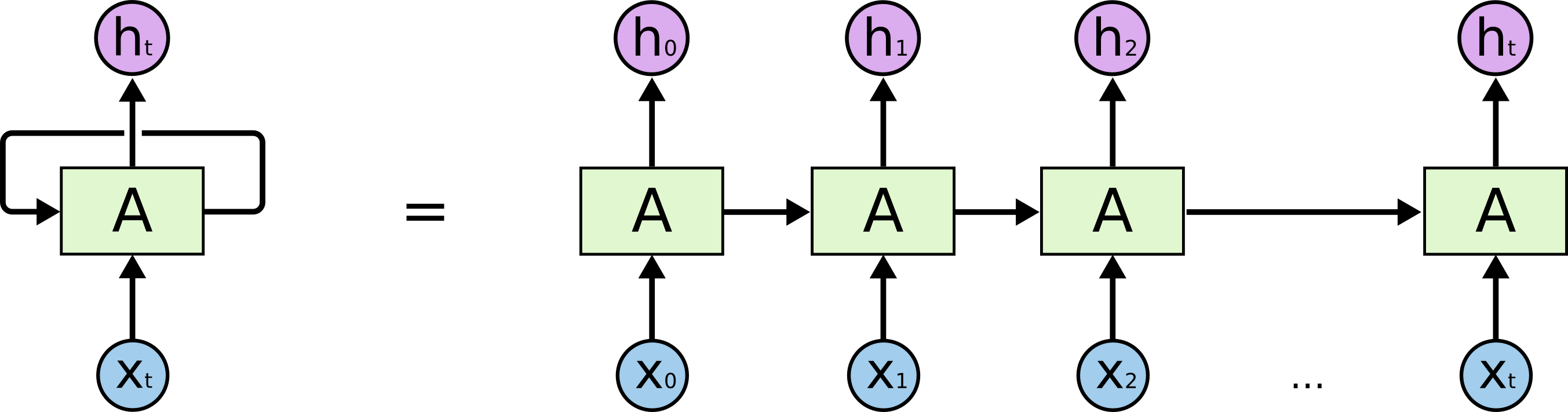
上图是一个 RNN 神经网络结构图,$A$ 是神经网络的一部分,给定输入 $x_t$,输出 $h_t$。上一步的信息通过循环传递给下一步。
循环神经网络可以看做同一个网络的多次重复,每次传递一个信息给下一级。考虑以下,我们把它展开是什么样的:
 |
 |
这个链式特性说明循环神经网络与序列和列表有很大关系。它们是用于这种序列化数据的一种很自然的网络结构。
2.2 RNN 语言模型
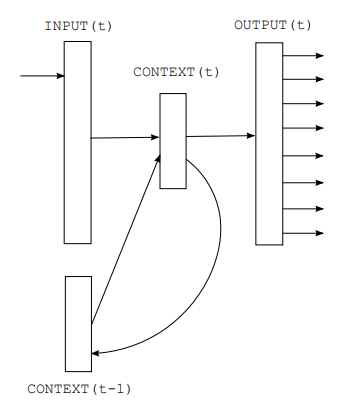
上图为模型的基本结构。该模型采用最简单的循环神经网络结构。网络分成三部分:输入层、隐藏层和输出层。
$t$ 时刻的输入层为:$t$ 时刻的词向量 $C(w_t) \in \mathbb{R}^{1\times m}$ 与 $t-1$ 时刻的隐状态 $s(t-1) \in \mathbb{R}^{1\times n}$ 向量拼接在一起的向量,即 $x(t)=[C(w_t);s(t-1)]\in \mathbb{R}^{1\times (m+n)}$;
$t$ 时刻的隐藏层为:
其中 $U\in \mathbb{R}^{(m+n)\times n}$ 表示一个权重矩阵。对于 $t=1$ 时,没有前一时刻的隐状态输出,所以需要对 $s(0)$ 进行初始化。这里采用的方法是令 $s(0)=[0.1,\cdots,0.1]^{1\times n}$,实际上只要赋值一个小量向量即可,在后续的模型更新优化过程中,初始化的向量重要性不高。
$t$ 时刻的输出层为:
其中 $W\in \mathbb{R}^{n\times |\mathcal{V}|}$ 为权重矩阵。
假设句子是:$\langle 我,爱,北京,天安门\rangle$
我们可以将模型理解为下面的过程:
- $t=1$ 时,模型输入第一个字 $w_1=我$,将它和初始化隐向量 $s(0)$ 拼在一起传递给隐藏层。然后隐藏层对输入的信息进行处理得到 $s(1)$,然后将 $s(1)$ 传递给输出层,输出层来预测句子中第 2 个词 $w_2=爱$;
- $t=2$ 时,模型输入第二个字 $w_2=爱$,将它和上一步得到的隐向量 $s(1)$ 拼在一起传递给隐藏层。然后隐藏层对输入的信息进行处理得到 $s(2)$,然后将 $s(2)$ 传递给输出层,输出层来预测句子中第 3 个词 $w_3=北京$;
$t=3$ 时,模型输入第二个字 $w_3=北京$,将它和上一步得到的隐向量 $s(2 )$ 拼在一起传递给隐藏层。然后隐藏层对输入的信息进行处理得到 $s(3)$,然后将 $s(3)$ 传递给输出层,输出层来预测句子中第 4 个词 $w_4=天安门$;
模型的每一步都将前面接受到的所有信息存储在隐藏状态里了,输出层是利用之前所有序列产生的隐藏状态来预测下一个词。这样就避免了前馈神经网络那样只能使用固定长度内的信息来预测下一个词。
损失函数定义为:
其中 $d(t)$ 表示第 $t$ 步真实的词,$y(t)$ 表示模型输出的词。
作者还提出一个动态模型的概念:在测试阶段也要更新模型。作者认为在训练阶段同一批数据会多次更新参数,而经过多轮训练以后,再进行一次测试集的参数更新对模型本身影响不大,但是可能会提升某些不常见的句子的表现。比如训练集中经常出现 ”狗“ 的句子,但是很少出现 ”猫“,而在测试集中有 “猫”的类似的句子,这种情况下,使用动态模型可能会提升模型应对不常见句子的能力。
3. 模型优化
为了提升模型的表现,将所有出现频率低于某一阈值的词全部替换成统一的编码,比如 $
其中 $C_{
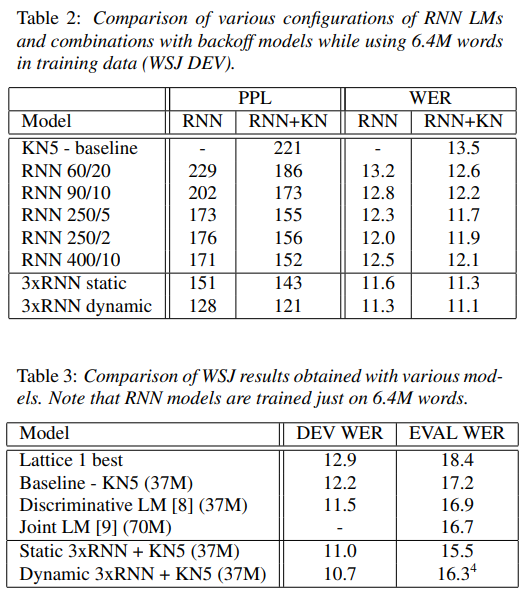
4. 实验结果
5. 总结
基于 RNN 的语言模型解决了前馈神经网络语言模型的视野太短问题,但是由于 RNN 本身的梯度消失问题导致实际上语言模型能够建模的序列长度也是有限的。
6. Reference
Recurrent neural network based language model. Tomas Mikolov , Martin Karafiat , Lukas Burget , Jan Honza Cernocky , Sanjeev Khudanpur, 2010



