文章转载自:模型压缩 | 知识蒸馏经典解读 。
知识蒸馏是一种模型压缩方法,是一种基于“教师-学生网络思想”的训练方法,由于其简单,有效,在工业界被广泛应用。这一技术的理论来自于2015年Hinton发表的一篇神作:Distilling the Knowledge in a Neural Network
Knowledge Distillation,简称KD,顾名思义,就是将已经训练好的模型包含的知识(”Knowledge”),蒸馏(“Distill”)提取到另一个模型里面去。今天,我们就来简单读一下这篇论文,力求用简单的语言描述论文作者的主要思想。在本文中,我们将从背景和动机讲起,然后着重介绍“知识蒸馏”的方法,最后我会讨论“温度“这个名词:
「温度」 : 我们都知道“蒸馏”需要在高温下进行,那么这个“蒸馏”的温度代表了什么,又是如何选取合适的温度?
背景 虽然在一般情况下,我们不会去区分训练和部署使用的模型,但是训练和部署之间存在着一定的不一致性:
在训练过程中,我们需要使用复杂的模型,大量的计算资源,以便从非常大、高度冗余的数据集中提取出信息。在实验中,效果最好的模型往往规模很大,甚至由多个模型集成得到。而大模型不方便部署到服务中去,常见的瓶颈如下:
在部署时,我们对延迟以及计算资源都有着严格的限制。
因此,模型压缩(在保证性能的前提下减少模型的参数量)成为了一个重要的问题。而「模型蒸馏」 属于模型压缩的一种方法。
“思想歧路” 人们在直觉上会觉得,要保留相近的知识量,必须保留相近规模的模型。也就是说,一个模型的参数量基本决定了其所能捕获到的数据内蕴含的“知识”的量。
这样的想法是基本正确的,但是需要注意的是:
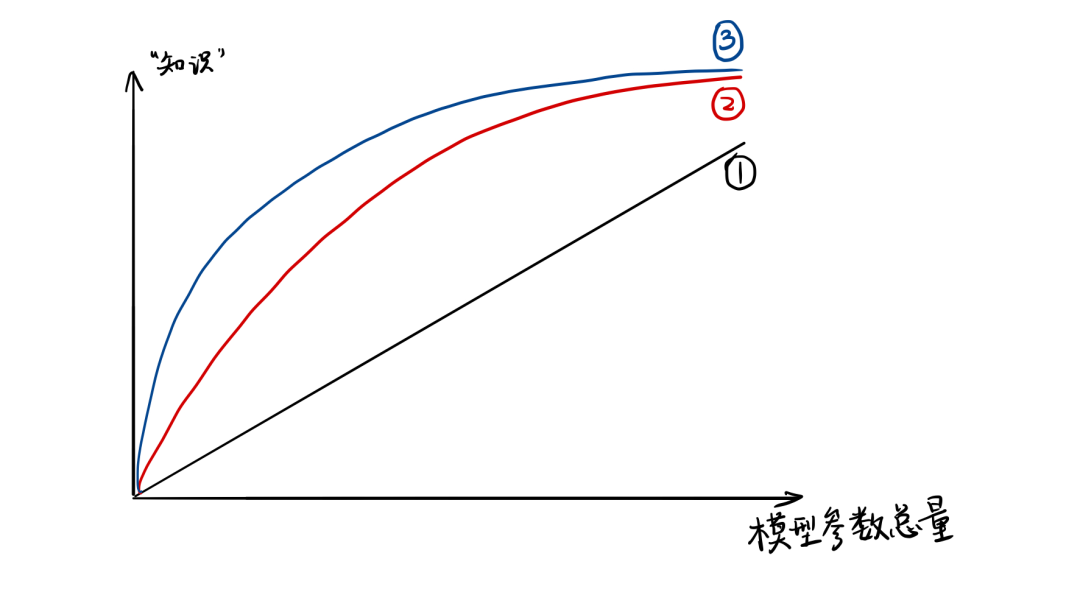
模型的参数量和其所能捕获的“知识“量之间并非稳定的线性关系(下图中的1),而是接近边际收益逐渐减少的一种增长曲线(下图中的2和3)。
完全相同的模型架构和模型参数量,使用完全相同的训练数据,能捕获的“知识”量并不一定完全相同,另一个关键因素是训练的方法。合适的训练方法可以使得在模型参数总量比较小时,尽可能地获取到更多的“知识”(下图中的3与2曲线的对比)。
知识蒸馏的理论依据 Teacher Model 和 Student Model 知识蒸馏使用的是Teacher—Student模型,其中teacher是“知识”的输出者,student是“知识”的接受者。知识蒸馏的过程分为2个阶段:
原始模型训练: 训练”Teacher模型”, 简称为Net-T,它的特点是模型相对复杂,也可以由多个分别训练的模型集成而成。我们对”Teacher模型”不作任何关于模型架构、参数量、是否集成方面的限制,唯一的要求就是,对于输入X, 其都能输出Y,其中Y经过softmax的映射,输出值对应相应类别的概率值。
精简模型训练: 训练”Student模型”, 简称为Net-S,它是参数量较小、模型结构相对简单的单模型。同样的,对于输入X,其都能输出Y,Y经过softmax映射后同样能输出对应相应类别的概率值。
在本论文中,作者将问题限定在「分类问题」 下,或者其他本质上属于分类问题的问题,该类问题的共同点是模型最后会有一个softmax层,其输出值对应了相应类别的概率值。
知识蒸馏的关键点 如果回归机器学习最最基础的理论,我们可以很清楚地意识到一点(而这一点往往在我们深入研究机器学习之后被忽略): 机器学习「最根本的目的」 在于训练出在某个问题上泛化能力强的模型。
泛化能力强: 在某问题的所有数据上都能很好地反应输入和输出之间的关系,无论是训练数据,还是测试数据,还是任何属于该问题的未知数据。
而现实中,由于我们不可能收集到某问题的所有数据来作为训练数据,并且新数据总是在源源不断的产生,因此我们只能退而求其次,训练目标变成在已有的训练数据集上建模输入和输出之间的关系。由于训练数据集是对真实数据分布情况的采样,训练数据集上的最优解往往会多少偏离真正的最优解(这里的讨论不考虑模型容量)。
而在知识蒸馏时,由于我们已经有了一个泛化能力较强的Net-T,我们在利用Net-T来蒸馏训练Net-S时,可以直接让Net-S去学习Net-T的泛化能力。
一个很直白且高效的迁移泛化能力的方法就是使用 softmax 层输出的类别的概率来作为 “soft target”。
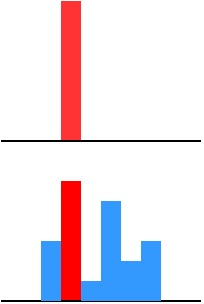
传统 training 过程 (hard targets): 对 ground truth 求极大似然。
KD 的 training 过程(soft targets): 用 large model 的 class probabilities 作为 soft targets。
为什么? softmax 层的输出,除了正例之外,负标签也带有大量的信息,比如某些负标签对应的概率远远大于其他负标签。而在传统的训练过程 (hard target) 中,所有负标签都被统一对待。也就是说,KD的训练方式使得每个样本给Net-S带来的信息量大于传统的训练方式。
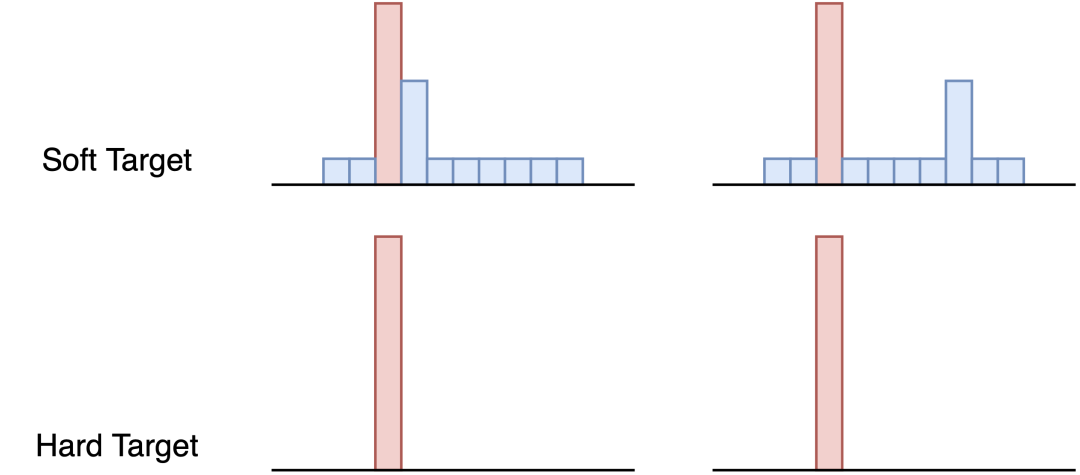
举个例子来说明一下: 在手写体数字识别任务 MNIST 中,输出类别有10个。
假设某个输入的“2”更加形似”3”,softmax 的输出值中”3”对应的概率为0.1,而其他负标签对应的值都很小,而另一个”2”更加形似”7”,”7”对应的概率为0.1。这两个”2”对应的hard target的值是相同的,但是它们的soft target却是不同的,由此我们可见soft target蕴含着比hard target多的信息。并且soft target分布的熵相对高时,其soft target蕴含的知识就更丰富。
这就解释了为什么通过蒸馏的方法训练出的 Net-S 相比使用完全相同的模型结构和训练数据只使用 hard target 的训练方法得到的模型,拥有更好的泛化能力。
softmax 函数 先回顾一下原始的 softmax 函数:
但要是直接使用 softmax 层的输出值作为 soft target,这又会带来一个问题: 当 softmax 输出的概率分布熵相对较小时,负标签的值都很接近 0,对损失函数的贡献非常小,小到可以忽略不计。因此”温度”这个变量就派上了用场。
下面的公式时加了温度这个变量之后的 softmax 函数:
这里的 $T$ 就是「温度」 。
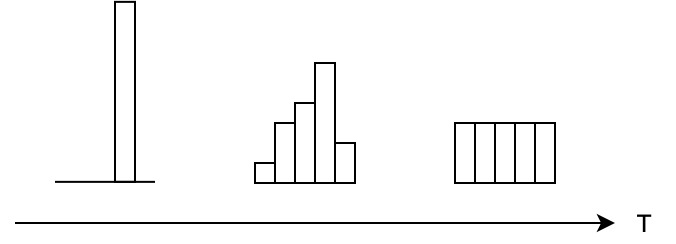
原来的 softmax 函数是 $T = 1$ 的特例。$T$ 越高,softmax 的概率分布越趋于平滑,其分布的熵越大,负标签携带的信息会被相对地放大,模型训练将更加关注负标签。
知识蒸馏的具体方法 通用的知识蒸馏方法
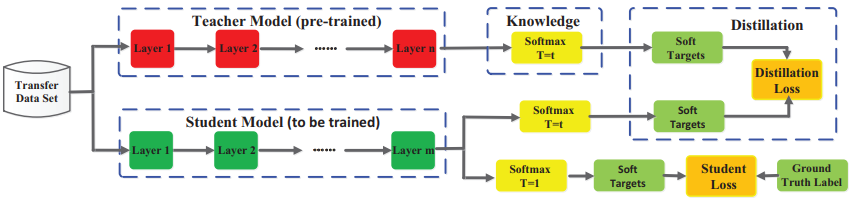
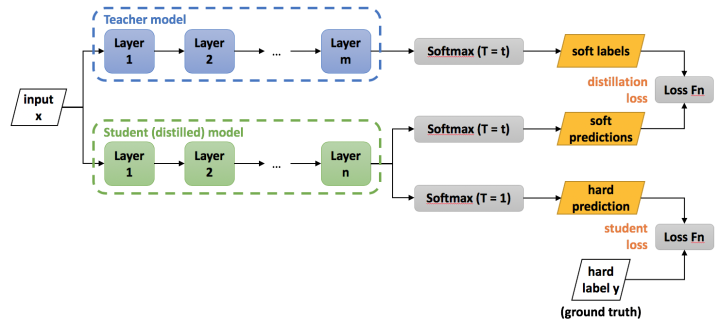
第一步是训练 Net-T;第二步是在高温 $T$ 下,蒸馏 Net-T 的知识到 Net-S。训练 Net-T 的过程很简单,下面详细讲讲第二步:高温蒸馏的过程。高温蒸馏过程的目标函数由 distill loss (对应soft target) 和 student loss (对应 hard target)加权得到,示意图如上。
Net-T 和 Net-S 同时输如训练集, 用 Net-T 输出概率来作为 soft target,Net-S 在相同温度 $T$ 下的 softmax 输出和 soft target 的 cross entropy 就是「Loss函数的第一部分」 $L_{\text{soft}}$:
其中 $p_i^T=\frac{\exp(v_i/T)}{\sum_k^N \exp(v_k/T)}$,$q_i^T=\frac{\exp(z_i/T)}{\sum_k^N \log(z_k/T)}$。
Net-S 在 $T=1$下的 softmax 输出和 ground truth 的 cross entropy 就是「Loss函数的第二部分」 $L_{\text{hard}}$:
其中,$c_j$ 表示在第 $j$ 类上的 ground truth 值,$c_j \in \{0,1\}$, 正标签取 1,负标签取 0。$q_j^1=\frac{\exp(z_i)}{\sum_j^N \exp(z_j)}$。
第二部分 $L_{\text{hard}}$ 的必要性其实很好理解: Net-T 也有一定的错误率,使用 ground truth 可以有效降低错误被传播给 Net-S 的可能。打个比方,老师虽然学识远远超过学生,但是他仍然有出错的可能,而这时候如果学生在老师的教授之外,可以同时参考到标准答案,就可以有效地降低被老师偶尔的错误“带偏”的可能性。
一种特殊情形: 直接match logits(不经过softmax) 直接 match logits 指的是,直接使用 softmax 层的输入 logits(而不是输出)作为 soft targets,需要最小化的目标函数是 Net-T 和 Net-S 的 logits 之间的平方差。
由单个 case 贡献的 loss,推算出对应在 Net-S 每个 logit $z_i$上的梯度:
当 $T \rightarrow \infty$ 时,$e^{x/T} \rightarrow 1 + x/T$ ,于是:
假设 logits 是零均值的,即 $\sum_j z_j = \sum_j v_j=0$,则
也就是相当于最小化:
关于”温度”的讨论 【问题】 我们都知道“蒸馏”需要在高温下进行,那么这个“蒸馏”的温度代表了什么,又是如何选取合适的温度?
温度的特点 在回答这个问题之前,先讨论一下「温度T的特点」
原始的softmax函数是 时的特例, 时,概率分布比原始更“陡峭”, 时,概率分布比原始更“平缓”。
温度越高,softmax上各个值的分布就越平均(思考极端情况: (i), 此时softmax的值是平均分布的;(ii) ,此时softmax的值就相当于,即最大的概率处的值趋近于1,而其他值趋近于0)
不管温度T怎么取值,Soft target都有忽略小的 携带的信息的倾向
温度代表了什么,如何选取合适的温度? 温度的高低改变的是Net-S训练过程中对负标签的关注程度: 温度较低时,对负标签的关注,尤其是那些显著低于平均值的负标签的关注较少;而温度较高时,负标签相关的值会相对增大,Net-S会相对多地关注到负标签。
实际上,负标签中包含一定的信息,尤其是那些值显著「高于」 平均值的负标签。但由于Net-T的训练过程决定了负标签部分比较noisy,并且负标签的值越低,其信息就越不可靠。因此温度的选取比较empirical,本质上就是在下面两件事之中取舍:
从有部分信息量的负标签中学习 –> 温度要高一些
防止受负标签中噪声的影响 –> 温度要低一些
总的来说,$T$ 的选择和 Net-S 的大小有关,Net-S 参数量比较小的时候,相对比较低的温度就可以了(因为参数量小的模型不能 capture all knowledge,所以可以适当忽略掉一些负标签的信息)
实例 下面我们用一个图像分类器举个例子。
1 2 3 4 5 6 7 8 9 10 11 12 import tensorflow as tftf.random.set_seed(666 ) from tensorflow.keras.applications import MobileNetV2from tensorflow.keras import modelsfrom tensorflow.keras import layersimport tensorflow_datasets as tfdstfds.disable_progress_bar() import matplotlib.pyplot as plt
1 2 3 4 5 6 train_ds, validation_ds = tfds.load( "tf_flowers" , split=["train[:85%]" , "train[85%:]" ], as_supervised=True )
1 2 3 4 5 6 7 8 plt.figure(figsize=(10 , 10 )) for i, (image, label) in enumerate(train_ds.take(9 )): ax = plt.subplot(3 , 3 , i + 1 ) plt.imshow(image) plt.title(int(label)) plt.axis("off" )
1 2 3 4 5 6 7 8 SIZE = (224 , 224 ) def preprocess_image (image, label) : image = tf.image.convert_image_dtype(image, tf.float32) image = tf.image.resize(image, SIZE) return (image, label)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 BATCH_SIZE = 64 AUTO = tf.data.experimental.AUTOTUNE train_ds = ( train_ds .map(preprocess_image, num_parallel_calls=AUTO) .cache() .shuffle(1024 ) .batch(BATCH_SIZE) .prefetch(buffer_size=tf.data.experimental.AUTOTUNE) ) validation_ds = ( validation_ds .map(preprocess_image, num_parallel_calls=AUTO) .cache() .batch(BATCH_SIZE) .prefetch(buffer_size=tf.data.experimental.AUTOTUNE) )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 base_model = MobileNetV2(weights="imagenet" , include_top=False , input_shape=(224 , 224 , 3 )) base_model.trainable = True def get_teacher_model () : inputs = layers.Input(shape=(224 , 224 , 3 )) x = base_model(inputs, training=False ) x = layers.GlobalAveragePooling2D()(x) x = layers.Dense(5 )(x) classifier = models.Model(inputs=inputs, outputs=x) return classifier get_teacher_model().summary()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Model: "functional_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_2 (InputLayer) [(None, 224, 224, 3)] 0 _________________________________________________________________ mobilenetv2_1.00_224 (Functi (None, 7, 7, 1280) 2257984 _________________________________________________________________ global_average_pooling2d (Gl (None, 1280) 0 _________________________________________________________________ dense (Dense) (None, 5) 6405 ================================================================= Total params: 2,264,389 Trainable params: 2,230,277 Non-trainable params: 34,112 _________________________________________________________________
1 2 3 loss_func = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True ) optimizer = tf.keras.optimizers.Adam(learning_rate=1e-5 )
1 2 3 4 5 6 teacher_model = get_teacher_model() teacher_model.compile(loss=loss_func, optimizer=optimizer, metrics=["accuracy" ]) teacher_model.fit(train_ds, validation_data=validation_ds, epochs=5 )
1 2 3 4 5 6 7 8 9 10 11 12 13 Epoch 1/5 2/Unknown - 0s 245ms/step - loss: 1.6895 - accuracy: 0.2969WARNING:tensorflow:Callbacks method `on_train_batch_end` is slow compared to the batch time (batch time: 0.1600s vs `on_train_batch_end` time: 0.3296s). Check your callbacks. WARNING:tensorflow:Callbacks method `on_train_batch_end` is slow compared to the batch time (batch time: 0.1600s vs `on_train_batch_end` time: 0.3296s). Check your callbacks. 49/49 [==============================] - 24s 490ms/step - loss: 0.9725 - accuracy: 0.6224 - val_loss: 0.5764 - val_accuracy: 0.8000 Epoch 2/5 49/49 [==============================] - 22s 456ms/step - loss: 0.4474 - accuracy: 0.8449 - val_loss: 0.3946 - val_accuracy: 0.8655 Epoch 3/5 49/49 [==============================] - 23s 463ms/step - loss: 0.3020 - accuracy: 0.9006 - val_loss: 0.3256 - val_accuracy: 0.8782 Epoch 4/5 49/49 [==============================] - 23s 466ms/step - loss: 0.2312 - accuracy: 0.9282 - val_loss: 0.2882 - val_accuracy: 0.8982 Epoch 5/5 49/49 [==============================] - 22s 456ms/step - loss: 0.1779 - accuracy: 0.9446 - val_loss: 0.2606 - val_accuracy: 0.9145 <tensorflow.python.keras.callbacks.History at 0x7ff81abec8d0>
1 2 3 print("Test accuracy: {:.2f}" .format(teacher_model.evaluate(validation_ds)[1 ]*100 )) teacher_model.save_weights("teacher_model.h5" )
1 2 9/9 [==============================] - 1s 67ms/step - loss: 0.2606 - accuracy: 0.9145 Test accuracy: 91.45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 def get_student_model (deeper=False) : student_model = models.Sequential() student_model.add(layers.Conv2D(64 , (3 , 3 ), input_shape=(224 , 224 , 3 ), activation="relu" , kernel_initializer="he_normal" )) student_model.add(layers.MaxPooling2D((4 , 4 ))) student_model.add(layers.Conv2D(128 , (3 , 3 ), activation="relu" , kernel_initializer="he_normal" )) if deeper: student_model.add(tf.keras.layers.MaxPooling2D((4 , 4 ))) student_model.add(tf.keras.layers.Conv2D(256 , (3 , 3 ), activation="relu" , kernel_initializer="he_normal" )) student_model.add(layers.GlobalAveragePooling2D()) student_model.add(layers.Dense(512 , activation='relu' )) student_model.add(layers.Dense(5 )) return student_model get_student_model().summary()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d (Conv2D) (None, 222, 222, 64) 1792 _________________________________________________________________ max_pooling2d (MaxPooling2D) (None, 55, 55, 64) 0 _________________________________________________________________ conv2d_1 (Conv2D) (None, 53, 53, 128) 73856 _________________________________________________________________ global_average_pooling2d_2 ( (None, 128) 0 _________________________________________________________________ dense_2 (Dense) (None, 512) 66048 _________________________________________________________________ dense_3 (Dense) (None, 5) 2565 ================================================================= Total params: 144,261 Trainable params: 144,261 Non-trainable params: 0
1 2 3 4 5 6 7 train_loss = tf.keras.metrics.Mean(name="train_loss" ) valid_loss = tf.keras.metrics.Mean(name="test_loss" ) train_acc = tf.keras.metrics.SparseCategoricalAccuracy(name="train_acc" ) valid_acc = tf.keras.metrics.SparseCategoricalAccuracy(name="valid_acc" )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 def get_kd_loss ( student_logits, teacher_logits, true_labels, temperature, alpha, beta ) : teacher_probs = tf.nn.softmax(teacher_logits / temperature) kd_loss = tf.keras.losses.categorical_crossentropy( teacher_probs, student_logits / temperature, from_logits=True ) ce_loss = tf.keras.losses.sparse_categorical_crossentropy( true_labels, student_logits, from_logits=True ) total_loss = (alpha * kd_loss) + (beta * ce_loss) return total_loss / (alpha + beta) class Student (tf.keras.Model) : def __init__ ( self, trained_teacher, student, temperature=5. , alpha=0.9 , beta=0.1 ) : super(Student, self).__init__() self.trained_teacher = trained_teacher self.student = student self.temperature = temperature self.alpha = alpha self.beta = beta def train_step (self, data) : images, labels = data teacher_logits = self.trained_teacher(images) with tf.GradientTape() as tape: student_logits = self.student(images) loss = get_kd_loss(student_logits, teacher_logits, labels, self.temperature, self.alpha, self.beta) gradients = tape.gradient(loss, self.student.trainable_variables) gradients = [gradient * (self.temperature ** 2 ) for gradient in gradients] self.optimizer.apply_gradients(zip(gradients, self.student.trainable_variables)) train_loss.update_state(loss) train_acc.update_state(labels, tf.nn.softmax(student_logits)) t_loss, t_acc = train_loss.result(), train_acc.result() train_loss.reset_states(), train_acc.reset_states() return {"train_loss" : t_loss, "train_accuracy" : t_acc} def test_step (self, data) : images, labels = data teacher_logits = self.trained_teacher(images) student_logits = self.student(images, training=False ) loss = get_kd_loss(student_logits, teacher_logits, labels, self.temperature, self.alpha, self.beta) valid_loss.update_state(loss) valid_acc.update_state(labels, tf.nn.softmax(student_logits)) v_loss, v_acc = valid_loss.result(), valid_acc.result() valid_loss.reset_states(), valid_acc.reset_states() return {"loss" : v_loss, "accuracy" : v_acc}
1 2 3 4 5 6 7 student = Student(teacher_model, get_student_model()) optimizer = tf.keras.optimizers.Adam(learning_rate=0.01 ) student.compile(optimizer) student.fit(train_ds, validation_data=validation_ds, epochs=10 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Epoch 1/10 49/49 [==============================] - 9s 183ms/step - train_loss: 1.5737 - train_accuracy: 0.3676 - val_loss: 1.5175 - val_accuracy: 0.5526 Epoch 2/10 49/49 [==============================] - 8s 162ms/step - train_loss: 1.4912 - train_accuracy: 0.4995 - val_loss: 1.5057 - val_accuracy: 0.5000 Epoch 3/10 49/49 [==============================] - 8s 163ms/step - train_loss: 1.4781 - train_accuracy: 0.5353 - val_loss: 1.4710 - val_accuracy: 0.5789 Epoch 4/10 49/49 [==============================] - 8s 162ms/step - train_loss: 1.4695 - train_accuracy: 0.5513 - val_loss: 1.5139 - val_accuracy: 0.5263 Epoch 5/10 49/49 [==============================] - 8s 161ms/step - train_loss: 1.4600 - train_accuracy: 0.5866 - val_loss: 1.4609 - val_accuracy: 0.6316 Epoch 6/10 49/49 [==============================] - 8s 161ms/step - train_loss: 1.4436 - train_accuracy: 0.6128 - val_loss: 1.4620 - val_accuracy: 0.5789 Epoch 7/10 49/49 [==============================] - 8s 161ms/step - train_loss: 1.4367 - train_accuracy: 0.6258 - val_loss: 1.4253 - val_accuracy: 0.7105 Epoch 8/10 49/49 [==============================] - 8s 161ms/step - train_loss: 1.4337 - train_accuracy: 0.6344 - val_loss: 1.4406 - val_accuracy: 0.6579 Epoch 9/10 49/49 [==============================] - 8s 160ms/step - train_loss: 1.4210 - train_accuracy: 0.6578 - val_loss: 1.4136 - val_accuracy: 0.7105 Epoch 10/10 49/49 [==============================] - 8s 160ms/step - train_loss: 1.4085 - train_accuracy: 0.6797 - val_loss: 1.4602 - val_accuracy: 0.5789 <tensorflow.python.keras.callbacks.History at 0x7ff823b11b00>