Transformer家族之Deep Transformer

Transformer 的功能强大已经是学术界的共识，但是它难以训练也是有目共睹的。本身的巨大参数量已经给训练带来了挑战，如果我们想再加深深度可谓难上加难。这篇文章将会介绍几篇就如何加深 Transformer 的展开研究论文。从目前的研究来看 Transformer 之所以难训是由于梯度消失的问题，要对 Transformer 进行加深就必须要解决这个问题，今天我们介绍三种方法：

• Depth-Scaled Initialization
• Lipschitz Constrained Parameter Initialization
• Pre-Norm

1. Vanishing Gradient Analysis

从目前的研究来看，影响 Transformer 收敛的主要因素是残差连接和 LayerNorm 部分的梯度消失问题，比如 Chen et al. (2018) ，Zhang et al. (2019)，Wang et al. (2019)，Xiong et al. (2020) 的研究都证实了这一假设。

Transformer 残差连接和 LayerNorm 如下：

$$y_l = x_l+\mathcal{F}(x_l;\theta) \\\\ x_{l+1} = \mathrm{LayerNorm}(y_l)$$

令 $\mathcal{E}$ 表示损失，$x_L$ 表示顶层 sub-layer 的输出，根据链式法则有：

$$\frac{\partial\mathcal{E}}{\partial x_l} = \frac{\partial \mathcal{E}}{\partial x_L} \frac{\partial x_L}{\partial x_l}$$

一层一层分解得：

$$\frac{\partial x_L}{\partial x_l} = \frac{\partial x_L}{\partial x_{L-1}} \frac{\partial x_{L-1}}{\partial x_{L-2}} \cdots \frac{\partial x_{l+1}}{\partial x_l}$$

将 $x_{l+1}$ 表达式代入得：

$$\frac{\partial x_{l+1}}{\partial x_l} = \frac{\partial x_{l+1}}{\partial y_l}\frac{\partial y_l}{\partial x_l}=\frac{\partial \mathrm{LayerNorm}(y_l)}{\partial y_l}\left(1 + \frac{\partial \mathcal{F}(x_l;\theta_l)}{\partial x_l}\right)$$

因此，我们可以得到：

$$\frac{\partial \mathcal{E}}{\partial x_l} = \frac{\mathcal{E}}{\partial x_L} \times \prod_{k=l}^{L-1}\left[\frac{\partial \mathrm{LayerNorm(y_k)}}{\partial y_k}\left(1+\frac{\partial \mathcal{F}(x_k;\theta_k)}{\partial x_k}\right) \right]$$

从上面的分析可以看出，损失函数在先后传播的时候是连乘形式的，这样很容易出现梯度消失或者梯度爆炸问题。另外，Xiong et al. (2020) 进一步证明随着损失梯度的向后传播的深度，其大小是以 $(2/3)^{L-l}$ 指数形式下降的。

实验上，下面两张图分别是 Zhang et al. (2019) 和 Xiong et al. (2020) 的独立实验结果。上图我们只看实线部分，下图只看橙色柱状图。我们会发现，实验结果所展示出来的原始的 Transformer 中损失梯度随层数的变化趋势和理论分析基本一致。因此，我们可以认为之前的理论分析是合理的。

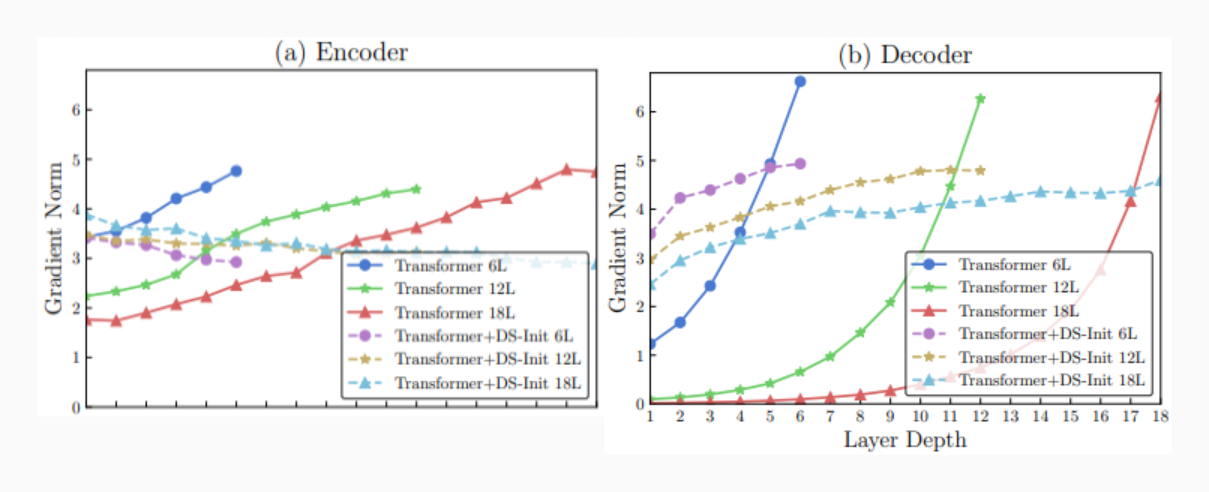
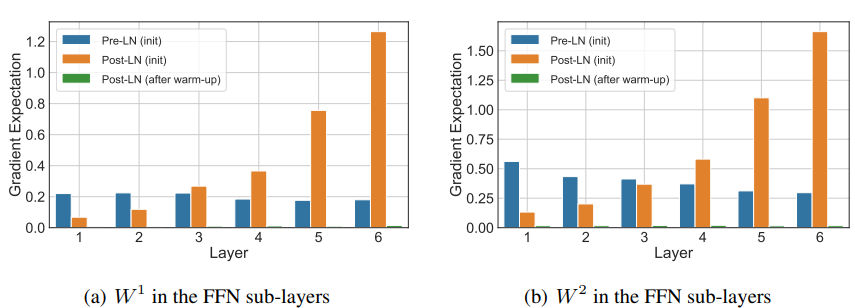
现在，我们知道 Transformer 梯度消失之谜了，接下来我们就可以针对这个问题提出解决方案了。

2. Depth-Scaled Initialization and Merged Attention

2.1 Depth-Scaled Initialization

Zhang 等人将 Transformer 的梯度消失问题归咎于残差连接输出的方差过大（方差过大会造成梯度消失可参考自注意力为什么scaled 的相关讨论）。

传统的 Transformer 所有参数都是通过均匀分布随机采样初始化的：

$$\mathbf{W} \in \mathbb{R}^{d_i \times d_o} \sim \mathcal{U}(-\gamma, \gamma) \\\\ \gamma = \sqrt{\frac{6}{d_i + d_o}}$$

其中 $d_i$ 和 $d_o$ 分别表示输入和输出的维度。

作者定义了误差信号的变化比率 $\beta$ 来表示在传播过程中误差信号是增强还是减弱。$\beta = \beta_{RC}\cdot \beta_{LN}$，其中 $\beta_{RC}$ 和 $\beta_{LN}$ 分别表示残差连接和 LayerNorm 对误差信号的影响。为了保证训练过程的稳定，理论上我们应该尽量让 $\beta$ 保持在 $\beta \approx 1$。通过实验发现 LayerNorm 会削弱信号 $\beta_{LN} \lt 1$，残差连接会增强信号 $\beta_{RC} \gt 1$，并且而削弱的强度小于增强的强度，也就是说最终会导致 $\beta \gt 1$。

为了避免这种情况发生，作者提出一种新的初始化方法 —— DS-Init：

$$\mathbf{W} \in \mathbb{R}^{d_i \times d_o} \sim \mathcal{U}(-\gamma \frac{\alpha}{\sqrt{l}}, \gamma \frac{\alpha}{\sqrt{l}}) \\$$

其中 $\alpha \sim [0, 1]$ 是一个超参数，$l$ 表示网络层深度。

根据均匀分布的性质，使用 DS-Init 初始化后模型参数的方差会从 $\frac{\gamma^2}{3}$ 降到 $\frac{\gamma^2 \alpha^2}{3l}$，也就是说，$l$ 越大其输出的方差会越小。

上面的图中虚线部分则展示了，使用 DS-Init 初始化方法后每层的误差梯度。从图中可以看出，该初始化方法是有效的。利用 DS-Init 初始化方法来解决梯度消失问题的另一大优势是，无需修改模型结构，只需要修改初始化方法即可，简单有效又方便。

2.2 Merged Attention Model

随着模型深度的增加，计算量会变得很大，训练和推理时间都会大大增加。为了解决这个问题，作者提出 Merged Attention Model，该模型是 AAN（Average Attention Network） 的一种简化：移除了出了线性变换之外所有的矩阵运算:

$$\mathrm{SAAN}(\mathbf{S}^{l-1}) = \left[ \mathbf{M}_a(\mathbf{S}^{l-1}\mathbf{W}_v)\right]\mathbf{W}_o$$

其中 $\mathbf{M}_a$ 表示 AAN 中的 mask 矩阵。然后通过如下方式将其与 cross-attention 相结合：

$$\mathrm{MATT}(\mathbf{S}^{l-1}) = \mathrm{SAAN}(\mathbf{S}^{l-1}) + \mathrm{ATT}(\mathbf{S}^{l-1}, \mathbf{H}^L) \\\\ \bar{\mathbf{S}}^l = \mathrm{LN}(\mathrm{RC}(\mathbf{S}^{l-1}, \mathrm{MATT}(\mathbf{S}^{l-1})))$$

其中 $\mathbf{W}_o$ 在 SAAN 和 MATT 中共享， $\mathbf{H}^L$ 为编码器的输出， $\mathrm{ATT}$ 是 cross-attention。具体的结构图如下：

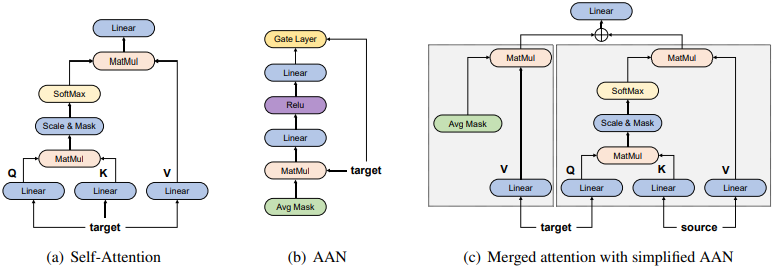
3. Pre-Norm for Deep Residual Network

除了对参数的方差进行归一化之外，Wang 等人首次指出 Transformer 中的层正则化位置对于训练一个深层网络至关重要。通过重新定位层正则化的位置将其置于每个子层的输入之前，便能够有效解决深层网络当中容易出现的梯度爆炸或者梯度消失现象，这对训练深层网络的影响在之前并未被研究过。

3.1 Pre-Norm

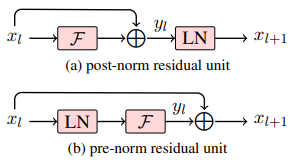
Transformer 的残差连接和 LayerNorm 组合方式称为 post-norm。具体的计算流程如图（a）所示：层输入->层计算->dropout->残差累加->层正则化。 这种方式可能出现的问题如第 1 节讨论，连乘形式的损失梯度很容造成梯度消失或者爆炸。因此，深层 Transformer 通常不容易收敛。

针对这个问题，作者提出 pre-norm 的组合方式，计算流程如图（b）所示：层输入->层正则化->层计算->dropout->残差累加。 我们来分析下这种组合方式的梯度形况。

$$x_{l+1} = x_l + \mathcal{F}(\mathrm{LN}(x_l); \theta_l)=x_l+\mathcal{F}(x_l;\theta_l)$$

我们仔细观察 pre-norm 会发现，它有一个重要的特性：

$$\begin{equation} \nonumber \begin{aligned} x_L &= x_{L-1} + \mathcal{F}(x_{L-1};\theta_{L-1}) \\\\ & = x_{L-2} + \mathcal{F}(x_{L-2};\theta_{L-2}) + \mathcal{F}(x_{L-1};\theta_{L-1})\\\\ & \cdots \\\\ &= x_l +\sum_{k=l}^{L-1} \mathcal{F}(x_k;\theta_k) \end{aligned} \end{equation}$$

这样 $x_L$ 相对 $x_l$ 的导数可以写作：

$$\frac{\partial x_L}{\partial x_l} = 1+ \sum_{k=l}^{L-1}\frac{\partial \mathcal{F}(x_k;\theta_k)}{\partial x_l}$$

将该式带入误差的导数公式：

$$\frac{\partial \mathcal{E}}{\partial x_l} = \frac{\partial \mathcal{E}}{\partial x_L} \times \left( 1+ \sum_{k=l}^{L-1}\frac{\partial \mathcal{F}(\mathrm{LN}(x_k);\theta_k)}{\partial x_l}\right)$$

对比一下 post-norm 的误差梯度：

$$\frac{\partial \mathcal{E}}{\partial x_l} = \frac{\mathcal{E}}{\partial x_L} \times \prod_{k=l}^{L-1}\left[\frac{\partial \mathrm{LayerNorm(y_k)}}{\partial y_k}\left(1+\frac{\partial \mathcal{F}(x_k;\theta_k)}{\partial x_k}\right) \right]$$

我们会发现，等号右边第二项从连乘变成了连加。这样就解决了连乘可能带来的梯度消失或者爆炸问题。同时，通过 pre-norm 的方式网络在反向更新时，底层网络参数可以直接获得顶层梯度的信息，而不经过其他的变换，使得误差信息更容易传递到底层。

3.2 Dynamic Linear Combination of Layers

对于深层网络来说，残差连接的方式可能准确度还不够，一个可能的原因是，只用了前一步的信息来预测当前的值。机器翻译的 “单步”特性导致模型可能会 “忘记”距离比较远的层。这就会导致底层的网络训练不充分，针对这个问题作者提出动态线性组合（Dynamic Linear Combination of Layers, DLCL）的方式在信息传递至下一层时对之前所有层的输出进行线性聚合。

令 $\{ y_0, …, y_l\}$ 表示 $0 \sim l$ 层的输出。定义 $l+1$ 层的输入：

$$x_{l+1} = \mathcal{G}(y_0, ..., y_l)$$

其中 $\mathcal{G}(\cdot)$ 是是一个整合之前各层输出的线性函数，定义如下：

$$\mathcal{G}(y_0,...,y_l) = \sum_{k=0}^l W_k^{(l+1)} \mathrm{LN}(y_k)$$

其中 $W_k^{(l+1)} \in \mathbb{R}$ 是一个可学习的标量，用来对每个输出层进行加权。

DLCL 可以看成一种普适的方法，如下图所示：

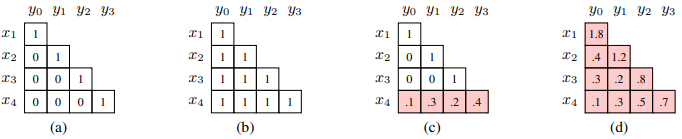
• （a）表示标准的残差网络：He et al. (2016)；
• （b）表示均匀权重的稠密残差网络：Britz et al. (2017)；
• （c）表示多层融合：Wang et al. (2018)；
• （d）表示表示本文的方法。

4. Experiments

• DS-Init 实验结果

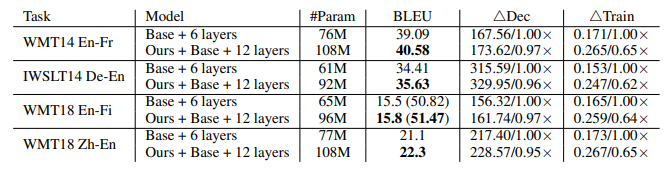
• Pre-norm 实验结果

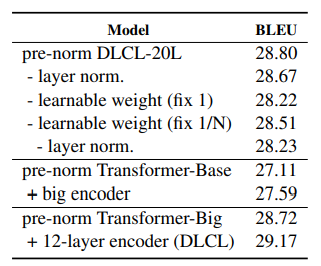
5. Personal Thought

本文介绍了两种加深 Transformer 的方法，一种是改变模型参数的初始化，一种是改变残差连接方式。无论哪一种目的都是解决深层 Transformer 的梯度消失/爆炸的问题。实际上还有几篇讨论加深 Transformer 的文章这里没有介绍，但是大致思路都差不多。

Kaiming 大神在2016年发表了一篇论文讨论 BN, activation 和 residual 之间的关系：Identity Mappings in Deep Residual Networks。结合关于加深 Transformer 的工作的各种方法来看，我们是不是可以大胆的猜测 Residual、LN、Initialization、Gradient 这四者之间，是否存在千丝万缕的联系？

Reference

1. Improving Deep Transformer with Depth-Scaled Initialization and Merged Attention. Biao Zhang, Ivan Titov, Rico Sennrich. 2019. ACL

2. Lipschitz Constrained Parameter Initialization for Deep Transformers. Hongfei Xu, Qiuhui Liu, Josef van Genabith, Deyi Xiong, Jingyi Zhang. 2020. arXiv: 1911.03179

3. Learning Deep Transformer Models for Machine Translation. Qiang Wang, Bei Li , Tong Xiao, Jingbo Zhu, Changliang Li, Derek F. Wong, Lidia S. Chao. 2019. arXiv: 1906.01787

4. On Layer Normalization in the Transformer Architecture Ruibin Xiong, Yunchang Yang, Di He, Kai Zheng, Shuxin Zheng, Huishuai Zhang, Yanyan Lan, Liwei Wang, Tie-Yan Liu. ICLR 2020 (reject)

5. 如何在NLP中有效利用Deep Transformer AI科技点评, 知乎

6. 香侬读 | Transformer中warm-up和LayerNorm的重要性探究 香侬科技，知乎