Transformer家族之Universal Transformer

Rogerspy

2020-05-11

NLP

字数统计: 2.6k字   |   阅读时长≈ 10分

自从 2017 年谷歌提出 Transformer 模型以后，其在多个任务上的表现都超过了前辈 RNN, 但是在某些任务上表现却差强人意，比如复制字符串（输入 abc， 输出 abcabc）。随后谷歌对原始的 Transformer 进行了改进，提出了 Universal Transformer 模型使其具有更强的泛用性，同时该模型也是图灵完备的。

1. Introduction

Transformer 解决了 RNN 的最大缺陷：无法并行处理输入序列以及最大长度依赖问题（梯度消失）。但是同时也放弃了 RNN 的两大优势：对迭代学习的归纳偏置（inductive bias towards learning iterative）和递归转换（recursive transformations），而这些优势在某些任务中起到了至关重要的作用。所以 Transformer 会在某些任务中被 RNN 轻易打败。

谷歌大脑的研究人员们针对这种情况，对 Transformer 进行了扩展，提出 Universal Transfomer 模型。该模型不仅保留了 Transformer 的并行能力和借助自注意力机制从距离较远的词中提取含义这两大优势，又引入时间并行的循环变换结构，相当于将 RNN 的两大优势也纳入其中。更重要的一点是：相比于 RNN 那种一个符号接着一个符号从左至右依次处理的序列处理方式，Universal Transformer 是一次同时处理所有的符号，而且 Universal Transformer 会根据自我注意力机制对每个符号的解释做数次并行的循环处理。

时间并行循环的大致计算过程如下：

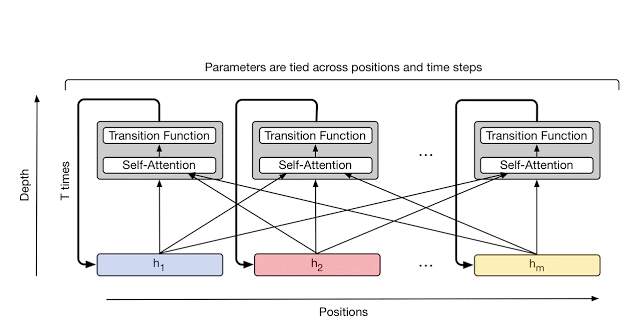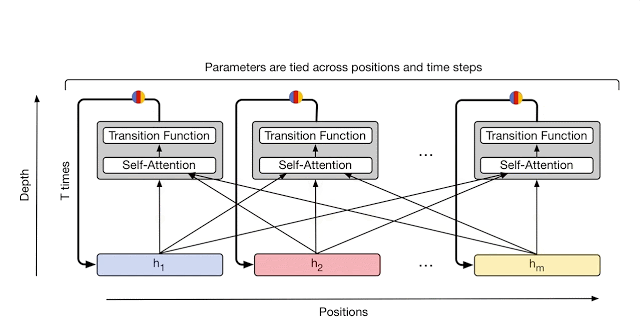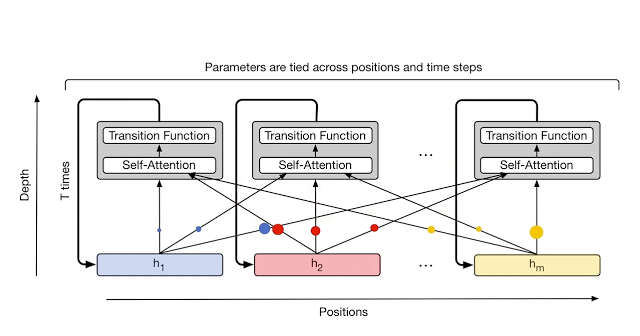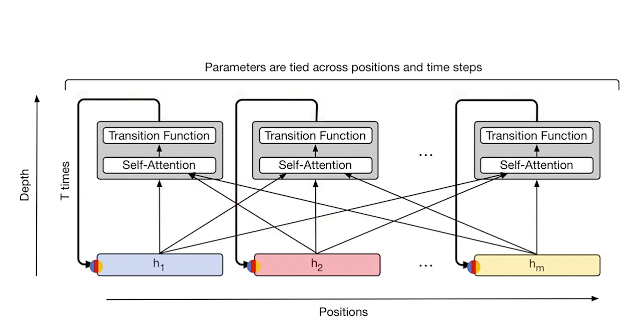
在每个步骤中，每一个符号（比如句子中的一个词）的信息都可以借助自注意力机制与所有其他的符号进行沟通，就和原本的 Transformer 一样。不过，要对每个符号应用几次这种变换（也就是循环步骤的数目）可以预先手工设置为某个值（比如设置为定制，或者设置与输入长度相关），也可以由 Universal Transformer 自己在执行中动态地选择。为了能够达到后一种效果，研究人员为每个位置加入了一个自适应计算机制，它可以自定义在每个词上计算的次数。

举个例子：I arrived at the bank after crossing the river

句子中 “I“, “river“ 等词意义比较明显，不存在什么歧义，所以模型可能只在这些词上计算 1 次（循环一次），但 “bank“ 就不一样了，这个词是一个歧c义词，需要通过上下文才能确定词义，因此，模型可能会多次计算该词的词义（循环多次）。这样的设定理论上讲，可以让 UT 具有更强的能力。

2. 模型结构

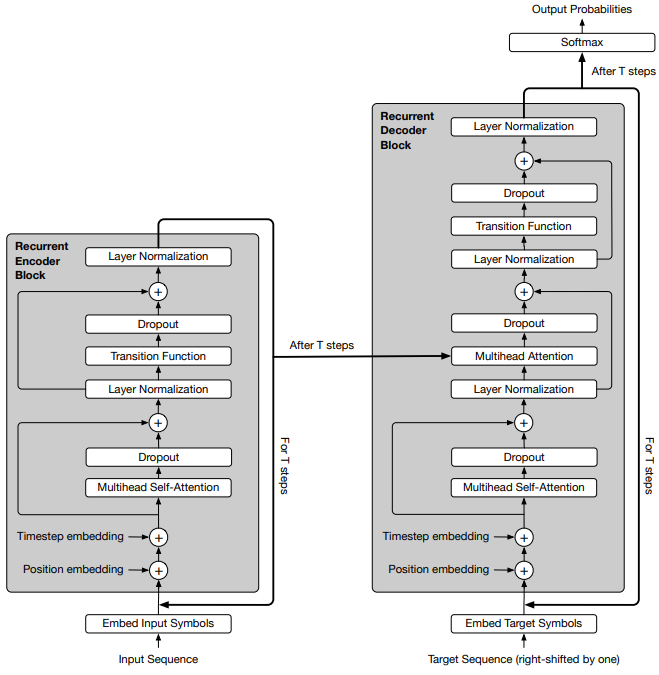
对比 Universal Transformer 结构图和 Transformer 结构图可以发现，两者主要有三个区别：

  • 循环结构
  • 位置编码多了一个 Timestep embedding;
  • FFN 变成了 Transition Function

在循环结构上，如上面讨论的，对于每个词的循环次数可以有两种方法确定：① 作为超参数人工设定，如同 Transformer 那样设成 6；② 模型自动设定，要实现这个功能，模型需要加入一个新的机制 —— 自适应计算时间 （Adaptive Computation Time，即 ACT）

下面我们针对这四个变化详细介绍一下。

2.1 Recurrent 机制

2.1.1 Encoder

给定输入序列长度 $m$，词向量维度 $d$，初始序列嵌入矩阵 $H^0 \in \mathbb{R}^{m \times d}$。$H^t$ 表示经过 $t$ 次循环以后的序列嵌入矩阵。

其中 $W^Q \in \mathbb{R}^{d \times d/k}$，$W^K \in \mathbb{R}^{d \times d/k}$， $W^V \in \mathbb{R}^{d \times d/k}$。

在第 $t$ 步时， $H^t \in \mathbb{R}^{m \times d}$ 的计算如下：

其中 $\mathrm{Transition}(\cdot)$ 为 Transition Function；$P^t$ 为 Timestep embedding （或者 coordinate embedding），在后面详细介绍。

2.1.2 Decoder

解码器与编码器的循环结构基本相同，只是多了一个接受编码器最终状态的另一个多头注意力，其输入的 $Q$ 来自解码器， $K$ 和 $V$ 来自编码器。

  • 训练

    训练的时候，对于一组输入输出序列样本解码器接受右移动一位的输出序列样本作为输入，相应解码器的自注意力机制也被修改成只能访问它左边的预测结果。每轮生成一个字符，通过 softmax 获得每个字符的输出概率：

    其中 $O \in \mathbb{R}^{d \times V}$。这部分和 Transformer 是一致的，不再赘述。

  • 推理

    在生成时编码器只运行一次而解码器反复运行。解码器接受的输入为已经生成的结果，每次(一次可以有多轮)的输出为下一个位置的符号概率分布。我们选择出现概率最高符号作为修订后的符号。

2.1.3 parallel-in-time recurrent

假设给定一个序列： $(a, b, c, d)$。UT 先将该序列经过 embedding 表示成 $(h^0_a, h^0_b, h^0_c, h^0_d)$ 初始化序列矩阵，然后经过 MultiHeadAttention 层和 Transition 层表示成 $(h^1_a, h^1_b, h^1_c, h^1_d)$。以此类推，经过 $t$ 次循环以后序列被表示成 $(h^t_a, h^t_b, h^t_c, h^t_d)$。

这个循环过程与 RNN 有着截然不同的计算方式。RNN 的循环计算过程是，先计算 $h^0_a$，然后依次计算$h^0_b, h^0_c, h^0_d$，然后进入下一个循环，直到 $t$ 步以后生成 $(h^t_a, h^t_b, h^t_c, h^t_d)$。也就是相当于对于 RNN 来讲，要循环计算 $t$ 次 $m$ 长度的序列，模型需要计算 $m \times t$ 次运算，而 UT 只需要计算 $t$ 次。

2.2 Coordinate Embedding

Transformer 中计算位置向量只需要考虑词的位置就好，这里又考虑了时间维度。

其中 $P^t \in \mathbb{R}^{m \times d}$，维度与序列矩阵保持一致。

2.3 Transition Function

根据任务的不同，作者使用两种不同的 transition function：可分离卷积或全连接神经网络。

2.4 Adaptive Computation Time (ACT)

所谓自适应计算时间，是 Graves 等人 2016 年 提出的一种算法，该算法能自动学习 RNN 需要计算多少轮。用在 UT 中，使得模型能够对序列中不同的词有不同的循环次数，比如序列 $(a,b,c,d)$ 中 $a$ 只循环计算 1 次， $b$ 可能计算 2次，$c$ 会计算 5 次， $d$ 计算 8 次。而每个词的循环计算次数由 ACT 决定。当某个位置“停止”后，它的隐状态直接拷贝到下一步，直到所有位置都停止循环。

简单来说 ACT 会计算每个位置上的词需要停止的概率 （$p \sim [0, 1]$），当 $p$ 大于某个阈值的时候该位置上的词及计算就会停止。为了避免死循环，还可以设置一个最大循环次数，当循环次数达到该值的时候，循环也会被强行停止。

3. Experiments

作者利用 bAbI 数据集和 WMT14 En-De 数据集在问答，语言模型，机器翻译等任务上做了充分的实验，实验结果表明 UT 的表现能达到更好的效果。上图我们只展示机器翻译的结果，更详细的实验可参看原文。

4. Personal Thought

关于 Universal Transformer 的模型部分我们就介绍完了，总的来说 UT 具备了一些 Transformer 不具备的能力，解决了一些原有的缺陷。在问答、语言模型、翻译等任务上的表现都有所提升。

  • Weight sharing：归纳偏置是关于目标函数的假设，CNN 和 RNN 分别假设 spatial translation invariance 和 time translation invariance，体现为 CNN 卷积核在空间上的权重共享和 RNN 单元在时间上的权重共享，所以 Universal Transformer 也增加了这种假设，使 recurrent 机制中的权重共享，在增加了模型表达力的同时更加接近 RNN 的 inductive bias。
  • Conditional Computation Time：通过加入 ACT 控制模型的计算次数，比固定 depth 的 Universal Transformer 取得了更好的结果。

但是还是有一些问题文章中并没有说的很清楚，可能为接下来进一步的研究和优化留出了空间：

  • 空间位置和时间位置向量的直接相加略显粗糙;
  • 为什么需要不同的 Transition Function，它们分别起到什么作用？
  • 图灵完备对模型有什么用？

5. UT with Dynamic Halting

作者在附录中给出了 Tensorflow 实现的 ACT 代码，这里抄录一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
# while-loop stops when this predicate is False
# i.e. all ((probability < threshold) & (counter < max_steps)) are False
def should_continue(u0, u1, halting_probability, y2, n_updates, u3):
    return tf.reduce_any(
        tf.logical_and(
            tf.less(halting_probability, threshold),
            tf.less(n_updates, max_steps)
        )
    )

# do while loop iterations until predicate above is False
(_, _, _, remainder, n_updates, new_state) = tf.while_loop(
    should_continue, ut_with_dynamic_halting, 
    (state, step, halting_probability, remainders, n_updates, previous_state)
)

# the computations in each step
def ut_with_dynamic_halting(
    state,
    step,
    halting_probability,
    remainders,
    n_updates,
    previous_state
):
    # Claculate the probablities based on the state
    p = common_layers.dense(state, 1, activation=tf.nn.sigmoid, use_bias=True)
    # Mask for inputs which have not halted yet
    still = tf.cast(tf.less(halting_probability, 1.0), tf.float32)
    # Mask for inputs which halted at this step
    new_halted = tf.cast(
        tf.greater(
            halting_probability + p * still_running, threshlod
        ), tf.float32
    ) * still_running
    # Mask of inputs which haven't halted, and didn't halt this step
    still_running = tf.cast(
        tf.less_equal(
            halting_probablity + p * still_running,
            threshold
        ), tf.float32
    ) * still_running
    # Add the halting prinbability for this step to the halting
    # pribabilities for those inputs which have not halted yet
    halting_probability += p * still_running
    # Compute remainders for the inputs which halteed at this step
    remaindes += new_halted * (1 - halting_probability)
    # Add the remainders to those inputs which halted at this step
    halting_probability += new_halted * remainders
    # Increment n_updates for all inputs which are still running
    n_updates += still_runnign + new_halted
    # Compute the weight to be applied to the new state and output
    #    0 when the input has already halted
    #    p when the input hasn't halted yet
    #    the remainders when it halted this step
    update_weights = tf.expand_dims(
        p * still_running + new_halted * remainders,
        -1
    )
    # Apply transformation to the state
    transformed_state = transition_function(self_attention(state))
    # Interpolate transformed and prevous states for non-halted inputs
    new_state = (
        transformed_state * update_weights\
        + previous_state * (1 - update_weights)
    )
    step += 1
    return (transformed_state, 
            step, 
            halting_probability, 
            remainders, 
            n_updates, 
            new_state)

Reference

  1. Universal Transformers, Mostafa Dehghani, Stephan Gouws, Oriol Vinyals, Jakob Uszkoreit Łukasz Kaiser, 2018, ICLR 2019
  2. Moving Beyond Translation with the Universal Transformer, Google AI Blog
  3. (简介)Universal Transformers, wywzxxz, 知乎
  4. 【NLP】Universal Transformers详解，李如，知乎
  5. Adaptive Computation Time for Recurrent Neural Networks, Alex Graves, 2016, arXiv: 1603.08983
 上一页

Transformer Gaussian

 评论