
接下来我们介绍一下Sharing Attention Weights for Fast Transformer这篇文章。实际上这篇文章之前还有两个关于加速Transformer推理的文章,一个类似Latent Transformer的引入离散隐变量的类VAE的方法,另一个是引入语法结构达到non-auto regression的方法。个人感觉没什么意思,就直接跳过了。本文要介绍的这篇文章比较有意思,引入共享权重的概念。从近期关于Bert小型化的研究(比如DistilBERT,ALBERT,TinyBERT等)来看,实际上Transformer中存在着大量的冗余信息,共享权重的方法应该算是剔除冗余信息的一种有效的手段,因此这篇文章还是比较有意思的。
1. Attention Weights
我们在介绍Transformer的时候说过,Multi-Head Attention其实和Multi-dimension Attention是一回事。在多维注意力机制中,我们希望每一维注意力都能学到不同的含义,但是实际上Lin et al. 2017研究发现,多维注意力机制经常会出现多个维度学到的东西是相同的的情况,即不同维度的注意力权重分布是相似的。
本文做了一个类似的研究,发现不同层之间的注意力权重也有可能具有相似的分布,说明不同层之间的注意力权重也在学习相同的信息。作者分别计算了不同层之间的注意力权重的JS散度,用以说明不同注意力权重有多大的差异性,下图是作者的计算结果:
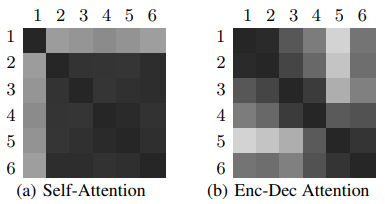
注意作者的意图是加速Transformer的推理速度,因此着重研究的是decoder部分,因此上图表示的decoder的JS散度矩阵。我们知道每个decoder block中包含两个注意力矩阵,一个是masked atteniton,一个是encoder-decoder attention,上图左图表示masked attnetion,右图表示encoder-decoder attention。图中颜色越深表示差异性越小,即两个注意力权重矩阵越相似。从图中可以看到self-attention部分的相似非常大,而encoder-decoder attention相似性虽然不如self-attention,但是1,2,3,4之间和5,6层之间的相似性也比较大。
由于不同层的注意力权重相似性较大,因此可以在不同层中共享同一个注意力权重,减少参数从而达到加速推理的目的。
这里作者只讨论了decoder的情况,还记得我们之前介绍过一篇论文An Analysis of Encoder Representations in Transformer-Based Machine Translation,讲的是在encoder的每一层注意力都学到了什么信息。这里我希望对比一下用本文的方法和上面的研究方法对比一下,看看得到结论是否能相互印证。因此我和本文的作者进行了交流,很遗憾的是作者并没有像decoder那样仔细研究encoder的情况,但是作者认为理论上encoder的情况应该是和decoder的self-attention的情况是一致的,因为encoder中的attention和decoder的self-attention层都是对单一的序列进行编码,不同的是前者是对源序列,后者是对目标序列,因此两者应该有相似的表现。虽然作者没有计算encoder注意力权重的JS散度,但是在实验过程中,尝试过对encoder的注意力进行共享,发现第1, 2层计算,3-6层使用第1层的权重,此种情况下对性能也未发现明显的下降趋势,因此作者认为encoder端不同层的注意力权重同样存在着较多的相似情况。
2. 模型结构
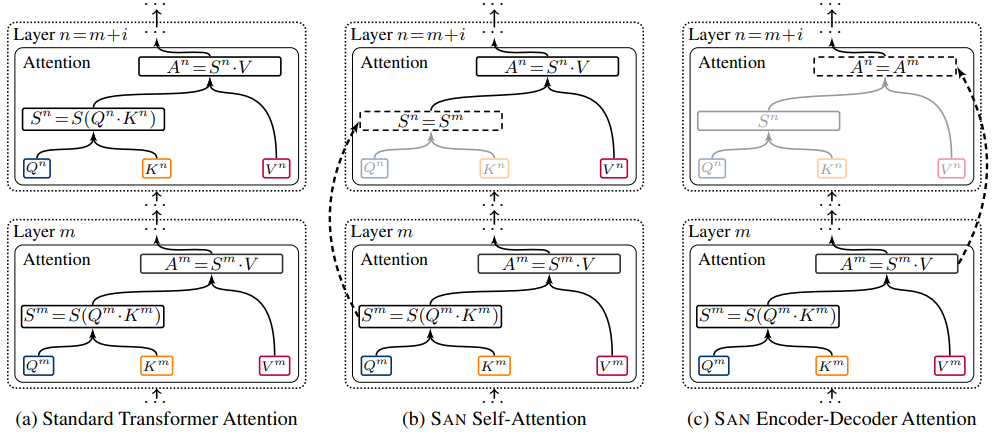
模型结构如上图。其实SAN的基本想法很简单,就是计算一次注意力权重,多次重复使用。具体的数学描述如下:
- Self-Attention
定义第$m$层的注意力自注意力权重矩阵为:
有了第$m$层的注意力权重,把它共享给第$m+1$层:
其中$\pi$表示有多少层共享第$m$层的注意力权重,比如对于一个6层的decoder来说,我们可以让前两层共享一个权重矩阵$\pi_1=2$,让后面的4层共享两一个权重矩阵$\pi_2=4$,具体的共享策略在后面介绍。
- Encoder-Decoder Attention
对于encoder-decoder注意力层来说,采取同样的操作。但是为了进一步加速推理,这里作者采用了一个小技巧,即$K, V$使用encoder的输出:
其中$A^m$是第$m$层的 注意力输出,$V$是encoder的输出。
另外为了减少内存消耗,共享的注意力权重只需要拷贝给相应的层即可,不需要配置到在每一层的内存中去。
3. Learning to Share
那么,现在的问题是,我们怎么知道那些层需要共享注意力权重呢?一个最简单的方法就是遍历测试,然后在development set上进行微调。显然这不是最优的方法,因为我们要在不同的程度上控制注意力权重的共享程度。
这里作者提出采用动态策略——利用JS散度计算层与层之间的相似度:
其中$\mu(i, j)$表示第$i$层和第$j$层的JS相似度,$\delta(i,j)$表示Kronecker delta function。上式表示$m,n$层之间的相似性,当$\mathrm{sim}(m,n) > \theta$时那么$m,n $层就共享注意力权重。
首先从第一层开始计算满足$\theta$阈值的最大的$\pi_n$,如此往复,直到所有的注意力层都计算完了。这个时候我们会得到一个注意力权重的共享策略$\{\pi_1, …, \pi_N\}$,$\pi_i$实际上前面已经解释了表示什么,但是为了更直观的解释,这里我们还是举个例子吧:
假设deocder有6层注意力层,共享策略为$\{\pi_1=2,\pi_2=4\}$,表示第$1,2$层共享注意力权重,第$3,4,5,6$共享注意力权重。
一旦共享策略确定了下来之后,我们要重新训练模型,对注意力权重进行微调,直到模型收敛。

4. 实验结果
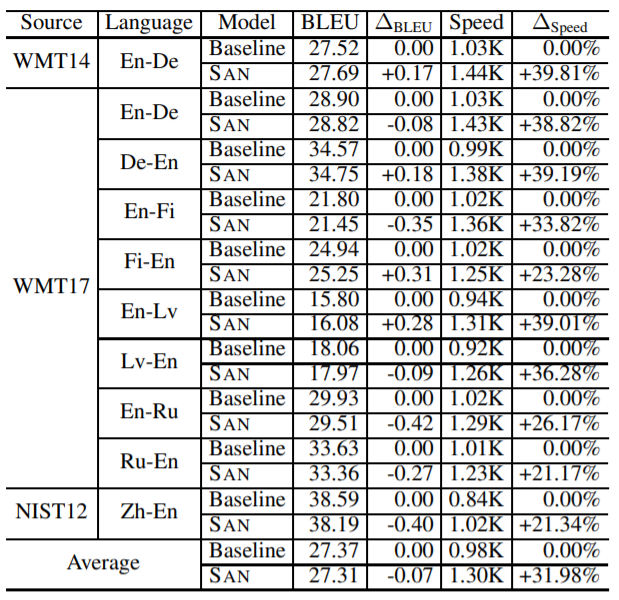
5. 参考资料
Sharing Attention Weights for Fast Transformer Tong Xiao et al., 2019



