Transformer家族之Latent Transformer

之前提到Auto-regression的decoding方法使得transformer在推理上的表现很慢，所以很多研究者在这方面做了很多研究，本文就介绍一个使用Non-Auto Regression的方法——Discrete Latent Variable。该方法与Auto-regression方法相比，效果上要稍差 一些，但是取得了比其他Non-auto regression方法都好的结果，而效率上也有很大的提升。

1. 简介

1.1 Auto-Regression

RNN在机器翻译领域有着非常重要的应用，但是它本身由于不能进行并行计算，限制了它的效率，所以后来有些研究者希望能用CNN替代RNN。而Transformer的横空出世，使得机器翻译在训练效果和效率上都上了一个台阶，但是仍然存在一个问题。

Transformer在生成一个序列的时候，通常需要根据之前的序列来预测下一个词，即当预测$y_n$时，需要利用$y_1, y_2, …, y_{n-1}$作为模型的输入。所以transformer在生成序列的时候是一个词一个词的生成，每生成一个词就需要进行一次推理，因此造成效率很低。这也就是所谓的Auto-regression问题。而transformer的auto-regression问题比RNN和CNN更加严重，因为RNN是根据前一个状态预测下一个状态，CNN是根据前K（kernel大小）个状态预测下一个状态，而transformer则是利用之前的所有状态预测下一个状态。虽然transformer在训练的时候可以很高效的训练，这是因为训练时的输出序列都已知，所以不需要auto-regression；但在进行decoding的时候输出是未知的，必须进行auto-regression，所以效率反而更低。

1.2 Latent Transformer

为了克服Auto-regression问题，Kaiser et al. 2018提出使用离散隐变量方法加速decoding推理。这种方法算不上真正解决了Auto-regression问题，但是算是对问题进行了优化吧，或者应该叫做Semi-auto regression。

这种方法简而言之就是，先用auto-regression生成一个固定长度的短的序列$l= \{l_1, l_2, …, l_m\}$，其中$m<n$，然后再用$l$并行生成$y = \{y_1, y_2, …, y_n\}$。为了实现这种方法，我们需要变分自编码器。由于句子序列是离散的序列，在使用离散隐变量的时候会遇到不可求导的问题，因此如何解决这个问题就需要一些离散化的技术了。

2. 离散化技术

我们主要介绍四种离散化技术：

• Gumbel-softmax (Jang et al., 2016; Maddison et al., 2016)
• Improved Semantic Hashing (Kaiser & Bengio, 2018)
• VQ-VAE (van den Oord et al., 2017)
• Decomposed Vector Quantization

给定目标序列$y=\{y_1, y_2, …, y_n\}$，将$y$输入到一个编码器（自编码器中的编码器，并非机器翻译模型中的编码器，下文的解码器同理，如非特殊说明encoder和decoder指的都是自编码器中的编码器和解码器）中产生一个隐变量表示$enc(y) \in \mathbb{R}^D$，其中$D$是隐变量空间的维度。令$K$为隐变量空间的大小，$[K]$表示集合$\{1, 2, …, K\}$。将连续隐变量$enc(y)$传入到一个discretization bottleneck中产生离散隐变量$z_d(y) \in [K]$，然后输入$z_q(y)$到解码器$dec$中。对于整数$i, m$我们使用$\tau_m(i)$代表用$m$ bits表示的二进制$i$，即用$\tau_m^{-1}$将$i$从二进制转换成 十进制。

下面我们主要介绍discretization bottleneck涉及到的离散化技术。

实际上离散化技术是一个在VAE、GAN、RL中都有很重要应用的技术，本文只简单介绍它在文本生成方向的应用，而涉及到技术细节以及数学原理等更加详细的内容，以后会专门讨论，这里只说怎么用不说为什么。

2.1 Gumbel-Softmax

将连续隐变量$enc(y)$变成离散隐变量的方法如下：

$$l = W enc(y) , W \in \mathbb{R}^{K\times D}$$ $$z_d(y) = \mathrm{arg} \max_{i\in[K]}~ l_i$$

• 评估和推理时

$$z_q(y) = e_j$$

其中$e \in \mathbb{R}^{K \times D}$，类似词向量的查询矩阵；$j=z_d(y)$。这一步相当于编码器生成一个短句子序列，然后这个短句子序列作为解码器的输入，通过查询词向量矩阵将句子中的词变成向量。

• 训练时

使用Gumbel-softmax采样生成$g_1, g_2, …, g_K$个独立同分布的Gumbel分布样本：

$$g_i \sim -\log(-\log(u))$$

其中$u \sim U(0,1)$表示均匀分布。然后用下式计算softmax得到$w \in \mathbb{R}^K$:

$$w_i = \frac{\exp((l_i+g_i)/\tau)}{\sum_i\exp((l_i+g_i)/\tau)}$$

得到$w$以后我们就可以简单地用：

$$z_q(y) = we$$

来获得$z_q(y)$。

注意Gumbel-softmax是可导的，也就是说我们可以直接通过后向传播对模型进行训练。

2.2 Improved Semantic Hashing

Improved Semantic Hashing主要来源于Salakhutdinov & Hinton, 2009提出的Semantic Hahsing算法。

$$\sigma'(x) = \max(0, \min(1, 1.2\sigma(x)-0.1))$$

这个公式称为饱和sigmoid函数（Kaiser & Sutskever, 2016; Kaiser & Bengio, 2016），

• 训练时

在$z_e(y) = enc(y)$中加入高斯噪声$\eta \sim \mathcal{N}(0,1)^D$，然后传入给饱和sigmoid函数

$$f_e(y) = \sigma'(z_e(y) + \eta)$$

使用下式将$f_e(y)$进行离散化：

解码器的输入用两个嵌入矩阵计算$e^1, e^2 \in \mathbb{R}^{K \times D}$：

$$z_q(y) = e^1_{h_{e(y)}}+e^2_{1-h_{e(y)}}$$

其中$h_{e}$是从$f_e$或者$g_e$中随机选择的。

• 推理时

令$f_e=g_e$

2.3 Vector Quantization

Vector Quantized - Variational Autoencoder (VQ-VAE)是van denOord et al., 2017提出的一种离散化方法。VQ-VAE的基本方法是使用最近邻查找矩阵$e \in \mathbb{R}^{K\times D}$将$enc(y)$进行数值量化。具体方法如下：

$$z_q = e_k, k=\mathrm{arg} \min_{j\in [K]} \|enc(y) -e_j \|_2$$

对应的离散化隐变量$z_d(y)$是$e$矩阵中与$enc(y)$距离$k$索引最近的值。损失函数定义如下：

$$L = l_r +\beta\|enc{y}-sg(z_q(y)) \|_2$$

其中$sg(\cdot)$定义如下：

$l_r$即为给定$z_q(y)$后模型的损失（比如交叉熵损失等）。

使用下面两个步骤获得exponential moving average (EMA)：

1. 每个$j \in [K]$都用$e_j$；
2. 统计编码器隐状态中使用$e_j$作为最近邻量化的个数$c_j$。

$c_j$的更新方法如下：

$$c_j \leftarrow \lambda c_j+(1-\lambda)\sum_l 1[z_q(y_l)=e_j]$$

然后对$e_j$进行更新：

$$e_j \leftarrow \lambda e_j +(1+\lambda)\sum_l \frac{1[z_q(y_l)=e_j]enc(y_l)}{c_j}$$

其中$1[\cdot]$是一个指示函数，$\lambda$是延迟参数，实验中设置为$0.999$。

2.4 Decomposed Vector Quantization

当离散隐变量空间很大的时候VQ-VAE会有一个问题——index collapse：由于“富人越富，穷人越穷”效应，只有少数的嵌入向量能得到训练。

具体来说就是如果一个嵌入向量$e_j$距离很多编码器的输出$enc(y_1), enc(y_2), …, enc(y_i)$都很近，那么它就能通过上面$c_j$和$e_j$的更新更加靠近，到最后只有少数几个嵌入向量被用到。因此，本文提出了一个VQ-VAE的变种——DVQ使$K$值很大的时候也能做到充分利用嵌入向量。

2.4.1 Sliced Vector Quantization

Sliced vector quantization顾名思义，就是将$enc(y)$切成$n_d$个小的切片：

$$enc^1(y)\odot enc^2(y)...\odot enc^{n_d}(y)$$

其中每一个$enc(y)$的维度为$D/N_d$，$\odot$表示拼接。

2.4.2 Projected Vector Quantization

另一个方法是，使用固定的随机初始化投影集合：

$$\{ \pi^i \in \mathbb{R}^{D\times D/n_d} | i \in [n_d]\}$$

将$enc(y)$投影到$R^{D/n_d}$的向量空间中去。

3. Latent Transformer

介绍了这么多离散化的技术，下面就需要将这些离散化的技术应用到模型中去。给定输入输出序列对：$(x, y) = (x_1, x_2, …, x_k, y_1, y_2, …, y_n)$，Latent Transformer包含下面三个部分：

• $ae(y, x)$函数用来对$y$进行编码成$l=l_1, l_2, …, l_m$；
• 使用Transformer （即$lp(x)$）对$l$进行预测
• $ad(l, x)$函数并行化产生$y$

损失函数分成两部分：

1. $l_r = compare(ad(ae(y,x), x), y)$;
2. $l = compare(ae(y, x), lp(x))$

$$L = l_r + l$$

3.1 $ae(y,x)$函数

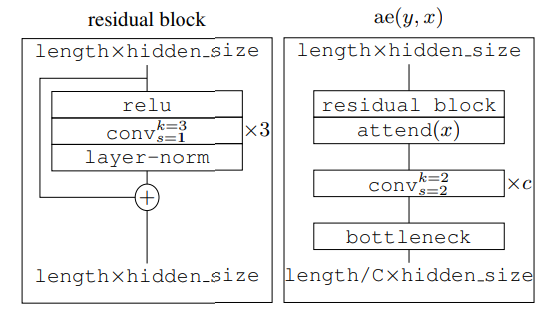
结构如图。其中bottleneck即为上面介绍的各种离散隐变量的方法。

3.2 $ad(y, x)$函数

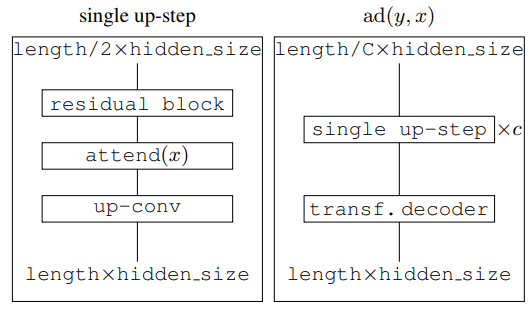
结构如图。

4. 实验结果

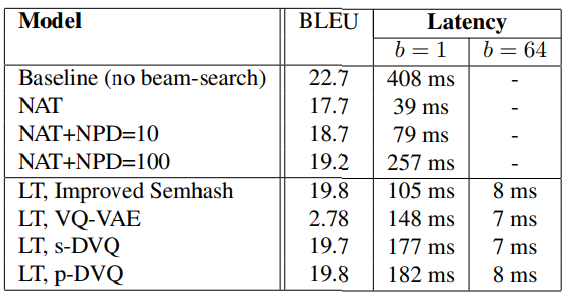
图中作为baseline的NAT是Gu et al. 2017另一种Non-auto regression的方法。

5. 参考资料

1. Fast Decoding in Sequence Models Using Discrete Latent Variables Kaiser et al., 2018

2. Categorical reparameterization with gumbel-softmax Jang et al. 2016

3. The concrete distribution: A continuous relaxation of discrete random variables Maddison et al., 2016

4. Can active memory replace attention? Kaiser, Łukasz and Bengio, Samy. 2016

5. Discrete autoencoders for sequence models Kaiser, Łukasz and Bengio, Samy. 2018
6. Neural GPUs learn algorithms Kaiser, Łukasz and Sutskever, Ilya. 2016
7. Non-autoregressive neural machine translation Gu et al., 2017
8. Neural discrete representation learning van den Oord et al., 2017
9. Semantic hashing Salakhutdinov, Ruslan and Hinton, Geoffrey E. 2009