预训练语言模型：Data noising smoothing

数据噪化（data noising）是一种非常有效的神经网络正则化的有段，通常被用在语音和视觉领域，但是在离散序列化数据（比如语言模型）上很少应用。本文尝试探讨给神经网络语言模型加噪声与 n-gram 语言模型中的平滑之间的联系，然后利用这种联系设计出一种噪声机制，帮助我们对语言进行建模。

1. 前言

给定一个序列：$X=(x_1, x_2, …, x_T)$，词表 $V$。我们可以对序列进行建模：

$$p(X)=\prod_{t=1}^T p(x_t|x_{<t})$$

传统的 n-gram 模型很难对 $t$ 很大的序列建模，因为随着 $t$ 的增加，$x_{<t}$ 的数量是以指数增加的。而神经网络可以处理更长的序列，因为神经网络处理的是隐状态而不是序列个数（参考之前的 RNN/CNN语言模型）。

以一个 $L$ 层的 LSTM 语言模型为例，第 $l$ 层的隐状态为 $h_t^{(l)}=f_\theta(h_{t-1}^{(l)}, h_t^{(t-1)})$。令 $h^{(0)}$ 为 $X$ 的 one-hot 编码，$t$ 时刻的模型输出为：

$$p_\theta(x_t|x_{<t}) = \text{softmax}(g_\theta(h_t^{(L)}))$$

其中 $g_\theta: \mathbb{R}^{|h|} \rightarrow \mathbb{R}^{|V|}$。然后通过优化交叉熵损失函数最大化似然估计 $p_\theta(X)$:

$$\mathcal{L}_\theta = - \sum_t \log p_\theta (x_t|x_{<t})$$

另外，我们还考虑另一个序列任务——seq2seq，输入序列 $X$ 输出序列 $Y$：

$$p(Y|X) = \prod_{t=1}^{T_Y} p(y_t|X, y_{<t})$$

损失函数：

$$\mathcal{L}_\theta = \sum_t \log p_\theta(y_t|X, y_{<t})$$

2. Smoothing & Noising

神经网络语言模型和 n-gram 语言模型一样，都是通过给定序列去预测下一个位置的元素，使用最大似然估计使模型参数达到最优。因此，两者其实有异曲同工之妙，但是神经网络容易过拟合，现有的正则化方法（比如 L2，dropout 等）都是从模型权重着手，并没有有效地分析和利用序列本身的特征。而 n-gram 模型则充分利用了序列本身的性质，因此分析 n-gram 的序列特征并将这些特征融入到神经网络中，对神经网络序列建模会有很大的帮助。

2.1 n-gram 中的平滑

之前介绍统计语言模型的时候，我们介绍过由于 n-gram 语言模型存在稀疏化问题，所以平滑技术至关重要。这里我们考虑插值平滑，比如 bi-gram：

$$p_{\text{inter}}(x_t|x_{t-1}) = \lambda \cdot p(x_t | x_{t-1}) + (1-\lambda) \cdot p(x_t)$$

其中 $0 \le \lambda \le 1$。

2.2 RNN 中的噪声

要想将 n-gram 中的平滑技术直接应用于 RNN 中会有一个问题，就是 RNN 中没有明确的计数。所以我们设计了两种加噪声的方法：

• unigram noising：对于 $x_i \in x_{<t}$，以 $\gamma$ 概率从样本中采样一个 unigram 来代替 $x_i$。

  原句：张三今年20岁。

  unigram noising：李四今年20岁。/ 老虎今年20岁。

• blank noising: 对于 $x_i \in x_{<t}$ ，以 $\gamma$ 概率将 $x_i$ 替换成 “_”。

  原句：张三今年20岁。

  blank noising：_今年20岁。

接下来我们就分析一下，这两种噪声与插值平滑之间的关系。

2.3 unigram noising as interpolation

我们先考虑最简单的情形——bigram。令 $c(x)$ 表示 $x$ 在原始数据中的个数，$c_\gamma(x)=\mathbb{E}_\tilde{x}[c(\tilde{x})]$ 表示在 unigram noising 情况下 $x$ 的期望个数，我们可得：

$$\begin{equation} \nonumber \begin{aligned} p_\gamma(x_t|x_{t-1}) &= \frac{c_\gamma(x_{t-1}, x_t)}{c_\gamma(x_{t-1})} \\\\ &= \frac{(1-\gamma)c(x_{t-1}, x_t) + \gamma p(x_{t-1}) c(x_t)}{c(x_{t-1})} \\\\ &= (1-\gamma) p(x_t|x_{t-1}) +\gamma p(x_t) \end{aligned} \end{equation}$$

其中 $c_\gamma(x) = c(x)$， 因为 $q(x)$ 是 unigram 分布。另外，最后一行是由于：

$$p(x_t) = \frac{c(x_t)}{n} \quad \& \quad p(x_{t-1}) = \frac{c(x_{t-1})}{n} \\\\ n = \frac{c(x_t)}{p(x_t)} = \frac{c(x_{t-1})}{p(x_{t-1})}$$

$n$ 表示训练集中总的 token。则最后一行的第二项为：

$$\begin{equation} \nonumber \begin{aligned} \frac{\gamma p(x_{t-1}) c(x_t)}{c(x_{t-1})} &= \gamma c(x_t) \cdot \frac{1}{n} \\\\ &= \gamma \frac{c(x_t)}{n} \\\\ &= \gamma p(x_t) \end{aligned} \end{equation}$$

我们可以看到 $p_\gamma(x_t|x_{t-1})$ 的加噪声形式与插值平滑数学形式上非常相似。我们还可以推导出更一般的形式，令 $\tilde{x_{<t}}$ 表示加噪声后的序列， 则：

$$\begin{equation} \nonumber \begin{aligned} p_\gamma(x_t|x_{<t}) &= \mathbb{E}_{\tilde{x_{<t}}}[p(x_t|\tilde{x}_{<t})] \\\\ &= \sum_J \underbrace{\pi(|J|)}_{p(|J| \text{swaps})} \sum_{x_K} \underbrace{p(x_t|x_J, x_K)}_{p(x_t|\text{noised context})} \prod_{z\in x_K} \underbrace{p(z)}_{p(\text{drawing z})} \end{aligned} \end{equation}$$

其中 $\pi(|J|)=(1-\gamma)^{|J|} \gamma^{t-1-|J|}$， 且 $\sum_J \pi(|J|)=1, J \in \{1,2,…,t-1\}$ 表示 token 没有发生变化的索引，$K$ 表示 token 被替换的索引。

2.4 blank noising as interpolation

Blank noising 可以也解释为 “word-dropout”（Kumar et al. 2015，Dai & Le 2015，Bowman et al. 2015）。令 $\tilde{x}_{<t}$ 表示别替换成 “_” 的序列，$x_J$ 表示没有替换的序列：

$$\begin{equation} \nonumber \begin{aligned} p_\gamma(x_t|x_{<t}) &= \mathbb{E}_{\tilde{x_{<t}}}[p(x_t|\tilde{x}_{<t})] \\\\ &= \sum_J \underbrace{\pi(|J|)}_{p(|J| \text{swaps})}\underbrace{p(x_t|x_J)}_{p(x_t|\text{noised context})} \end{aligned} \end{equation}$$

其中 $J \in \{1,2,…,t-1\}$，比如对于 3-gram:

$$p_\gamma(x_3|x_1, x_2) = \pi(2)p(x_3|x_1, x_2) + \pi(1)p(x_3|x_1, \_)+\pi(1)p(x_3|\_, x_2)+\pi(0)p(x_3|\_, \_)$$

其中 $\pi(i)=(1-\gamma)^i\gamma^{2-i}$。

3. 他山之石，可以攻玉

我们已经证明了噪化与平滑有异曲同工之妙，现在我们就可以从以下两个方面考虑如何提升噪声机制;

1. 自适应计算噪声概率 $\gamma$，用来反应特定输入子序列的置信度；
2. 利用更高阶的 n-gram 统计信息，选择一个比 unigram 更简单的分布 $q(x)$。

3.1 Noising Probability

假设有下面两个 bigram:

$$\text{“and the”} \quad \text{“Humpty Dumpty”}$$

第一个二元组在英语语料中非常常见，它的概率非常容易估计，因此不应该用低阶的分布进行插值。直观上来说，我们希望定义一个 $\gamma(x_{1:t})$ 对于常见的二元组尽可能少地被噪化。

第二个二元组就比较罕见了，但是这个二元组非常特殊，因为在英语语料中 “Humpty” 后面通常跟着的就是 “Dumpty”，同样的 “Dumpty” 前面的通常也是 “Humpty”，即这两个单词通常是成对出现的，这样的二元组我们称之为 “sticky pair”。构成 sticky pair 的词之间有很强的互信息，这样的二元组更类似于 unigram，我们希望可以避免二元组向一元组逼近。

令 $N_{1+}(x_1,\cdot)=|\{x_2:c(x_1, x_2)>0\}|$ 表示以 $x_1$ 为开头的二元组的种类，比如 $\{张三: 3, 张四: 4\}$ 其中以“张” 为前缀的二元组总数为 $3+4=7$，而以“张”为前缀的二元组的种类为 $2$（“张三”，“张四”）。根据对上面两个二元组的分析，我们可以设计噪声概率 $\gamma$：

$$\gamma_{AD}(x_1) = \gamma_0\frac{N_{1+}(x_1, \cdot)}{\sum_{x_2}c(x_1, x_2)}$$

其中 $0 \le \gamma_0 \le 1$，因此 $0 \le \gamma_{AD} \le 1$。如果我们忽略掉句子结束符的影响，则 $\sum_{x_2} c(x_1, x_2)=c(x_1)$。

• 当以 $x_1$ 为前缀的二元组总数固定，其不同组合的中类越少的时候，$x_1$ 被噪化的概率越小。对应上面第一个分析，当总数一定，但是组合种类越少，那么其中某一种的组合就越常见，$x_1$ 就越不应该被噪化。 $$\gamma_{AD}(\text{and}) = \gamma_0 \frac{N_+(\text{and}, \cdot)}{c(\text{and})} \quad$$ 假设 “and” 组成的二元组是平均分布的，则 $c(\text{and})= \mathbb{E}(c(\text{and, the})) \times \mathbb{E}(N_+(\text{and, the}))$ ，当 $\mathbb{E}(c(\text{and, the}))$ 越大的时候，$\mathbb{E}(N_+(\text{and, the}))$ 就会越小，则 $\gamma_{AD}(\text{and})$ 就越小。

3.2 Proposal distribution

假设有下面两个二元组：

$$\text{“San Francisco”} \quad \text{“New York”}$$

这两个二元组在语料中都非常常见，所以 “Francisco” 和 “York” 也非常常见。但是 “Francisco” 和 “York” 通常是跟在 “San” 和 “New” 后面，所以当使用 unigram 频率时它们也不应该有很高的噪声概率。相反，最好增加具有不同历史的一元组的提议概率，或者更准确地说是完成大量二元组类型的一元组。因此，我们令：

$$q(x) \propto N_{1+}(\cdot, x)$$

• 当以 $x$ 为结尾的二元组种类越少，被采样到的概率就会越低。假设语料中 “New York” 有 1 万条，但是 “York” 只与 “New” 组成二元组，即 $N_+(\cdot, \text{York})=1$，则 $q(x) \sim 1/10000$。

注意这个时候，我们除了会对 $x_{1:t-1}$ 进行噪化，同样也会对预测值 $x_t$ 进行噪化。结合 $q(x)$ 和 $\gamma_{AD}(x_1)$ 我们就可以得到 Kneser-Ney 平滑的噪化模拟了。

1. 我们以 $\gamma_{AD}(x)$ 的概率决定 $x$ 是否会被噪化（替换成 “_” 或者其他 token）;

2. 然后如果我们选择 ngram noising 的话，以 $q(x)$ 的概率对替他 token 进行采样，用来替换被 $\gamma_{AD}(x)$ 选中的 token。

下表总结了不同的噪化机制：

4. Experiments

4.1 Language Model

• Penn Treebank

  

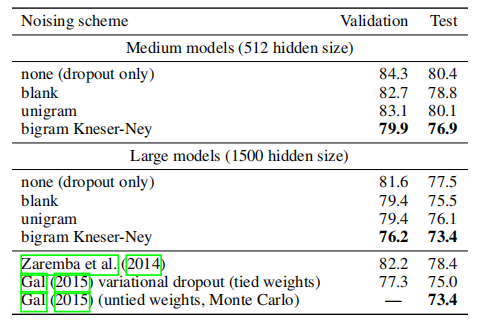
• Text8

  

4.2 Machine Translation

• IWSLT 2015（English-German）

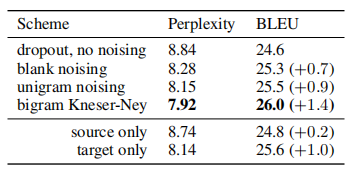
Reference

1. Data Noising as Smoothing in Neural Network Language Models, Ziang Xie, Sida I. Wang, Jiwei Li, Daniel Lévy, Aiming Nie, Dan Jurafsky, Andrew Y. Ng. ICLR, 2017
2. Ask me anything: Dynamic memory networks for natural language processing, Ankit Kumar, Ozan Irsoy, Jonathan Su, James Bradbury, Robert English, Brian Pierce, Peter Ondruska, Ishaan Gulrajani, and Richard Socher. arXiv preprint arXiv:1506.07285, 2015.
3. Generating sentences from a continuous space., Samuel R Bowman, Luke Vilnis, Oriol Vinyals, Andrew M Dai, Rafal Jozefowicz, and Samy Bengio. arXiv preprint arXiv:1511.06349, 2015.
4. Semi-supervised sequence learning.https://arxiv.org/pdf/1511.01432.pdf Andrew M Dai and Quoc V Le. In Advances in Neural Information Processing Systems, pp. 3061–3069, 2015.