数据结构与算法：优先队列（priority queue）

Rogerspy

2021-09-05

数据结构与算法

字数统计: 949字 | 阅读时长≈ 4分

本文介绍优先队列，并用 Python 实现。

1. 简介

优先队列是一种特殊的队列类型，队列中每个元素都包含一个优先级值。每个元素根据优先级的大小进行处理，即优先级越高，对应的元素越早处理。

但是，如果两个元素的优先级一样的话，根据他们在队列中的先后进行处理。

1.1 分配优先级

通常情况下，元素值本身就是优先级。比如，元素值越高则优先级越高，或者元素值越低优先级越高。当然，我们也可以根据具体需要来设置优先级。

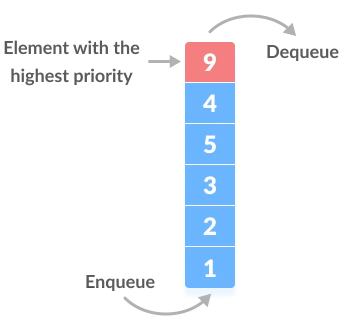
1.2 优先队列与常规队列的区别

在常规队列中，遵守先进先出规则；而在优先队列中，根据优先级删除值，首先删除优先级最高的元素。

1.3 优先队列的实现方式

优先队列的实现有多种方式，比如数组、链表、堆以及二叉树等。其中堆更加高效，所以下面我们以堆实现的优先队列为例进行介绍。因此，在此之前需要先了解堆数据结构：max-heap and mean-heap。

不同实现方式的复杂度对比：

Operations	peek	insert	delete
Linked List	`O(1)`	`O(n)`	`O(1)`
Binary Heap	`O(1)`	`O(log n)`	`O(log n)`
Binary Search Tree	`O(1)`	`O(log n)`	`O(log n)`

2. 优先队列的基本操作

优先队列的基本操作包括：插入、删除、查询。

2.1 插入

通过下面的步骤向优先队列中插入元素（max-heap）:

在树的末尾插入元素

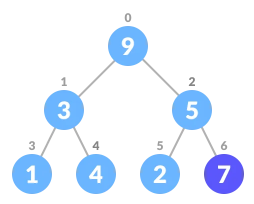
将树进行堆化

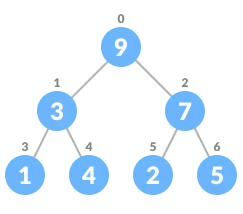
在优先队列中（max-heap）插入元素的算法如下：

If there is no node, 
  create a newNode.
else (a node is already present)
  insert the newNode at the end (last node from left to right.)
  
heapify the array

对于 Min heap，上面的算法中 parentNode 永远小于 newNode。

2.2 删除

通过下面的步骤从优先队列中删除元素（max heap）：

选择要删除的元素
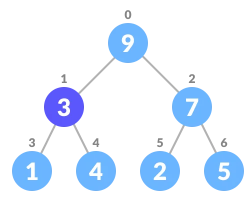
与最后一个元素位置进行交换
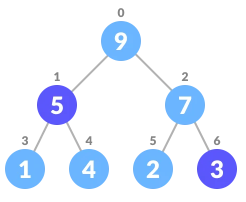
删除最后一个元素
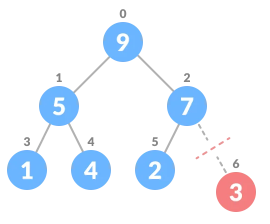
将树进行堆化

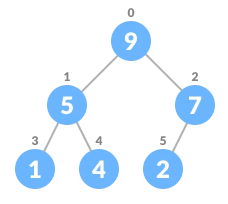
从优先队列中删除元素的算法：

If nodeToBeDeleted is the leafNode
  remove the node
Else swap nodeToBeDeleted with the lastLeafNode
  remove noteToBeDeleted
   
heapify the array

对于 Min Heap，上面算法中的 childNodes 一直 currentNode。

2.3 查询

对于 Max heap，返回最大元素；对于 Min heap，返回最小值。

对于 Max heap 和 Min heap 来说，都是返回根节点：

1	return rootNode

2.4 选取最大值最小值

抽取最大值返回从最大堆中删除后具有最大值的节点，而抽取最小值则返回从最小堆中删除后具有最小值的节点。

3. Python 实现优先队列

# Priority Queue implementation in Python


# Function to heapify the tree
def heapify(arr, n, i):
    # Find the largest among root, left child and right child
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    # Swap and continue heapifying if root is not largest
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)


# Function to insert an element into the tree
def insert(array, newNum):
    size = len(array)
    if size == 0:
        array.append(newNum)
    else:
        array.append(newNum)
        for i in range((size // 2) - 1, -1, -1):
            heapify(array, size, i)


# Function to delete an element from the tree
def deleteNode(array, num):
    size = len(array)
    i = 0
    for i in range(0, size):
        if num == array[i]:
            break

    array[i], array[size - 1] = array[size - 1], array[i]

    array.remove(size - 1)

    for i in range((len(array) // 2) - 1, -1, -1):
        heapify(array, len(array), i)


arr = []

insert(arr, 3)
insert(arr, 4)
insert(arr, 9)
insert(arr, 5)
insert(arr, 2)

print ("Max-Heap array: " + str(arr))

deleteNode(arr, 4)
print("After deleting an element: " + str(arr))