ROC-AUC原理及计算方法

本文转载自知乎用户码农要术的文章 衡量指标篇：ROC-AUC。

1. 历史起源

1941年，日军偷袭珍珠港，太平洋战争由此爆发。美军的雷达操作员（Radar operator）开始忙碌了起来，他们要识别出雷达屏幕上的光点是不是日本的战机。

因为光点也有可能是我方军舰，也有可能是噪声。为了衡量识别的性能，研究者们设计了ROC曲线（Receiver operating characteristic curve）。所谓 Receiver 就是雷达接收器，operating characteristic 则是表明雷达操作员（Radar operator）的识别能力。

后来，ROC曲线被应用到了医学领域，还有机器学习领域。虽然名字比较奇怪，但是从诞生之初，ROC 曲线的目的就是衡量分类的性能。AUC 是 ROC 曲线下的面积（ Area Under the ROC Curve），有一些优雅的性质，我们后面再说。

想讲清楚 ROC曲线，先要讲一下混淆矩阵。

2. 混淆矩阵

先从两类开始说起，Positive 和 Negative，医学上叫阳性和阴性，机器学习称之为正例和负例。经过分类器的决策后，一般情况下，正例预测的有对有错，负例预测的也有对有错。这样数据会被划分成4部分：正例预测对（True Positive），正例预测错（False Negtative），负例预测对（True Negative），负例预测错（False Positive）。

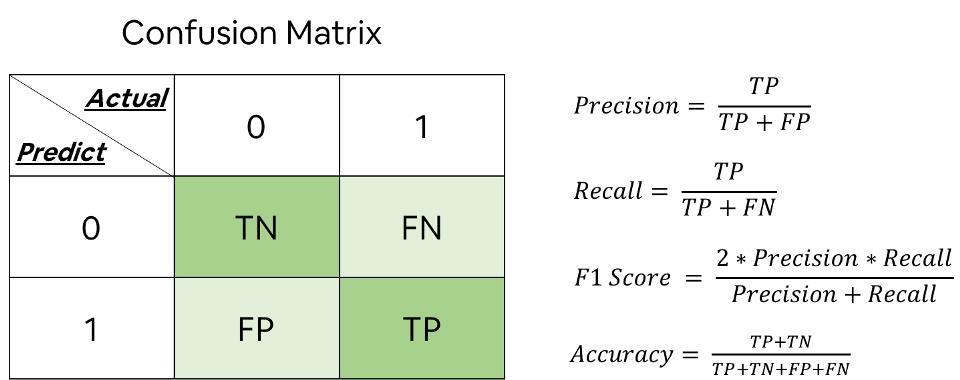
3. 如何衡量分类器的好坏？

如何衡量一个分类器是有效的，而不是随机结果？还是以雷达识别敌舰这个场景来说明。

3.1 两个假设

• 正负例等比例分布

• 分类器输出是离散值, 也就是 label 的集合

此时预测为正的结果可以划分成两部分：$TP$ 和 $FP$。比较两者关系，有如下结论：

1. 如果分类器是随机抽样，那么模型的输出和正负例比例一致。也就是 $TP=FP$。这个时候向识别出来的敌舰(预测为正的样本)开炮就是无差别攻击。
2. 如果 $TP>FP$, 可以说分类器有一定的甄别能力，战争中可以做到伤敌一千，自损八百。
3. 如果是 $TP<FP$ ,则说明分类器太差了，都不如随机抽样。用在战争中可以做到伤敌八百，自损一千。

3.2 一个假设

分类器输出是离散值, 也就是 label 的集合

这个时候在用TP和FP的绝对值做对比就显得不公平, 举个例子，我方军舰10艘，敌方军舰100艘。预测并且击沉我方军舰 8 艘，敌方军舰 9 艘.绝对数量上确实是占优势，但是我方基本全军覆没，敌方绝大多数战力仍然保留。样本不均衡时，就得做归一化，看相对值。

这里引入两个概念：$TPR$ （True Positive Rate），$FPR$（False Positive Rate）

$$TPR = \frac{TP}{TP+FN} \\\\ FPR = \frac{\mathrm{FP}}{FP+TN}$$

$TPR$ 就是正例中预测正确的比率。$FPR$ 就是负例预测错的比例。

$TPR$ 和 $FPR$，比较两者关系，有如下结论：

1. 如果分类器是随机抽样，那么模型的输出和正负例比例一致。也就是 $TPR=FPR$。这个时候向识别出来的敌舰(预测为正的样本)开炮就是无差别攻击。
2. 如果 $TPR>FPR$, 可以说分类器有一定的甄别能力，战争中伤敌的比率高于自损的比率。
3. 如果是 $TPR<FPR$ ,则说明分类器太差，不如随机抽样。战争中伤敌的比率低于自损的比率。

把 $TPR$ 和 $FPR$ 可视化，在 “分类器输出是离散值, 也就是 label“ 的假设下，$TPR$ 和 $FPR$ 是确定的，在二维坐标系上就是一个点。这个点就是 ROC 曲线的雏形。如下图：

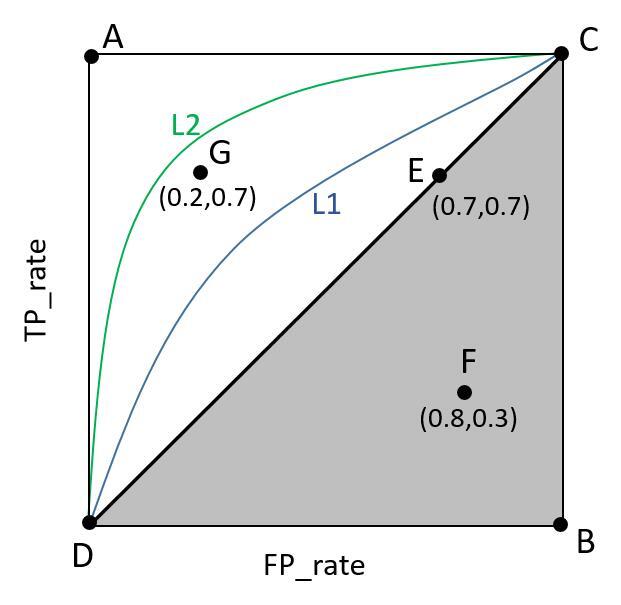
图中，E 点就是随机抽样 （$TPR=FPR$）。A，B，D点表示分类器有一定的甄别能力（$TPR>FPR$）。其中 A 点对应的是一个完美的分类器，所有的正例被识别正确（$TPR=1$），所有的负例没有识别错误（$FPR=0$）。F 点就是分类器太差（$TPR<FPR$），不如随机抽样。

3.3 另一个假设

分类器输出连续值

此时需要确定一个阈值来决定混淆矩阵和 $TPR$，$FPR$。

$TPR$ 的计算如下图所示：

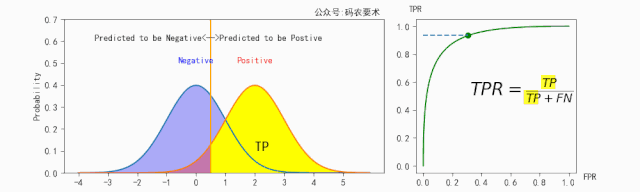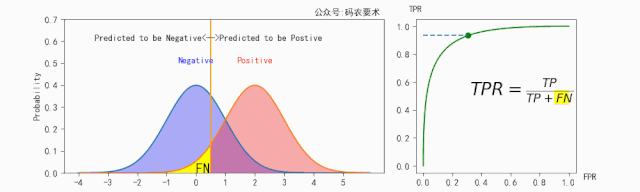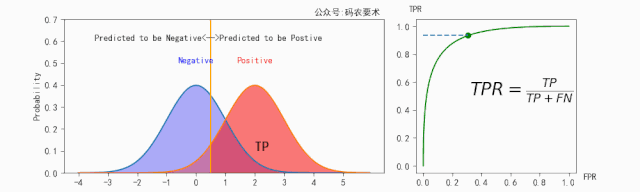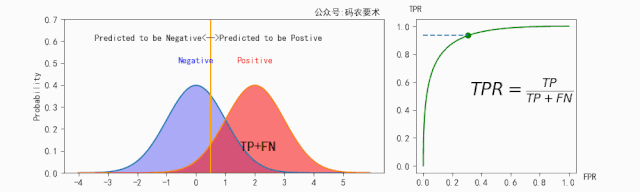
$FPR$ 的计算如下图所示：

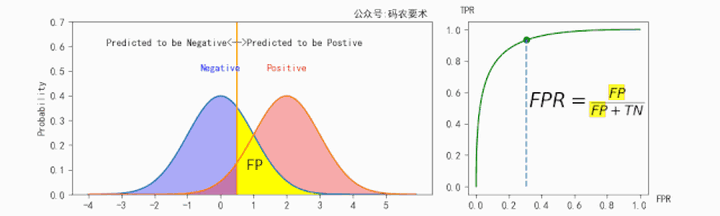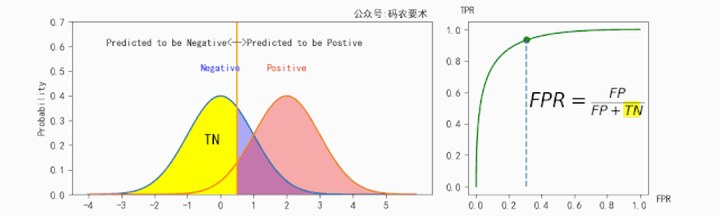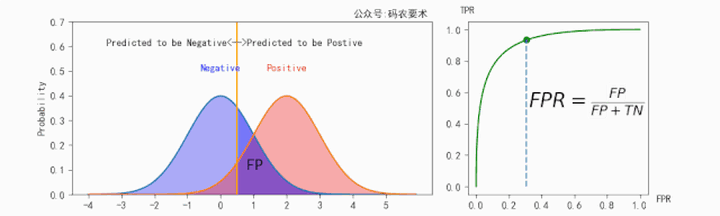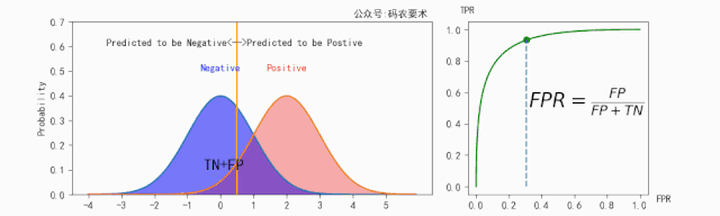
对于同一个分类器，不同的阈值对应不同的 $TPR$ 和 $FPR$，遍历阈值，即可得到 ROC 曲线。如下图：

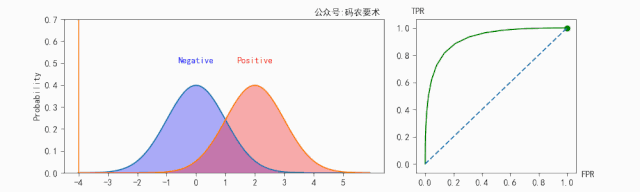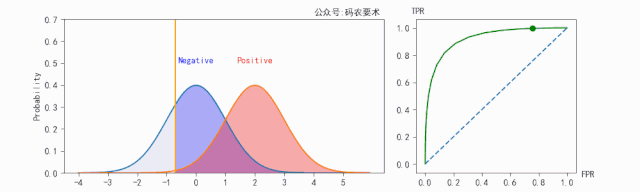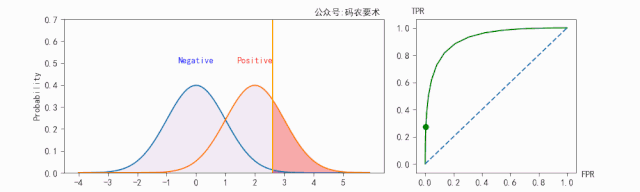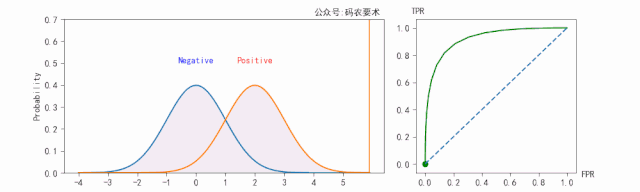
对于一个分类器，固定阈值，则得到一条 ROC 曲线。不同分类器会使预测的数据分布不同，在固定阈值的情况下，ROC 曲线变化如下图：

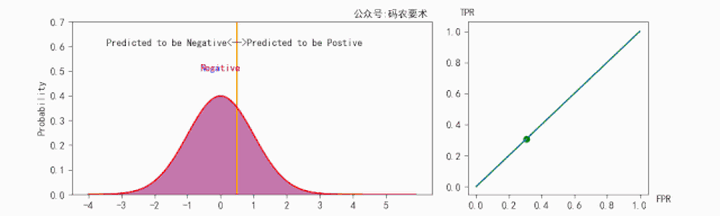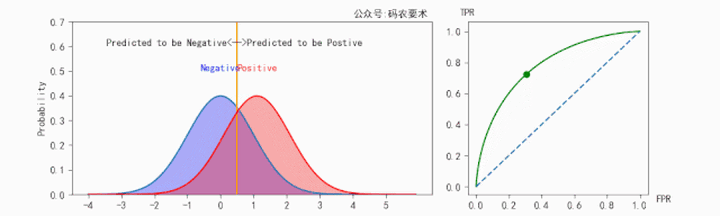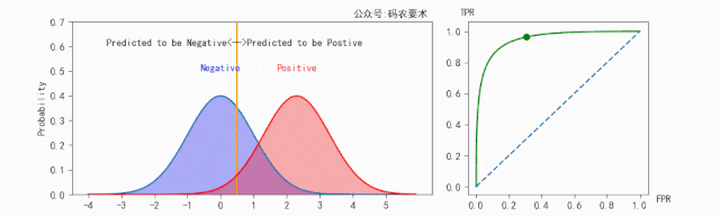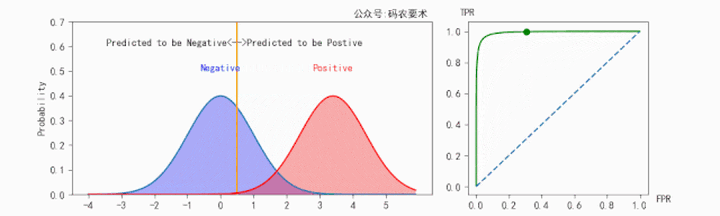
直观来看，分类器的区分度越好，ROC 曲线则越往左上角靠拢。AUC 就越大。怎么解释？

4. AUC 的概率解释

如果把 ROC 曲线看成是 $TPR$ 对 $FPR$ 的函数，$TPR=F(x)$ 我们对这个函数进行积分。如下图所示：

$$AUC = \int_{0}^1F(x)dx$$

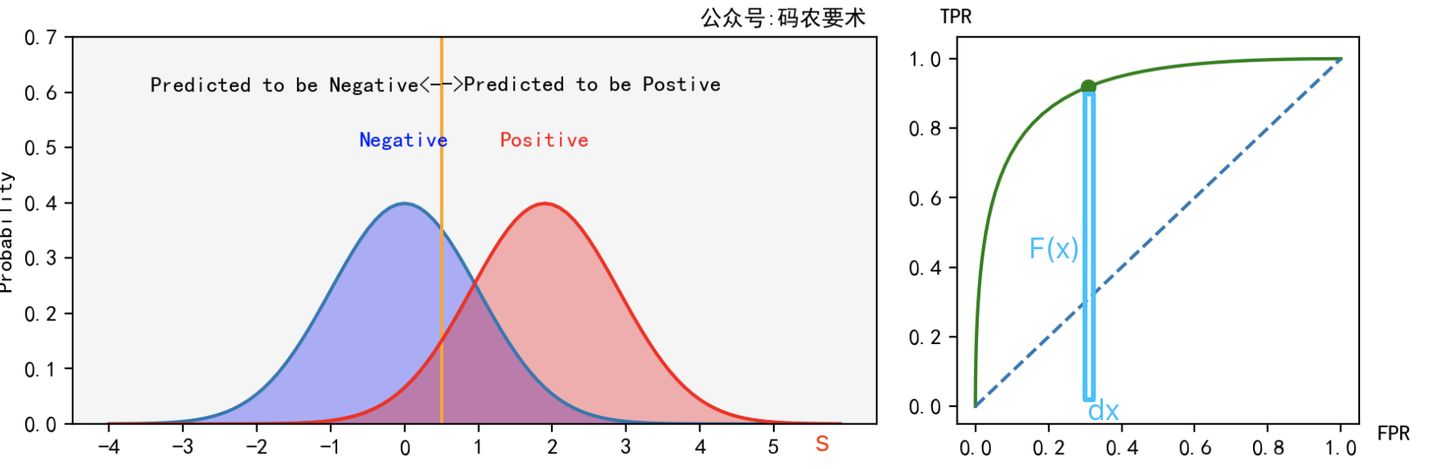
假设样本标签为 $y$，模型预测得分为 $s$，阈值为 $t$，正例的概率密度函数为 $f_1(s)$，负例的概率密度函数为 $f_0(s)$，则有

$$TPR = F(x) = \int_t^\infty f_1(s)ds = P(s>t|y=1) \\\\ FPR = x = \int_t^\infty f_0(s)ds = 1-\int_{-\infty}^t f_0(s)ds$$

$x$ 是 $t$ 的积分上限函数，根据积分上限函数的性质，得到

$$\frac{dx}{dt} = \frac{d}{dt}(1-\int_{-\infty}^t f_0(s)ds) = -f_0(t) \\\\ dx = -f_0(t)dt = -P(s'=t|y'=0)dt$$

则有

$$\begin{equation} \nonumber \begin{aligned} AUC &= \int_0^1F(x)dx \\\\ &= \int_{\infty}^{-\infty} F(x)(-f_0(t))dt \\\\ &= \int_{-\infty}^{\infty} F(x)f_0(t)dt \\\\ &= \int_{-\infty}^{\infty} P(s>t|y=1)f_0(t)dt \\\\ &= \int_{-\infty}^{\infty} P(s>t|y=1)\times P(s/=t|y'=0)dt \\\\ &= \int_{-\infty}^{\infty} P(s>s'\ \&\ s'=t|y=1\ \&\ y'=0)dt \\\\ &= P(s>s'|y=1\ \&\ y'=1) \end{aligned} \end{equation}$$

上面推导需要解释一下：

1. 第二行，因为 $FPR$ 的取值范围从 0 到 1，对应着阈值是从大到小的变化。可以从动图中看出，只不过动图中阈值是从小到大，$FPR$ 是从 1 到 0。
2. 第五行，$f_0(t)$ 的含义就是该样本为负例，得分为 $t$ 的概率。加引号是为了和正例区分。
3. 第七行，该积分相当于是遍历阈值 $t$，同时负例得分和 $t$ 相同，也就是负例遍历所有可能的得分情况。

最终得到这么一个结论：

AUC 的值，就是从样本中任意取一个正例和一个负例，正例得分大于负例得分的概率。

5. AUC 的一些性质

从公式可以看出，$TPR$ 的计算只局限在正例中，$FPR$ 的计算只局限在负例中。正例（或负例）如果同分布的增加或者减小，对于 ROC 曲线来说没有区别，因为在正例（或负例）内部已经做了归一化。如下图所示。

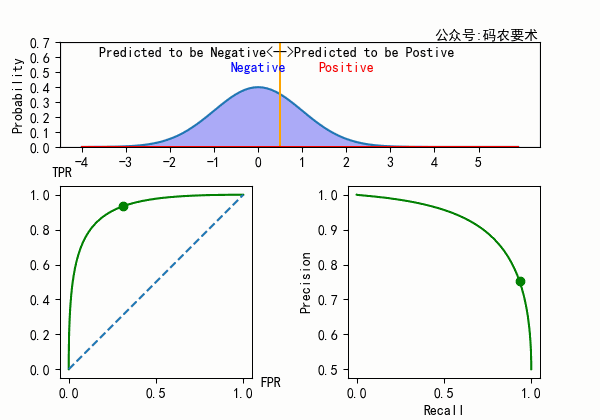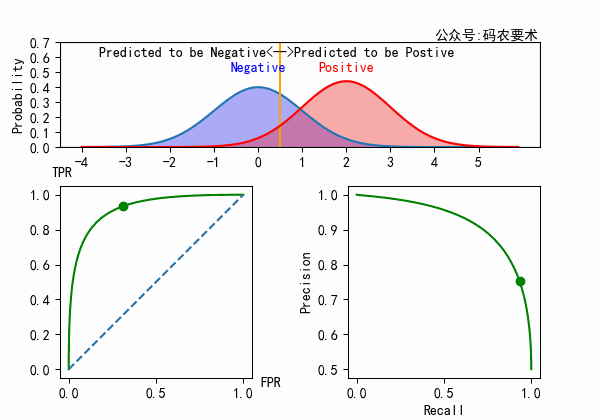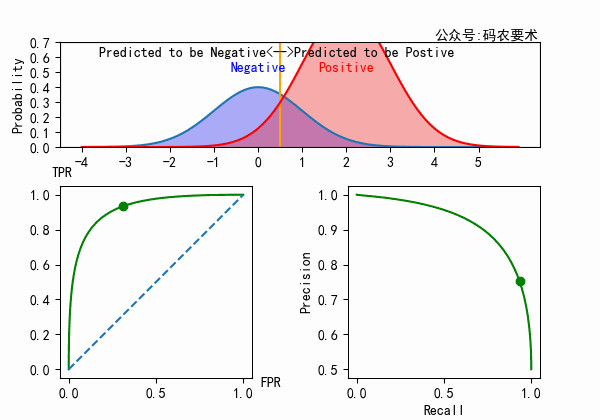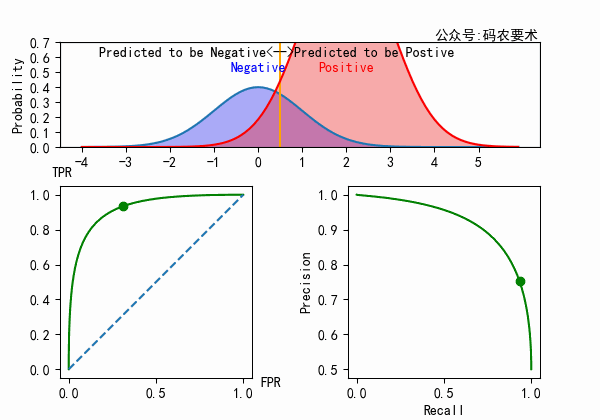
但如果正例（或负例）的比例在变化的同时，分布也发生了变化，那么 ROC 和 AUC 也会随之变化。如下图

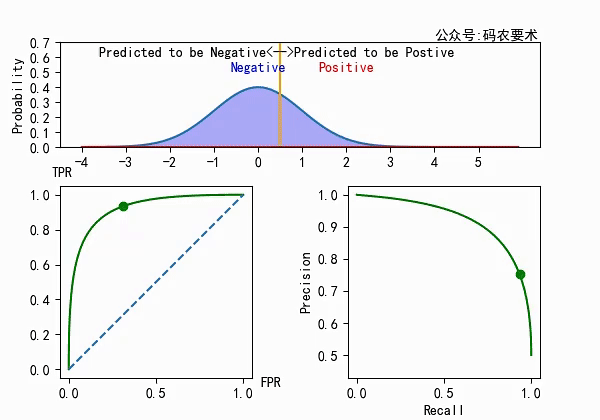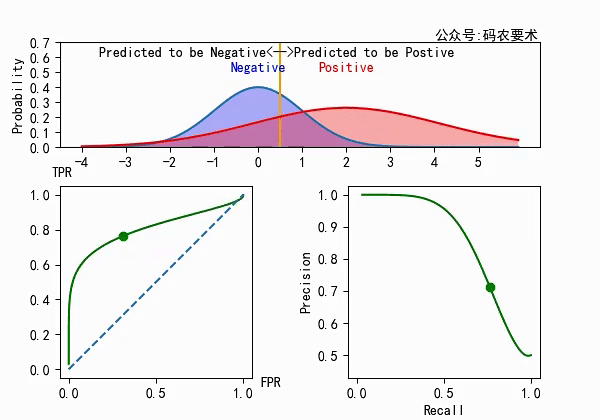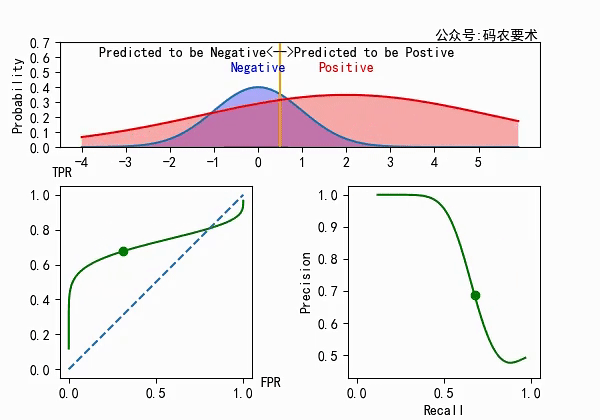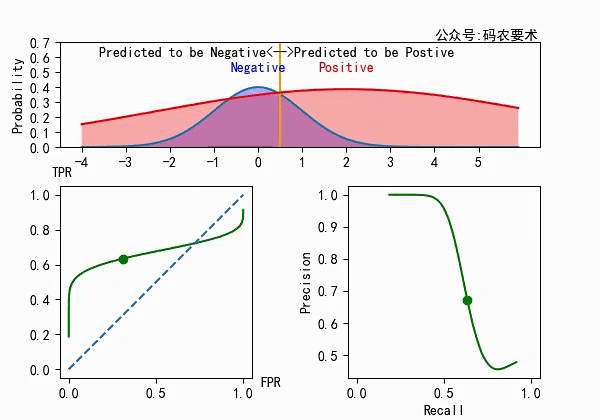
AUC 使用时，有几点需要注意：

1. AUC 只关注预测的正负例的顺序关系，对于和 label 的拟合情况则不关注。比如正例得分都是 0.2，负例得分都是 0.1，AUC 很完美，但是 loss 就会比较大。
2. 在非常不均衡的样本上，AUC 表现可能很好，但 precision 可能比较差。比如 $TP=80$，$FN=20$，$FP=200$，$TN=8000$，此时从 ROC 空间上看，效果还不错，但是 precision 低的可怜。