
分治算法(divide and conquer)是一种解决大问题的策略,通过:
- 将一个大问题分解成小问题
- 解决小问题
- 蒋小问题的解合并在一起得到想要的答案
分治思想通常应用在递归函数上。下面我们以一个数组的排序问题进行介绍。
给定一个数组

将数组分解
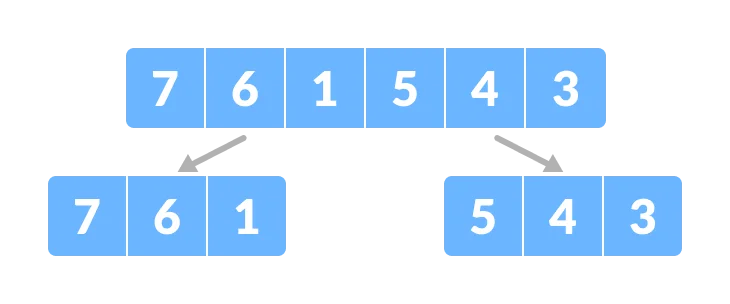
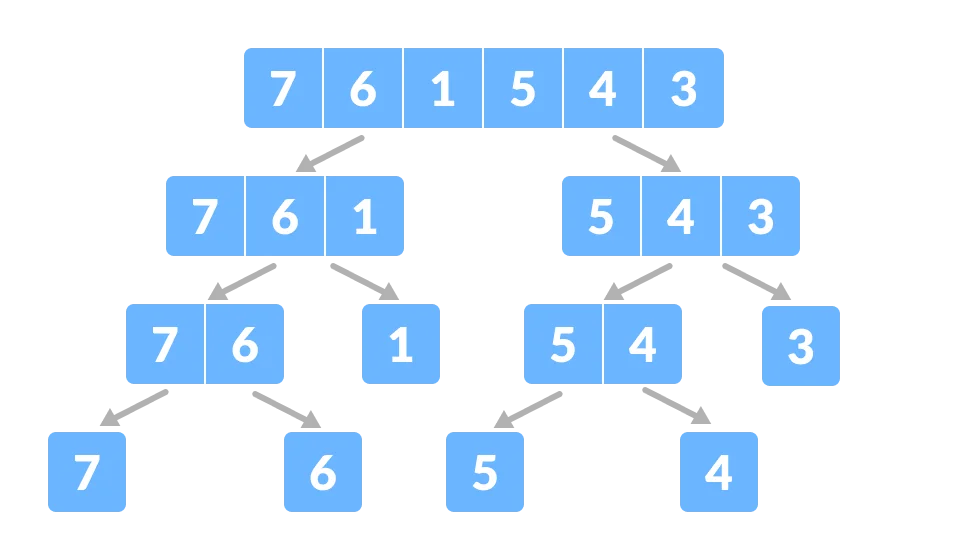
将子问题继续分解,直到每个分支只有一个元素
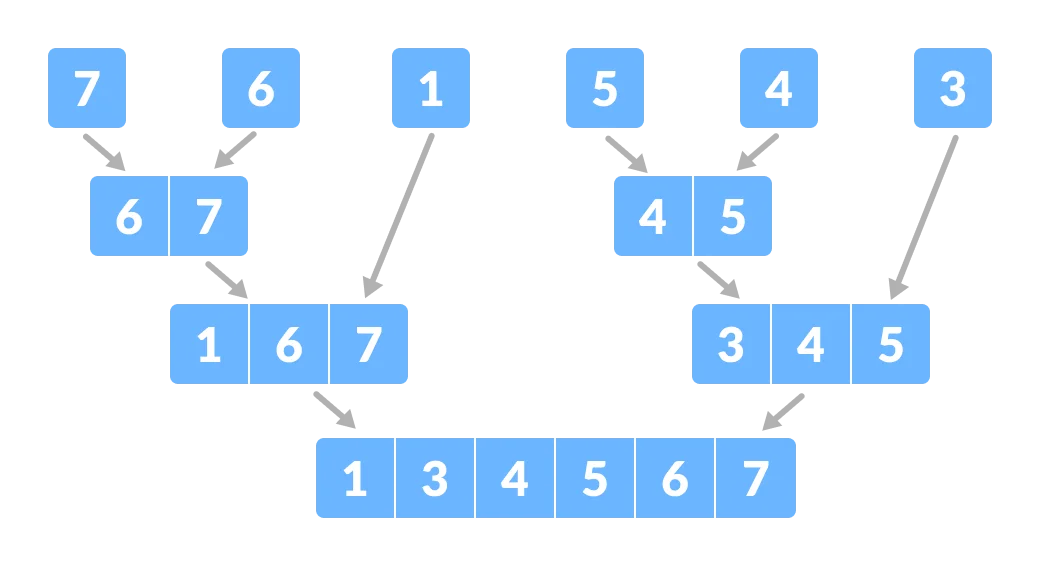
对分解后的元素进行排序,然后合并排序结果。这里我们边排序边合并。
时间复杂度
以合并排序算法为例,根据主定理:
$T(n)=aT(n/b)+f(n)=2T(n/2)+O(n)$
- $a=2$:每次将问题分解成两个子问题;
- $b=2$:每个子问题的规模是输入数据的一半;
- $f(n)=n$:分解和合并子问题的复杂度是线性增加的;
- $\log_ba=1 \Rightarrow f(n)=n^1=n$;
- 由主定理可得:$T(n)=O(n\log n)$



