评估一个模型的好坏有很多指标，每个指标都有其优缺点。如何针对不同场合选取合适的评估指标是一个非常重要的工作。本文将会介绍一些用于分类模型的评估指标，然后介绍我们该如何选取。

1. 混淆矩阵（Confusion Matrix）

混淆矩阵（混淆表）是一个用来评估分类模型的 $N\times N$ 矩阵，其中 $N$ 表示类别数量。混淆矩阵通过对比真实的类别标签和模型预测的类别标签从整体上对模型进行评估。

1.1 二分类混淆矩阵

对于二分类问题，混淆矩阵是一个 $2 \times 2$ 的矩阵，如下所示：

  • 目标标签有两个类别：Positive 和 Negative
  • 每一列表示真实的标签类别（actual values）
  • 每一行表示模型预测的标签类别（predicted values）

矩阵中的 TP、TN、FP、FN 分别表示什么呢？

True Positive（TP）

  • 模型预测的标签和真实的标签相同
  • 真实的标签是 Positive，模型预测的标签也是 Positive

True Negative（TN）

  • 模型预测的标签与真实的标签相同
  • 真实的标签是 Negative，模型预测的标签也是 Negative

False Positive（FP）

  • 模型预测的结果与真实的标签不一致
  • 真实的标签是 Negative，但模型预测的是 Positive
  • 这种错误称之为 “第一类错误”（Type-I error）

False Negative（FN）

  • 模型预测的结果与真实的标签不一致
  • 真实的标签是 Positive，但模型预测的是 Negative
  • 这种错误称之为 “第二类错误”（Type-II error）

举例说明：假设有 1000 个样本，分类模型在这些样本上得到了下面这个混淆矩阵：

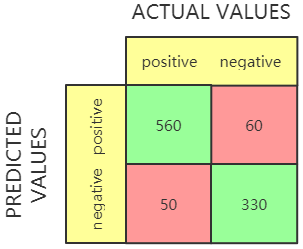
矩阵中不同的值表示：

  • True Positive (TP) = 560，有 560个 正样本被模型正确预测了；
  • True Negative (TN) = 330，有 330 个负样本被正确预测了；
  • False Positive (FP) = 60，有 60 负样本被模型预测成了正样本；
  • False Negative (FN) = 50，有 50 个正样本被模型预测成了负样本。

从混淆矩阵中可以看出，绝大多数的正样本和负样本可以被模型准确识别出来，说明这是一个还不错的分类模型。

1.2 多分类混淆矩阵

有了二分类的混淆矩阵，我们可以把它扩展到多分类问题上。假设有三个类别：A,B,C。那么混淆矩阵应该是一个 $3 \times 3$ 的矩阵：

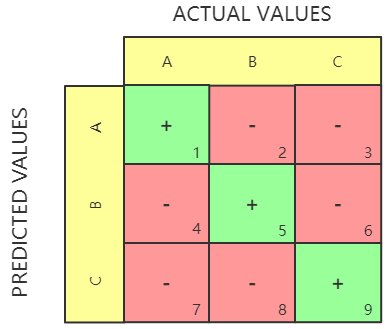
对于每个类别的 TP、TN、FP、FN 的计算方式如下：

1.3 用 scikit-learn 计算混淆矩阵

1
2
3
4
5
from sklearn.metrics import confusion_matrix

predict_class = y_pred_pos > threshold
confusion = metrics.confusion_matrix(true_class, predict_class)
print(confusion)

输出的结果如下：

1
2
[[330, 60]  
[50, 560]]

需要注意的是，scikit-learn 的混淆矩阵(0, 0) 位置是 TN，(1,1) 位置是 TP。

1.4 什么时候用？

几乎在所有的分类问题上都可以使用，尤其是在了解具体数量而非归一化的比例的时候（通常是类别不平衡）。

2. 准确率（Accuracy）

2.1 准确率定义

准确率评估的是模型对样本正确分类的比例，计算方法如下：

2.2 用 scikit-learn 计算准确率

1
2
3
4
5
6
7
8
from sklearn.metrics import confusion_matrix, accuracy_score 

y_pred_class = y_pred_pos > threshold 
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel() 
accuracy = (tp + tn) / (tp + fp + fn + tn) 

# or simply 
accuracy_score(y_true, y_pred_class)

2.3 准确率与阈值的关系

分类任务中，模型输出的是每个类别对应的概率。比如二分类，当正类别概率大于 50% 的时候，我们认为该样本是正样本，其中 50% 就是分类的阈值。阈值是可以人为设定的，比如可以规定当概率大于 70% 的时候才认为是正样本。

对于二分类模型，通常选择 0.5 作为阈值。阈值过大会造成 FN 过大，从而降低准确率。阈值太小会造成 FP 多大，同样会造成准确率过低。

2.4 什么时候用？

  • 各类别比较平衡
  • 每个类别对我们来说同等重要

2.5 什么时候不能用？

考虑一个场景：假设每 100 个人中就有 1 个人生病了，我们用一个分类模型对生病的人和没有生病的人进行分类。即使模型所有的输出都是没有生病那准确率也有 99%，但是这个模型却是很糟糕的一个模型。

仔细观察一下上面的数据分布，很容易发现问题：数据类别不平衡。也就是说，在类别不平衡的数据上评估分类模型的好坏是不可以使用准确率的。

3. 精准度（Precision）

3.1 精准度定义

精准度表示在模型预测为正样本的数据中，有多少是真正的正样本。比如用渔网捞鱼，这一网捞上来的有鱼有虾，其中是鱼的比例就是精准度。计算公式如下：

3.2 用 scikit-learn 计算精准度

1
2
3
4
5
6
7
8
from sklearn.metrics import confusion_matrix, precision_score

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
positive_predictive_value = tp/ (tp + fp)

# or simply
precision_score(y_true, y_pred_class)

3.3 精准度与阈值的关系

从这个解释中我们可以看出，阈值越高说明概率越大。从直觉上可以判断，概率越大说明可信度越高。那么样本被正确分类的可能性就越高。回到精准度的角度，精准度表示真正的正样本比例。如果阈值设定较高的话，正样本分类的正确率也会越高，精准度也会越高。极端情况下，把阈值设定成 100%，精准度也会达到最大。

3.4 什么时候用？

  • 单独使用精准度没有什么意义，通常会配合其他指标一起使用
  • 当错误警报成本过高，或者当你认为每个预测为正样本的样例都值得一看的时候，可以针对精准度进行调整

4. 召回率（Recall）

4.1 召回率定义

召回率又叫真阳性率，表示有多少是真正的正样本被模型正确识别出来了。我们经常会听到某某产品出现了质量问题，厂家紧急召回的新闻。召回率就是说，市面上所有的问题产品，厂家召回了多少。另外一个例子，目前新冠肆虐，新冠的检测是通过咽拭子。召回率表示，通过咽拭子找到了多少新冠患者。

通过这两个例子我们可以对准确率，精确度和召回率加以区分。准确率关注的是所有类别的分类正确率，精确度是正样本的准确率，而召回率表示找到的正样本占总正样本的比例。

用公式表示如下：

4.2 用 scikit-learn 计算召回率

1
2
3
4
5
6
7
8
9
from sklearn.metrics import confusion_matrix, recall_score

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
true_positive_rate = tp / (tp + fn)

# or simply

recall_score(y_true, y_pred_class)

4.3 召回率与阈值的关系

阈值设定越低，模型预测为正样本的门槛就越低，就越容易把所有的正样本找出来。所以召回率与阈值是一个负相关的关系。

4.4 什么时候用？

  • 单独使用召回率没有什么意义，通常会配合其他指标一起使用
  • 但是有些情况，比如灾难预警、欺诈性交易等，即使收到一些错误预警，我们也必须谨慎对待。即在宁可信其有不可信其无的场景下，适当调整召回率是有必要的

5. F1 得分（F1-score）

5.1 F1 得分定义

通常情况下，我们想提高精准度就需要牺牲召回率，要想提高召回率就要牺牲精准度。从之前介绍的精准度、召回率和阈值的关系中我们就可以看出一些端倪。当然，一个理想的分类模型是精准度和召回率都可以达到很高，但是实际上却是比较困难。

为了综合评估精准度和召回率，我们可以使用 F1 得分：

从定义上看，我们可以认为 F1 得分是精准度和召回率的一个平均。

5.2 用 scikit-learn 计算 F1得分

1
2
3
4
from sklearn.metrics import f1_score

y_pred_class = y_pred_pos > threshold
f1_score(y_true, y_pred_class)

在实际情况中，精准度、召回率和 F1 得分都不会单独使用，而是综合一起来评估模型的好坏：

1
2
3
4
from sklearn.metrics import classification_report

y_pred_class = y_pred_pos > threshold
classification_report(y_true, y_pred_class)

我们会得到一个类似如下的结果：

1
2
3
4
5
6
7
8
              precision    recall  f1-score   support

           1       1.00      0.67      0.80         3
           2       0.00      0.00      0.00         0

   micro avg       1.00      0.67      0.80         3
   macro avg       0.33      0.22      0.27         3
weighted avg       1.00      0.67      0.80         3

其中 support 是参与评估的总样本数，1,2,3 分别是类别标签。mirco avg，marco avg 和 weighted avg 的计算方式分别如下：

micro avg:

macro avg:

weighted avg:

假设类别 1 有 4 个，类别 2 有 10 个。

5.3 F1 得分与阈值的关系

精准度与阈值的关系是正相关，召回率与阈值的关系是负相关，F1 是精准度和召回率的综合平均值，所以当阈值过大或过小的时候都会对 F1 造成损失，所以要保证较高的 F1 得分，阈值必须在一个合理的范围内。

5.4 什么时候用？

  • F1 得分是常规分类问题的首选评估指标，但是通常也会配合准确率，精准度和召回率

6. F2 得分（F2-score）

6.1 F2 得分定义

F2 得分表示精准度和召回率的综合评价，与 F1 不同的是，F2 着重强调召回率：

6.2 用 scikit-learn 计算 F2 得分

1
2
3
4
from sklearn.metrics import fbeta_score

y_pred_class = y_pred_pos > threshold
fbeta_score(y_true, y_pred_class, 2)

6.3 F2 得分与阈值的关系

由于 F2 得分更强调召回率的作用，所以 F2 的性质也与召回率的性质相似，随着阈值的提高 F2 得分会有一个库快速的上升，然后短暂达到平衡，然后随着阈值的升高 F2 得分逐渐下降。

6.4 什么时候用？

  • 在注重召回率的场景下都可以使用

7. F-beta 得分（F-beta score）

7.1 F-beta 定义

既然有 F1 得分，有 F2 得分，那么我顶定义一个 $\beta$ ，当 $\beta=1$ 时，即为 F1 得分，当 $\beta=2$ 时，即为 F2 得分。计算方法如下：

我肯可以通过调整 $\beta$ 值来确定召回率在我们的评估指标中占有的比重。

7.2 用 scikit-learn 计算 F-beta 得分

在上面计算 F2 得分的时候，我们就可以发现，用到了 fbeta_score 函数：

1
2
3
4
from sklearn.metrics import fbeta_score

y_pred_class = y_pred_pos > threshold
fbeta_score(y_true, y_pred_class, beta)

7.3 F-beta 得分与阈值的关系

上图展示了不同 $\beta$ 值时， F-beta 与阈值的关系。

8. 假阳性率（Type-I error）

8.1 假阳性率定义

假阳性率表示，我们预测的某事但没有发生。因此，假阳性率又可以叫做误报率。比如，本来没有大雨，但是天气预报却预报说有雨，说明天气预报误报了。我们可以将其视为模型发出的错误报警。

8.2 用 scikit-learn 计算假阳性率

1
2
3
4
5
from sklearn.metrics import confusion_matrix

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
false_positive_rate = fp / (fp + tn)

8.3 假阳性率与阈值的关系

通常一个好的模型假阳性率都比较低，但是我们还可以通过调节阈值来进一步降低假阳性率。因为在分母中包含真负样本（$TN$），当我们的数据不平衡时，假阳性率通常会很低。

显然，随着阈值的增大，假阳性率在降低。

8.4 什么时候用？

  • 很少单独使用假阳性率，通常是和其他指标一起使用；
  • 如果误报会导致较严重的后果，可以通过调节阈值来降低。

9. 假阴性率（Type-II error）

9.1 假阴性率定义

假阴性率表示，当我们没有预测的事情却发生了。因此，假阴性率又可以叫做漏报率。比如，本来有一场大雨，但是天气预报没有预报，说明天气预报对这次大雨漏报了。

9.2 用 scikit-learn 计算假阴性率

1
2
3
4
5
from sklearn.metrics import confusion_matrix

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
false_negative_rate = fn / (tp + fn)

9.3 假阴性率与阈值的关系

当我们提高阈值的时候，假阴性率也会随之升高。

9.4 什么时候用？

  • 通常与其他指标一起使用；
  • 如果漏报的代价比较大的时候，就需要关注这个指标了。

10. 真阴性率（True negative rate）

10.1 真阴性率定义

真阴性率表示，在所有的负样本中有多少负样本被检测出来。

10.2 用 scikit-learn 计算真阴性率

1
2
3
4
5
from sklearn.metrics import confusion_matrix

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
true_negative_rate = tn / (tn + fp)

10.3 真阴性率与阈值的关系

阈值越高，真阴性率越高。

10.4 什么时候用？

  • 通常与其他指标一起用；
  • 当你确实希望确保你所说的每一句都是正确的时候，可以考虑该指标。比如，当一个医生对病人说 “你很健康” 的时候。

11. 负样本预测值（Negative Predictive Value）

11.1 负样本预测值定义

负样本预测值表示，模型预测的负样本有多少是真正的负样本，我们可以认为它是负类别的准确率。

11.2 用 scikit-learn 计算负样本预测值

1
2
3
4
5
from sklearn.metrics import confusion_matrix

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
negative_predictive_value = tn/ (tn + fn)

11.3 负样本预测值与阈值的关系

阈值越高就会有越多的样本被预测为负样本，被误分类成负样本的几率就越高。但是对于非平衡数据集来说，一个较高的阈值通常负样本预测值表现也还不错。

11.4 什么时候用？

  • 当我们更加关注负样本的预测准确率时，可以考虑使用这一评估指标。

12. 假发现率（False Discovery Rate）

12.1 假发现率定义

假发现率表示，所有预测为正样本的数据中有多少是真正的正样本。

12.2 用 scikit-learn 计算假发现率

1
2
3
4
5
from sklearn.metrics import confusion_matrix

y_pred_class = y_pred_pos > threshold
tn, fp, fn, tp = confusion_matrix(y_true, y_pred_class).ravel()
false_discovery_rate = fp/ (tp + fp)

12.3 假发现率与阈值的关系

阈值越高，假发现率越低。

12.4 什么时候用？

  • 通常和其他指标一起使用；
  • 如果误报的代价过高，或者当你希望所有预测为正样本的数据都值得一看的时候，可以考虑该指标。

13. Cohen Kappa Metric

13.1 Cohen Kappa 定义

简单来说，Cohen Kappa 指的是你的模型比一个随机分类器好多少。

  • $p_0$ 表示模型预测结果，通常为准确率；
  • $p_e$ 表示随机预测结果，通常为随机模型的准确率。

13.2 用 scikit-learn 计算 Cohen Kappa

1
2
3
from sklearn.metrics import cohen_kappa_score

cohen_kappa_score(y_true, y_pred_class)

13.3 Cohen Kappa 与阈值的关系

13.4 什么时候用？

  • Cohen Kappa 通常不会用在一般的文本分类上，而是在非平衡数据的分类模型上。

14. Matthews Correlation Coefficient （MCC）

$MCC$ 表示真实标签和预测标签的相关性。

14.1 MCC 定义

14.2 scikit-learn 计算 MCC

1
2
3
4
from sklearn.metrics import matthews_corrcoef

y_pred_class = y_pred_pos > threshold
matthews_corrcoef(y_true, y_pred_class)

14.3 MCC 与阈值的关系

14.4 什么时候用？

  • 不平衡数据集
  • 希望预测结果有更强的可解释性的

15. ROC 曲线

ROC 曲线是一个图表，用于展示真阳性率（$TPR$）和假阳性率（$FPR$）之间的权衡。基本上，对于每个阈值，我们计算 $TPR$ 和 $FPR$ 并将其绘制在一张图表上。它代表的是分类器以多大的置信度将样本分类为正样本。

可以在 Tom Fawcett 的这篇文章中找到对 ROC 曲线和 ROC AUC 分数的广泛详细的讨论。

15.1 用 scikit-learn 计算 ROC

1
2
3
4
from scikitplot.metrics import plot_roc

fig, ax = plt.subplots()
plot_roc(y_true, y_pred, ax=ax)

15.2 曲线图是什么样的？

每个不同的阈值对应曲线上不同的点（即不同的混淆矩阵）。对于每个阈值，较高的 $TPR$ 和较低的 $FPR$ 越好，因此具有更多左上角曲线的分类器更好。从上图可以看出，在大约（0.15， 0.85）左右的位置（左上角黑色实线和黑色虚线焦点）二者取得平衡。因此该位置对应的阈值应该是最佳的分类阈值。

16. ROC-AUC 得分

为了从 ROC 曲线上得到一个量化的指标，我们可以计算 ROC-AUC（Area Under the ROC Curve） 得分。

16.1 用 scikit-learn 计算 ROC-AUC

1
2
3
from sklearn.metrics import roc_auc_score

roc_auc = roc_auc_score(y_true, y_pred_pos)

16.2 什么时候用？

  • 当你非常关心排序预测的时候，应该使用 ROC-AUC 得分而没有必要关注概率修正。
  • 当你的数据严重不平衡的时候，不应该使用 ROC-AUC 作为评估指标。直观上来讲，当数据严重类别不平衡的时候， $FPR$ 会被严重拉低，因为大量的数据是 True Negative 的。
  • 当正负样本的类别平衡的时候，可以使用 ROC-AUC 作为评估指标。

17. Precision-Recall Curve

PRC 是一条融合了精准度和召回率的可视化曲线。对于每个阈值，计算相应的精准度和召回率，然后画在图上即可。Y 轴对应的值越高，则模型表现越好。

17.1 用 scikit-learn 计算 PRC

1
2
3
4
from scikitplot.metrics import plot_precision_recall

fig, ax = plt.subplots()
plot_precision_recall(y_true, y_pred, ax=ax)

17.2 曲线长什么样？

18. PR AUC 得分 | 平均精准度

与 ROC-AUC 类似，我们也可以计算 Area Under the Precision-Recall Curve 以获得评估模型的量化指标。

18.1 用 sickit-learn计算 PR AUC

1
2
3
from sklearn.metrics import average_precision_score

average_precision_score(y_true, y_pred_pos)

18.2 什么时候用？

  • 当你要在精准度和召回率之间做取舍的时候
  • 当你要选择一个合适的阈值符合实际情况的时候
  • 当你的数据严重不平衡的时候。就像之前讨论的那样，由于 PR AUC 主要关注点是正样本的类别，很少关注到负样本。所以在类别严重不平衡的时候可以使用 PR AUC 作为模型的评估指标。
  • 当你更关注正样本而非负样本的时候，可以使用 PR AUC 作为模型的评估指标。

19. Log loss

对数损失函数经常用来优化机器学习模型的参数。然后实际上它也可以作为模型的评估指标。

19.1 定义对数损失

对数损失用来计算真实标签与预测标签之间的差别：

观测到的正样本置信度越高，那么它与真实的正样本之间的差距就越小。但是这并不是一个线性关系，真实的关系如下图：

19.2 用 scikit-learn 计算对数损失

1
2
3
from sklearn.metrics import log_loss

log_loss(y_true, y_pred)

19.3 什么时候用？

  • 几乎总是有一个性能指标可以更好地匹配我们的业务问题。 因此，我们可以使用对数损失作为模型的目标，并使用其他一些指标来评估性能。

20. Brier 得分

20.1 Brier 得分定义

20.2 用 scikit-learn 计算 Brier 得分

1
2
3
from sklearn.metrics import brier_score_loss

brier_score_loss(y_true, y_pred_pos)

20.3 什么时候用？

  • 当你关心修正概率的时候

21. 累积收益表

21.1 定义累积收益表

简单来说，累积收益表（Cumulative gains chart）可以帮助我们判断使用当前模型的收益超过一个随机模型多少。

  • 先对预测结果从高到低进行排序
  • 对于每个百分数，我们计算大于这个百分数的真阳性样本比例。

21.2 用 scikit-learn 计算 CGC

1
2
3
4
from scikitplot.metrics import plot_cumulative_gain

fig, ax = plt.subplots()
plot_cumulative_gain(y_true, y_pred, ax=ax)

21.3 CGC 看起来是什么样的？

21.4 什么时候用？

  • 当你想选择最有希望与你进行交易的客户的时候，可以使用 CGC 作为评估指标。
  • 它可以作为 ROC-AUC 指标的一个很好的额外补充。

22. Lift curve | lift chart

22.1 定义 lift curve

Lift curve 基本上只是 CGC 的另一种表示形式：

  • 首先对预测结果由高到低进行排序；
  • 对于每个预测值，计算训练好的模型和随机模型达到该百分比概率的真阳性比例
  • 计算上述比例，然后画图

它能告诉我们对于给定最大预测值，它比一个随机模型好多少。

22.2 用 scikit-learn 计算 lift curve

1
2
3
from scikitplot.metrics import plot_lift_curve 

fig, ax = plt.subplots() plot_lift_curve(y_true, y_pred, ax=ax)

22.3 什么时候用？

  • 当你想选择最有希望与你进行交易的客户的时候，可以使用 CGC 作为评估指标。
  • 它可以作为 ROC-AUC 指标的一个很好的额外补充。

23. Kolmogorov-Smirnov plot

23.1 定义 KS plot

KS plot 帮助我们从预测结果中获得独立的正样本分布和负样本分布。

  • 根据预测得分进行排序
  • 对 [0.0, 1.0] 之间的每个截点计算相邻截点（depth）之间的数据中的真阳性和真阴性比例
  • 画出计算出来的比例，y 轴表示 $positive(depth)/positive(all)$，$negative(depth)/negative(all)$，x 轴表示 depth

KS plot有点类似于 CGC，但是CGC 只关注正样本，而 KS plot同时关注正负样本。

23.2 用 scikit-learn 计算 KS plot

1
2
3
4
from scikitplot.metrics import plot_ks_statistic

fig, ax = plt.subplots()
plot_ks_statistic(y_true, y_pred, ax=ax)

24. Kolmogorov-Smirnov statistic

24.1 定义 KS statistic

如果我们想从 KS plot 中选择一个值作为指标，那么我们可以查看所有 KS plot 中所有阈值，然后找到正负样本分布距离最远的点。

如果有一个阈值，所有观测到的上方样本都是真阳性，而所有下方的样本都是真阴性，那么我们就找到了一个完美的 KS statistic 值：1.0

24.2 用 scikit-learn 计算 KS statistic

1
2
3
4
from scikitplot.helpers import binary_ks_curve

res = binary_ks_curve(y_true, y_pred_pos)
ks_stat = res[3]

24.3 什么时候用？

  • 当你面对的是排序问题且你对正负样本都很关心的时候
  • 可以作为 ROC-AUC 的补充指标

参考资料

  1. 24 Evaluation Metrics for Binary Classification (And When to Use Them)
  2. Everything you Should Know about Confusion Matrix for Machine Learning
 上一页

算法 divide-conquer

 评论