数据结构与算法：时间复杂度

就像做菜有好吃和不好吃一样，算法也有好的算法和不好的算法。那么我们怎么评价一个算法的好坏呢？

1. 时间复杂度

时间复杂度是用来估算算法需要执行的时间的。但是我们并不是直接用时间来估计，而是用一个函数。

时间复杂度不是算法需要执行多久，而是算法需要执行多少步。

这种评估方法看起来很奇怪，为什么不直接用时间来评估呢？很显然，一个需要 10 秒的的算法肯定是不如只需要 1 秒的算法啊。事实并非如此，比如同一个排序算法，对 100 个元素进行排序和对 1000 个元素进行排序所用时间肯定是不同的，能说算法变坏了吗？算法运算的时间依赖于输入参数的大小。

如果一个排序算法的输入本来就已经排好了序，那么它的运算时间肯定要比乱序输入更快。即使输入参数大小相同，算法的运算时间也会有差异。

另外，CPU 运算波动，磁盘读写效率等等都会影响算法的运算时间。

所以，即使是同一个算法，它的运算时间也会有：

• 最长运算时间
• 最短运算时间
• 平均运算时间

而我们通常关心的是一个算法的最长运算时间（抱最好的希望，做最坏的打算）。所以我们对算法性能的分析要包含两方面的考虑：

1. 忽略掉依赖于机器的因素；
2. 关注运行时间的增长，而不是去检查真正的运行时间.

1.1 计算时间复杂度

举个例子：找到一个数组中的最小数字。

第一步：开始
第二步：声明变量 min
第三步：从输入数组中循环取值
      3.1 对比从数组中取到的值 n 和 min 的大小
      3.2 如果 n < min
      3.3 令 min = n
第四步：返回 min 的值

假设 cpu 的运算是平稳没有波动的，每一步所需的时间相同。我们来看下上面的过程：

• 第一步：1 个操作；
• 第二步：1 个操作
• 第三步：这一步需要执行 $m$ （数组中有 $m$ 个元素）次，假设每一小步是 1 个操作，每一次循环就需要 4 个操作，那么这个循环就相当于需要 $4m$ 个操作
• 第四步： 1 个操作

总共需要 $4m+3$ 个操作。但是这个表达式太过于具体了，不能对比不同的算法。我们需要进一步简化时间复杂度的计算。

1.2 渐进分析

1.2.1 符号表示

为了更方便表示时间复杂度，我们使用渐进符号来表示。主要有三种符号：

• $O$ 符号：表示算法运算的上限，即表现最差的运算时间。

  

  $$O(g(n)) = \{f(n) ~|~ \exists c>0, ~ n \ge n_0,~ 0\le f(n)\le cg(n) \}$$

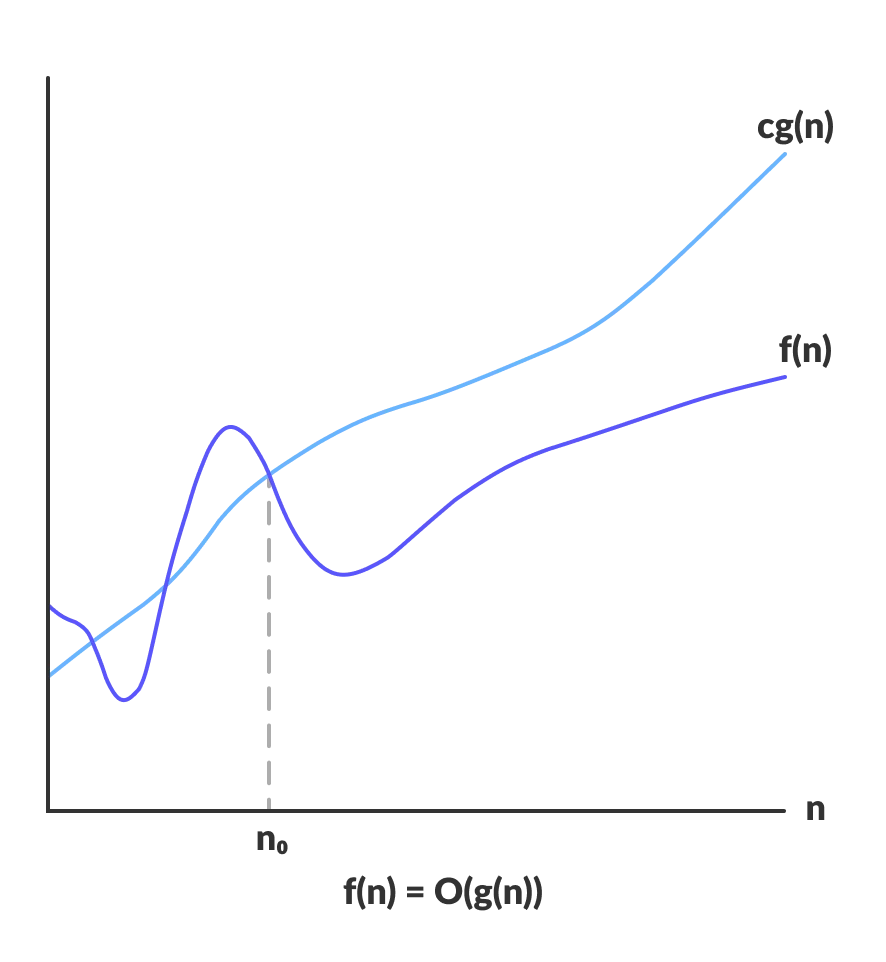
  $O(g(n))$ 是函数 $f(n)$ 的集合。$f(n)$ 满足以下条件：存在一个正实数 $c$，使得当 $n$ 足够大时（大于一个阈值 $n_0$） ，所有的 $f(n)$ 都小于 $cg(n)$。

• $\Omega$ 符号：表示算法运算下限，即表现最好的运算时间。

  

  $$\Omega(g(n)) = \{f(n)~ \vert ~ \exists c>0,~ n\ge n_0,~ 0 \le f(n) \le cg(n) \}$$

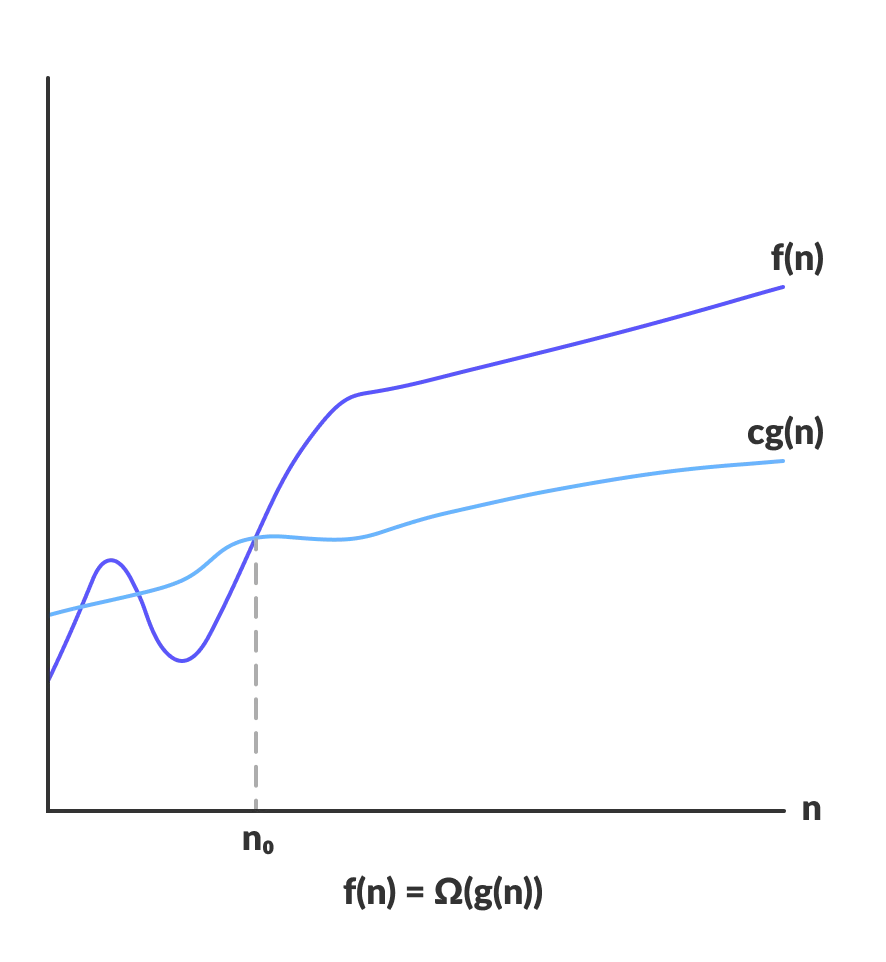
  $\Omega(g(n))$ 是函数 $f(n)$ 的集合。$f(n)$ 满足以下条件：存在一个正实数 $c$，使得当 $n$ 足够大时（大于一个阈值 $n_0$），所有的 $f(n)$ 都大于 $cg(n)$。

• $\Theta$ 符号：表示算法运算时间的平均水平，即平均运算时间。

  

  $$\Theta(g(n)) = \{f(n)~ \vert ~ \exists c_1,c_2>0,~ n \gt n_0,~ 0 \le c_1g(n) \le f(n) \le c_2g(n)\}$$

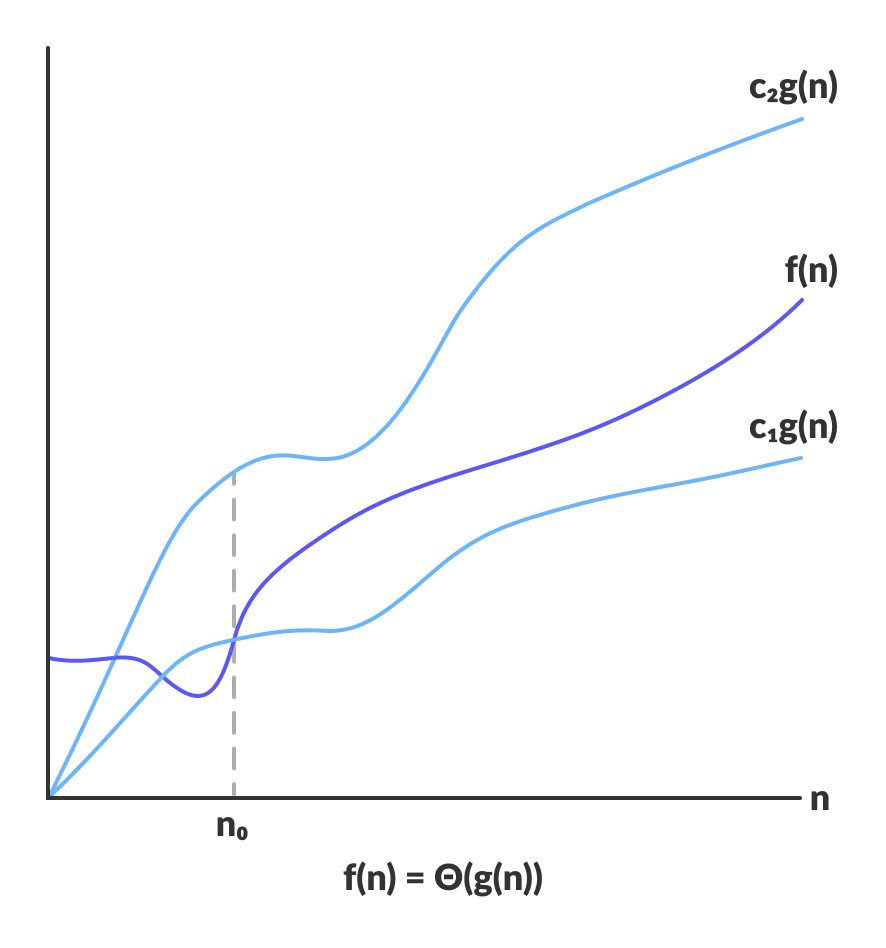
  $\Theta(g(n))$ 是函数 $f(n)$ 的集合。$f(n)$ 满足以下条件：存在正实数 $c_1,c_2$，使得当 $n$ 足够大时（大于一个阈值 $n_0$），所有的 $f(n)$ 都介于 $c_1g(n)$ 和 $c_2g(n)$ 之间。

1.2.2 渐进分析

渐进分析遵循三个原则：

• 分析最坏的情况，即 $O(g(n))$。
• 不关心系数和低阶项。从上面我们对 $O(g(n))$ 的定义可以看出，系数相当于 $c$，而我们关心的是 $g(n)$。如前所说，对时间复杂度的分析更关注的是运行时间的增长。当 $n$ 足够大的时候，低阶项对运行时间的增长影响力越来越低，所以也不是我们关心的点。
• 分析当 $n$ 足够大的时候的运行时间。

渐进分析是将时间复杂度函数做无穷近似。比如上面的例子中 $4m+3$ 可以泛化成 $km+c$。忽略掉系数 $k$ 和低阶项 $c$，所以上面的算法时间复杂度为 $O(m)$。

$O$ 表示方程的阶（order）。常见的时间复杂度及其对比：

$n$	$O(1)$	$O(\log n)$	$O(n)$	$O(n \log n)$	$O(n^2)$	$O(2^n)$
1	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec
10	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec
100	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	40170 trillion years
1,000	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	> vigintillion years
10,000	< 1 sec	< 1 sec	< 1 sec	< 1 sec	2 min	> centillion years
100,000	< 1 sec	< 1 sec	< 1 sec	1 sec	3 hours	> centillion years
1,000,000	< 1 sec	< 1 sec	1 sec	20 sec	12 days	> centillion years

1.3 非递归算法

非递归算法时间复杂度计算步骤如下：

1. 找到问题的输入数据规模，比如 2.1 节中的 $m$；
2. 找出算法的基本操作，比如 2.1 节中的循环操作；
3. 建立算法中涉及到的操作数求和表达式；
4. 利用 $O$ 准则进行简化。

具体例子可以看 2.1 节的例子。

1.4 递归算法

递归算法的时间复杂度有两种方法进行计算：

• 迭代法：每次运算只是将数据规模减一，比如斐波那契数列；
• 主定理：利用分治的思想，将问题拆解成几份，分别求解。

1.4.1 迭代法

以斐波那契数列为例：

第一步：定义函数 fab(n)
第二步：判断 n 是否为 0
第三步：如果 n == 0，返回 1
第四步：如果 n != 0, 返回 fab(n-1) * n

假设 fab(n) 需要执行 $C(n)$ 次，$C(n)$ 的计算公式为：

$$C(n) = C(n-1)+1$$

$C(n-1)$ 为 fab(n-1) 的运算次数，当 $n=0$ 时，fab(0) 直接返回值，所以只需要运算 1 次，即 $C(0)=1$。

$$\begin{equation} \nonumber \begin{aligned} C(n) &= C(n-1)+1\\\\ &= [C(n-2)+1]+1\\\\ &= [C(n-3)+1]+2\\\\ & \dots \\\\ &= C(n-i)+i \\\\ & \dots \\\\ &= C(n-n)+n \\\\ &= n \end{aligned} \end{equation}$$

所以这个算法的时间复杂度为 $O(n)$。

1.4.2 主定理

当我们使用分治思想求解递归问题的时候，就可以用“主定理”（master theorem）的方法来计算时间复杂度。具体来说，当递归函数的时间复杂度计算公式满足：

$$T(n)=aT(\frac{n}{b})+f(n)$$

其中：

• $n$：输入数据规模
• $a$：将递归问题分解成子问题的个数
• $n/b$：每个子问题的规模，
• $f(n)$：递归操作之外所需要的操作次数，包括问题分解和结果合并

$a$ 和 $b$ 是大于 $0$ 的常数，$f(n)$ 是渐进函数，即当 $n \to \infty$ 时 $f(n)>0$。

上面的公式可以理解为：对于一个规模为 $n$ 的问题，我们把它分解成 $a$ 个子问题，每个子问题规模为 $n/b$ 指的是 $\lfloor{n/b}\rfloor$ 或者 $\lceil{n/b}\rceil$（$\lfloor \cdot \rfloor$ 表示是向下取整，$\lceil \cdot\rceil$ 表示向上取整），然后将问题的解通过 $f(n)$次操作整合到一起。

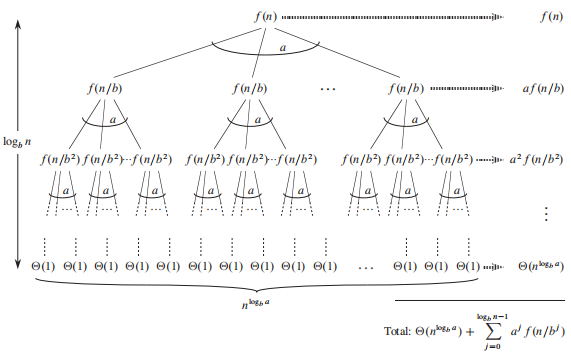
首先构建一棵递归任务分解树，观察每一层的变化：

第一层：

• 子问题的数目：$a^0$

• 每个子问题的规模：$\frac{n}{b^0}$

• 合并子问题需要花费的操作次数：$f(n)$

第二层：

• 子问题的数目：$a^1$
• 每个子问题的规模：$\frac{n}{b^1}$
• 合并子问题需要花费的操作次数：$af(n/b)$

第三层：

• 子问题的数目：$a^2$
• 每个子问题的规模：$\frac{n}{b^2}$
• 合并子问题需要花费的操作次数：$a^2f(n/b^2)$

…

最后一层：

• 子问题的数目：$a^2$
• 每个子问题的规模：$\frac{n}{b^h}$
• 合并子问题需要花费的操作次数：$a^hf(n/b^h)$

• NOTE

第一层，“合并子问题需要花费的操作次数”，实际上指的是要解决一个和原问题等规模的问题所需要的操作次数。因为第一层还没有对问题进行分解，也就谈不上合并子问题，上面的说法只是为了和下面保持一致。

• 树的高度 $h$

  对于分治递归方法，最后一层的每个子问题规模为 1，即 $\frac{n}{b^h}=1$，由此可得

  $$h = \log_b n$$

• 叶子结点个数

  叶子结点的个数即为最后一层子问题的数目 $a^h$。由上一步 $h = \log_b n$ 可得，叶子结点的个数为 $a^{\log_b n}$。根据换底公式 $x^{\log_ny}=y^{\log_nx}$ 可以将上式改写成 $n^{\log_ba}$。注意每个子问题的划分都是 $n/b$ 的均匀划分，所以时间复杂度也应该用 $\Theta$ 表示，即

  $$\Theta(n^{\log_ba})$$

• 合并子问题需要花费的操作次数总和

  根据我们对每层递归树的分析可以发现，每层合并子问题需要的操作次数为 $a^if\Big(\frac{n}{b^i}\Big)$，只需要将每层次数相加即可得到总次数：

  $$\sum_{i=0}^{\log_bn-1}a^if\Big(\frac{n}{b^i}\Big)$$

有了递归操作总次数和分解合并操作总次数以后，根据递归函数时间复杂度公式可得

$$\begin{equation} \nonumber \begin{aligned} T(n) &= aT(\frac{n}{b})+f(n) \\\\ &= \Theta(n^{\log_ba})+\sum_{i=0}^{\log_bn-1}a^if\Big(\frac{n}{b^i}\Big) \\\\ &= \Theta(n^{\log_ba})+g(n) \end{aligned} \end{equation}$$

从中我们可以看出，整个递归的时间复杂度取决于 $f(n)$，分三种情况讨论：

1. 如果右边第一项的阶数比第二项高， $T(n)$ 主要由第一项决定，这意味着递归树的时间主要消耗在子问题的递归上。根据时间复杂度分析“忽略低阶项”的原则：

   $$T(n) = \Theta(n^{\log_ba})$$

2. 如果右边第二项的阶数比第一项高， $T(n)$ 主要由第二项决定，这意味着递归树的时间主要消耗在对问题的分解和解的合并上，根据时间复杂度分析“忽略低阶项”的原则：

   $$T(n) = \Theta(f(n))$$

3. 如果两部分的阶数相等，意味着递归树的总时间分布是均匀的，由两部分共同决定：

   $$T(n)=\Theta(n^{\log_b a} \cdot \log n)$$

1.4.3 主定理证明

为了方便写证明过程，将以上三种情况用数学语言进行描述：

1. $\exists \epsilon>0 s.t. f(n)=O(n^{\log_ba-\epsilon})$，则 $T(n)=\Theta(n^{\log_ba})$。

   证明：

   $$\begin{equation} \nonumber \begin{aligned} f(n) &= O(n^{(\log_ba)-\epsilon}) \\\\ \Rightarrow f(\frac{n}{b^i}) &= O((\frac{n}{b^i})^{(\log_ba)-\epsilon}) \\\\ &\le c(\frac{n}{b^i})^{(\log_ba)-\epsilon} \\\\ \Rightarrow a^if(\frac{n}{b^i}) &\le c a^i(\frac{n}{b^i})^{(\log_ba)-\epsilon} \\\\ &= cn^{(\log_ba)-\epsilon} \cdot (\frac{a}{b^{(\log_ba)-\epsilon}})^i\\\\ &= cn^{(\log_ba)-\epsilon} \cdot (\frac{a}{a^{(\log_bb)}\cdot b^ {-\epsilon}})^i\\\\ &= cn^{(\log_ba)-\epsilon} \cdot (b^\epsilon)^i \\\\ \Rightarrow \sum_{i=0}^{\log_bn-1}a^if\Big(\frac{n}{b^i}\Big) &\le \sum_{i=0}^{\log_bn-1} cn^{(\log_ba)-\epsilon} \cdot (b^\epsilon)^i \\\\ &= cn^{(\log_ba)-\epsilon} \cdot \sum_{i=0}^{\log_bn-1}(b^\epsilon)^i\\\\ &= cn^{(\log_ba)-\varepsilon} \cdot \frac{(b^\varepsilon)^{\log_bn}-1}{b^\varepsilon-1} \\\\ &= cn^{(\log_ba)-\varepsilon} \cdot \frac{n^\epsilon-1}{b^\epsilon-1} \\\\ &= \frac{c}{b^\epsilon-1} \left[ n^{\log_ba}-n^{(\log_ba)-\epsilon} \right] \\\\ &= O(n^{\log_ba}) \end{aligned} \end{equation}$$

   由此可得

   $$T(n) =\Theta(n^{\log_ba}) +O(n^{\log_ba})$$

   由于上式右侧两部分的函数增长率相同，所以

   $$T(n) = \Theta(n^{\log_ba})$$

   个人理解是，$\Theta$ 表示的是平均水平，即它可能有更高的上限和更低的下限。而 $O$ 已经是上限了，当 $\Theta$ 取上限的时候，阶数是要比 $O$ 更高的。所以，当 $\Theta$ 和 $O$ 的增长率是相同的时候，复杂度取 $\Theta$。

2. $\exists \epsilon>0 s.t. f(n)=\Omega(n^{\log_ba+\epsilon})$，且 $\exists c<1$。当 $n \to \infty$， $a\, f(\frac{n}{b})\le c\, f(n)$。此时 $T(n)=\Theta(f(n))$。

   证明：

$$\begin{equation} \nonumber \begin{aligned} af(\frac{n}{b}) &\le cf(n) \\\\ \Rightarrow f\Big(\frac{n}{b}\Big) &\le \frac{c}{a}f(n)\\\\ \Rightarrow f\Big(\frac{n}{b^2}\Big) &\le \frac{c}{a}f\Big(\frac nb\Big)\le\Big(\frac{c}{a}\Big)^2f(n)\\\\ &\vdots\\\\ f\Big(\frac{n}{b^i}\Big) &\le\Big(\frac{c}{a}\Big)^if(n)\\\\ \Rightarrow a^i\, f\Big(\frac{n}{b^i}\Big) &\le c^i\, f(n)\\\\ \Rightarrow g(n) &\le f(n)\sum_{i=1}^{\log_bn-1}\\\\ &\le f(n)\sum_{i=1}^\infty c^i\\\\ &= \frac{1}{1-c}f(n)\\\\ \Rightarrow g(n) &= O(f(n))\\\\ g(n) &= f(n) + af(\frac{n}{b})+ \dots + a^{\log_bn-1}f(\frac{n}{b^{\log_bn-1}}) \\\\ &\ge f(n)\\\\ \Rightarrow g(n) &= \Omega(f(n)) \end{aligned} \end{equation}$$

由 $g(n)=O(f(n))$ 和 $g(n)=\Omega(f(n))$ 可得：

$$g(n) = \Theta(f(n))=\Theta(n^{\log_ba+\epsilon})$$

此时

$$T(n) = \Theta(n^{\log_ba})+\Theta(n^{\log_ba+\epsilon})$$

后者的阶数更高，所以

$$T(n) = \Theta(f(n))$$

1. 如果 $f(n)=\Theta(n^{\log_ba})$，则 $T(n)=\Theta(n{\log_ba}\cdot\log n)$。

证明：

$$\begin{equation} \nonumber \begin{aligned} f(n) &= \Theta(n^{\log_ba}) \\\\ \Rightarrow f(\frac{n}{b^i}) &= \Theta((\frac{n}{b^i})^{\log_ba}) \\\\ \Rightarrow c_1(\frac{n}{b^i})^{\log_ba} &\le f(\frac{n}{b^i}) \le c_2(\frac{n}{b^i})^{\log_ba}\\\\ \Rightarrow a^i \cdot c_1(\frac{n}{b^i})^{\log_ba} &\le a^i \cdot f(\frac{n}{b^i}) \le a^i\cdot c_2(\frac{n}{b^i})^{\log_ba}\\\\ \Rightarrow c_1n^{\log_ba}(\frac{a}{b^{\log_ba}})^i &\le a^if(\frac{n}{b^i})\le c_2n^{\log_ba}(\frac{a}{b^{\log_ba}})^i\\\\ c_1n^{\log_ba}(1)^i &\le a^if(\frac{n}{b^i})\le c_2n^{\log_ba}(1)^i\\\\ \sum_{i=0}^{\log_bn-1} c_1n^{\log_ba}(1)^i &\le \sum_{i=0}^{\log_bn-1}a^if(\frac{n}{b^i})\le \sum_{i=0}^{\log_bn-1} c_2n^{\log_ba}(1)^i\\\\ c_1n^{\log_ba}\cdot \log_bn &\le g(n) \le c_2n^{\log_ba} \\\\ c_1n^{\log_ba}\frac{\log n}{\log b} &\le g(n) \le c_2 n^{\log_ba} \frac{\log n}{\log b}\\\\ \frac{c_1}{\log b} \cdot n^{\log_ba}\cdot \log n &\le g(n) \le \frac{c_2}{\log b} n^{\log_ba} \cdot \log n \\\\ \Rightarrow g(n) &= \Theta(n^{\log_ba}\cdot \log n) \\\\ \Rightarrow T(n) &= \Theta(n^{\log_ba}) +\Theta(n^{\log_ba}\cdot \log b) \end{aligned} \end{equation}$$

由于 $\Theta(n^{\log_ba}\cdot \log n)$ 是高阶项，所以

$$T(n) = \Theta(n^{\log_ba}\cdot \log n)$$

1.4.4 主定律应用

$$T(n)=aT(\frac{n}{b})+f(n) = \begin{cases} \Theta(n^{\log_ba}), & \text{if}\quad f(n)=O(n^{\log_ba-\epsilon}) \\\\ \Theta(n^{\log_ba}\cdot \log n), &\text{if}\quad f(n)=\Theta(n^{\log_ba})\\\\ \Theta(f(n)) , & \text{if} \quad f(n) = \Omega(n^{\log_ba+\epsilon}) \end{cases}$$

$T(n)=3T(n/2)+n^2$

1. $a=3, b=2$，$f(n)=n^2$

2. $\log_ba=\log_23 \approx 1.58 < 2$

3. 即 $f(n)<n^{\log_23+\epsilon}$

4. $T(n)=\Theta (f(n))=\Theta(n^2)$

1.4.5 主定律的局限性

主定律在以下情况下不可用：

• $T(n)$ 是非单调函数，比如 $T(n)=\sin(n)$;
• $ f(n)$ 是非多项式，比如 $f(n)=2^n$;
• $a$ 不是常数，比如 $a=2n$；
• $a<1$。

1.5 关于时间复杂度的讨论

1.5.1 渐进分析有什么缺点？

• 由于 渐近分析是假设 $n\to \infty$ 时才成立的，通常情况下 ，算法需要解决的问题规模不会这么大。此时，估算结果会与实际情况有所偏差。
• 由于渐近分析考虑的是时间增长率，忽略掉了低阶项和系数。所以无法区分增长率相同而系数不同的情况。比如 $f(n)=100n$ 和 $g(n)=n\log_2n$ ，按照渐近分析，$f(n)$ 的复杂度要优于 $g(n)$。然而只有当问题规模达到宇宙原子总数量级的时候，这种情况才成立。而我们实际应用中问题规模通常是远小于这个量级。

1.5.2 为什么通常关心的是 $O(f(n))$？

首先， $\Omega(f(n))$ 对各种条件要求比较苛刻，所以我们主要讨论 $\Theta(f(n))$ 和 $O(f(n))$。

• 当我们讨论 “平均” 情况的时候，意味着要对输入数据的分布作出假设。在做这种假设的时候需要大量的数据支持。这就意味着分析结果是不普适的，因为不同的数据有不同的分布。所以通常情况下，“平均” 分析结果并不准确。

• “最坏” 的情况得到的结论容易组合，但“平均”不行，比如：

  1. 算法 1 在最坏的情况下执行 $n$ 次过程 1；
  2. 过程 1 在最坏的情况下执行 $m$ 次过程 2；
  3. 过程 2 执行若干次基本操作。

  此时，我们就可以说算法 1 的最坏复杂程度为 $O(n\times m)$。但是如果算法 1 是在平均情况下执行 $n$ 次过程 1，和 $m$ 次过程 2，我们却不能说算法 1 的复杂度是 $\Theta(n\times m)$。因为过程 1 的数据分布我们不清楚。

1.5.3 如何选择 $O(f(n))，\Theta(f(n))，\Omega(f(n))$？

视情况而定。

• 对实时性要求不高的时候，可以考虑平均复杂度。
• 对实时性要求非常高的情况，就必须考虑最坏的情况了。比如汽车抱死系统，人命关天，时间就是生命。如果用平均复杂度，意味着系统平均反应速度很快，但是偶尔会比较慢。而这个“偶尔”就可能造成无法挽回的损失。

Reference

1. DAS Introduction

2. 算法复杂度分析的那些事, 跟小新一起玩编程

3. Data Structures and Algorithms (DSA)

4. 算法分析中，为什么分析最坏情况而不是平均情况？

5. 关于<<算法导论>>上的主定理（Master Theorem）的证明

6. 主定理的证明及应用举例