预训练语言模型-神经网络语言模型：FFNNLM

1. 简介

统计语言模型中，无论是 n-gram 还是对数线性语言模型都面临一个非常严重的问题——维度爆炸。为了解决维度爆炸问题，Bengio & Bengio 2000 年提出了一种使用分布式词特征表示的方法，也就是后来所说的词向量。

在他们的方法中是将每个词利用神经网络映射到一个连续的向量空间中得到词向量。其实这种方法与对数线性语言模型使用不同特征表示词有异曲同工之妙，只是对数线性语言模型中的特征是人工构建，而且是离散化的。词特征的连续分布式表示相对离散化表示有两个显著的优点：

1. 可以将向量维度压缩到很低；
2. 可以计算词与词之间的距离，用以表示语义相似度。

随着技术的发展，原来的词向量表示维度还是太高。为了降维，人们又发展出了离散化词向量表示技术，但是这种离散化表示技术与对数线性语言模型中的词特征表示法已经不是同一个东西了。

比如，一个 2-d 的向量，离散化向量最多只能表示 4 个词：$[0, 0],[0,1],[1,0],[1,1]$，而连续分布向量则可以表示无数个词：$[0.1,0.2],[0.1, 0.3], [0.11,0.22],…$。所以要想表达更多的词，离散化向量就需要更多的维度，而连续分布向量就不需要。另外，我肯可以看到，离散化向量两两都是正交的，这就意味着两两之间的距离是相等的，也就是丢失了词义。再看连续分布向量，明显两两之间的距离并不相同，这样我们就可以利用这种差异来表示词与词之间的语义相似度。

其实这种将符号用一个连续向量表示的方法在很早之前就出现了，上世纪 80 年代的联结主义就曾使用过。到了 2000 年左右的时候，神经网络技术日渐成熟，人们就利用神经网络将不同的符号表示成连续向量来表示不同的符号之间的关系。

而使用神经网络直接对语言进行建模也是很早就出现了，当时的人们更加关注于每一个词在语言中扮演的角色。利用神经网络对条件概率进行建模的方式首先出现在对词的建模上，即给定前面的字母来预测后一个字母。

最早使用神经网络对语言模型进行条件概率建模的是徐伟，在其 2000 年的论文《Can Artificial Neural Networks Learn Language Models?》提出了一种构建 2-gram 语言模型的方法，但是由于没有隐藏层，且只是二元语言模型，因此限制了其模型泛化能力和上下文语义捕捉能力。

第一个具有现代意义上的真正神经网络语言模型是 Bengio 等人提出的 Feedforward Neural Network Language Model, （FFNNLM）。接下来我们就从这篇文章开始，介绍几个具有代表性的神经网络语言模型。

2. FFNN 语言模型

2.1 神经模型

假设有一个训练集 $X$，训练集中每一句话 $x_i \in X$ 是由词序 $\langle w_1, w_2, …, w_T \rangle$ 组成，其中 $w_t \in \mathcal{V}$，$\mathcal{V}$ 表示词表。词表通常很大，但是是有限的。我们的目标是构建一个模型：

$$f(w_t, ..., w_{t-n+1}) = p(w_t|w_{1:t-1})$$

使得训练集中的句子具有较高的概率分布。另外，模型必须满足一个限制条件：

$$\sum_{i=1}^{|\mathcal{V}|} f(i, w_{t-1}, \cdots,w_{t-n+1})=1$$

有了以上限制条件以后，Bengio 等人就设计出下面一个神经网络模型：

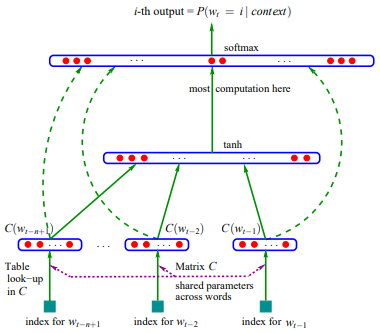
模型可以分成两部分：

1. 一个映射 $C \in \mathbb{R}^{|\mathcal{V}| \times m}$，将词表中的词映射成分布式特征向量，$C(w_i) \in \mathbb{R}^m$。$C$ 是一个自由参数矩阵。
2. 一个概率函数 $g$ 用来计算特征向量序列 $\langle C(w_{t-n+1}), \cdots, C(w_{t-1}) \rangle$ 的条件概率。$g$ 的输出是句子中第 $t$ 个词出现的概率。既然是神经网络语言模型，那么 $g$ 肯定就是一个神经网络啦。

假设有一个句子 $\langle w_1, w_2, …, w_T \rangle$，整个模型的建模过程如下：

1. 选取滑动窗口大小 $n$，对特征向量序列进行滑动切片，得到 $\mathrm{ngrams}=[(w_1, w_2, \cdots,w_n), (w_2, w_3, \cdots, w_{n+1}), (w_3, w_4, \cdots, w_{n+2}),\cdots, (w_{T-n}, \cdots, w_{T})]$。比如 $\langle 我，爱， 北京，天安门 \rangle, n=3$，滑动切片以后得到 $[(我，爱， 北京),(爱，北京，天安门)]$。

2. $\langle w_{t-n+1}, \cdots, w_{t-1} \rangle$ 表示 $\mathrm{ngrams}$ 中第 $t$ 项的前 $n-1$ 个词，比如 $t=1$，则 $\langle w_{t-n+1}, \cdots, w_{t-1} \rangle$ 表示 $(我,爱)$。将其中每个词 $w_i$ 使用 $C$ 映射成特征向量，得到 $\langle C(w_{t-n+1}), \cdots, C(w_{t-1}) \rangle$。比如 $(我，爱，北京)$，$C(我)=[0.1, 0.3, 0.12], C(爱)=[0.2, 0.23, 0.4]$，那么可以得到特征向量序列（其实就是个特征矩阵）：

   $$x_{\mathrm{in}}=\left[ \begin{matrix} 0.1 & 0.2 \\\\ 0.3 & 0.23 \\\\ 0.12 & 0.4 \end{matrix} \right]$$

3. 特征向量序列，就相当于神经网络的输入层。输入层的特征向量序列传递到隐藏层，在隐藏层经过 $\tanh$ 变换：

   $$x_{\mathrm{hidden}} = \tanh(d+Hx_{\mathrm{in}})$$

   其中 $H$ 和 $d$ 分别表示隐藏层的权重和偏置。

4. 经过隐藏层变换之后，传入输出层，在输出层经过线性变换：

   $$x_{\mathrm{out}} = b+Wx_{\mathrm{in}} + Ux_{\mathrm{hidden}}$$

   其中 $b,W,U$ 也是神经网络的参数。经过输出层的变换我们就可以得到一个 $x_{\mathrm{out}} \in \mathbb{R}^{|\mathcal{V}| \times m}$ 的输出矩阵。矩阵的每一列都代表 $w_t$ 可能的分布。

5. 神经网络输出一个 $C(w_t)$ 的候选集，要从这些候选集中选取正确的 $C(w_t)$，就需要将这些候选集转化成概率分布，选择概率最高的那一列对应的向量。最常见的方法是使用 $\mathrm{softmax}$ 函数：

   $$\mathrm{softmax}(x_{\mathrm{out}}) = \frac{\exp(x_{\mathrm{out}})}{\sum_{w_i}\exp(x_{\mathrm{out}})}$$

   这样其实就是对 $(我，爱，北京)$ 的建模过程：输入 $(我，爱)$，输出 $(我，爱)$ 后面所有可能出现的词的概率分布。

有了这样一个过程以后，就可以对整个 $\mathrm{ngrams}$ 进行相同的建模过程。我们的目标是模型每次预测出来的词都是正确的，即我们希望找到一套参数 $\theta$，最大化对数似然函数：

$$L=\frac{1}{T} \sum_t \log f(w_t, _{t-1}, \cdots, w_{t-n+1}; \theta) + R(\theta)$$

其中 $R(\theta)$ 表示正则项（只对权重做正则，不对偏置）。

要找到一套合适的参数，神经网络通常采用的方法是随机梯度下降方法：

$$\theta \leftarrow \theta + \epsilon\frac{\partial \log p(w_t|w_{t-n+1}, \cdots, w_{t-1})}{\partial\theta}$$

其中 $\epsilon$ 表示学习率。

2.2 模型参数量分析

模型参数来源于两部分：

• $C \in \mathbb{R}^{|\mathcal{V}| \times m}$ 是一个矩阵，$C(w_i)$ 表示矩阵第 $i$ 行对应的向量，即为 $w_i$ 对应的特征向量；
• $g$ 是一个神经网络，$\pmb{\omega}$ 表示神经网络的参数，从上面我们可以确定 $\pmb \omega = (b,d,W,U,H)$。

所以，整个模型的参数为 $\theta = (C, b,d,W,U,H)$。

• $C$ 是一个 $\mathbb{R}^{|\mathcal{V}|\times m}$ 的矩阵，所以参数量为：$|\mathcal{V}|\times m$;
• 假设有 $h$ 个神经元，隐藏层的权重 $H$ 参数量为：$h \times (n-1)m$；
• 从隐藏层到输出层的权重 $U$ 参数量为：$|\mathcal{V}| \times h$；
• 从输入层到输出层的权重 $W$ 参数量为：$|\mathcal{V}| \times (n-1)m$；
• 输出层偏置 $b$ 的参数量为：$|\mathcal{V}|$；
• 隐藏层偏置 $d$ 的参数量为：$h$。

那么总的参数量为以上所有参数的数量相加得到：$|\mathcal{V}|(1+mn+h)+h(1+(n-1)m)$。可以看到整个模型的参数随着词表 $\mathcal{V}$ 线性增长，不像统计语言模型那样是指数型增长的。另外，模型参数量也与滑动窗口大小 $n$ 成正比。

3. 实验结果

4. 总结

Bengio 等人提出一种使用神经网络训练 n-gram 模型的方法，该方法具有以下几个优点：

1. 相比传统的统计语言模型，Ngram的N增加只带来线性提升，而非指数复杂的提升；
2. 通过高维空间连续稠密的词向量解决统计语言模型中解决稀疏的问题，不用进行平滑等操作；
3. 另外词向量的引入解决统计语言模型部分相似性的问题，为后续词向量时代的发展做铺垫；
4. 相比传统的统计语言模型，神经网络的非线性能力获得更好的泛化能力，perplexity（困惑度下降）

但是不可避免的也存在一些缺点：

1. 不能处理变长句子序列。由于输入层的神经元是固定的，因此模型必须输入固定长度的序列。
2. 由于输入序列长度是固定的，因此，模型只能对固定长度的上下文进行建模，而不是对整段序列进行建模。
3. 序列中的词没有包含位置信息，而实际上我们知道，对于相同的几个词，放在不同的位置整句话就会表达不同的意思。
4. 尽管全接连神经网络需要学习的参数量远小于 n-gram 但是相比于其他结构的神经网络，其参数量还是过大。

语言模型的发展随着这篇文章的诞生进入了一个崭新的时代。

5. Reference

A Neural Probabilistic Language Model. Yoshua Bengio， Réjean Ducharme，Pascal Vincent，Christian Jauvin，2003