预训练语言模型-统计语言模型平滑技术（补充）

1. N-gram 语言模型

$$p(s) = \prod_{i=1}^n p(w_i|w_1...w_{n-1}) \approx \prod_{i=1}^n p(w_i|w_{i-n+1:i-1})$$

假设我们有一个小数据集：

John read Moby Dick

Mary read a different book

She read a book by Cher

下面我们用 bi-gram 计算 $p(\text{John read a book})$：

$$p(\text{John|<BOS>})=\frac{c(\text{<BOS>, John})}{\sum_w c(\text{<BOS>}, w)} = \frac{1}{3} \\\\ p(\text{read|John})=\frac{c(\text{John, read})}{\sum_w c(\text{John}, w)} = \frac{1}{1} \\\\ p(\text{a|read})=\frac{c(\text{read,a})}{\sum_w c(\text{read}, w)} = \frac{2}{3} \\\\ p(\text{book|a})=\frac{c(\text{a, book})}{\sum_w c(\text{a}, w)} = \frac{1}{2} \\\\ p(\text{<EOS>|book})=\frac{c(\text{book,<EOS>})}{\sum_w c(\text{book}, w)} = \frac{1}{2}$$

所以：

$$\begin{equation} \nonumber \begin{aligned} p(\text{John read a book}) &= p(\text{John|<BOS>})\cdot p(\text{read|John}) \cdot p(\text{a|read}) \cdot p(\text{book|a}) \cdot p(\text{<EOS>|book})\\\\ &= \frac{1}{3} \times 1 \times \frac{2}{3} \times \frac{1}{2} \times \frac{1}{2}\\\\ & \approx 0.06 \end{aligned} \end{equation}$$

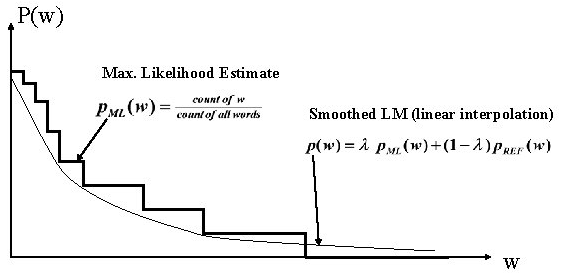
2. Smoothing

现在我们来考虑另外一个句子 $p(\text{Cher read a book})$：

$$p(\text{read|Cher}) = \frac{c(\text{Cher, read})}{\sum_w c(\text{Cher}, w)} = \frac{0}{1}$$

也就是说，最后我们得到的 $p(\text{Cher read a book})=0$，显然这个结果低估了这句话出现的概率，因为仅仅是改了一个名字，这句话仍然是成立的。总不能张三可以读书，李四就不行了吧？

另一个例子 $p(\text{John read one book})$：

$$p(\text{book|one}) = \frac{c(\text{one, book})}{\sum_w c(\text{one}, w)} = \frac{0}{0}$$

这句话甚至会让模型报错。针对以上两种情况，我们必须考虑去解决，而解决的办法就是平滑（Smoothing）。这里我们介绍一些常见的平滑方法。

2.1 Add-1 smoothing（Laplace smoothing）

最简单的方法就是，假设每个二元组（可扩展到 n-gram）比它实际出现的次数多一次，即：

$$p(w_i|w_{i-1}) = \frac{1+c(w_{i-1}, w_i)}{\sum_{w_i}[1+c(w_{i-1}, w_i)]} = \frac{1+c(w_{i-1}, w_i)}{|V|+\sum_{w_i}c(w_{i-1}, w_i)}$$

其中 $|V|$ 表示词表大小。

2.2 Add-k smoothing（Additive Smoothing）

Add-k 平滑假设 n-gram 出现的次数比实际出现的次数多 k 次，通常情况下 $0 \lt k \le 1$：

$$p(w_i|w_{i-n+1:i-1}) = \frac{k+c(w_{i-n+1:i})}{k|V| + \sum_{w_i} c(w_{i-n+1:i})}$$

可以看到 add-1 平滑是 add-k 平滑的一种特殊情况。

2.3 Good-Turing Estimate

假设你在森林探险，一路上遇到了下面这些动物：

10 只野兔，8 只喜鹊，3 头野猪，1 只老虎，1 只狮子，1 匹狼

那么你有多大概率下一次再遇到老虎？显然根据之前的经验是 $1/24$。下一个问题，我们有多大概率下一次遇到的动物是之前没见过的呢，比如大象？如果我们下一次遇到的动物是新的，那么它相当于在我们的样本中出现了一次，要根据现有的经验来估计的话，最接近的应该是用那些现在也只出现了一次的动物的概率来估计才合理，即：

$$p(新动物) = (老虎+狮子+狼)/24=3/24=1/8$$

其实这就是 Good-Turing 平滑的基本思想：

用只出现过一次的事件的总和来估计未出现事件的概率。

在这种情况下，我们回到第一个问题：下一次有多大概率遇到老虎？显然概率应该比 $1/24$ 低了。我们应该怎样来估计具体概率呢？

Good-Turing Estimate 假设对于任意出现了 $c$ 次的 n-gram，我们假设它实际应该出现 $c^*$ 次：

$$c^* = (c+1)\frac{n_{c+1}}{n_c}$$

其中 $n_c$ 表示出现了 $c$ 次的 n-gram 数目，那么该 n-gram 出现的概率为：

$$p(w_{i-n+1:i}) = \frac{c^*}{N}$$

其中 $N=\sum_{c=0}^\infty n_c c^*$。注意：

$$N=\sum_{c=0}^\infty n_c c^* = \sum_{c=0}^\infty(c+1)n_{c+1}=\sum_{c=0}^\infty cn_c$$

所以其实 $N$ 就是 n-gram 总数。所以：

$$p(w_i|w_{i-n+1:i-1}) = \frac{c^*(w_{i-n+1:i})}{\sum_{w_i} c^*(w_{i-n+1:i})}$$

实际上 Good-Turing 假设是可以通过数学推导得到的，具体推导过程见：An empirical study of smoothing techniques for language modeling. page 9。

注意：根据 $c^*$ 公式可知，$n_c$ 不可以等于 0，因此我们需要进一步平滑。关于这一部分可以参考：Gale and Sampson (1995)。

在实际建模过程中，我们很少直接使用 Good-Turing 平滑，但是它是后续很多平滑技术的基础。

2.4 Jelinek-Mercer Smoothing

考虑一种情况：

$$p(\text{the|Burnish})=0, \quad p(\text{aaa|Burnish})=0 \\\\ \Downarrow \\\\ p(\text{the|Burnish})=p(\text{aaa|Burnish})$$

然而，根据我们的直觉，应该是:

$$p(\text{the|Burnish}) \gt p(\text{aaa|Burnish})$$

因为 $\text{the}$ 在英文中太常见了，而 $\text{aaa}$ 是非常罕见的。为了获取这种信息，我们可以将 uni-gram 的信息插入到 bi-gram 中去，这就是所谓的插值法。

$$p_{\text{interp}} = \lambda p(w_i|w_{i-1}) + (1-\lambda)p(w_i)$$

其中 $0 \le \lambda \le 1$。虽然 $p(\text{the|Burnish})=p(\text{aaa|Burnish})$，但是 $p(\text{the}) \gg p(\text{aaa})$，所以

$$p_{\text{interp}}(\text{the|Burnish}) \gg p_{\text{interp}}(\text{aaa|Burnish})$$

通常我们用低阶的 ngram 对高阶的 ngram 进行插值。后来人们又提出一个变种：

$$p_{\text{inter}}(w_i|w_{i-n+1:i-1}) = \lambda_{w_{i-n+1:i-1}} p(w_i|w_{i-n+1:i-1}) + (1-\lambda_{w_{i-n+1:i-1}})p_{\text{inter}}(w_i|w_{i-n+2:i-1})$$

看起来比较复杂，实际上很简单。举个例子 3-gram “（我，是， 谁）”，那么 $p(谁|我,是)$ 变成：

$$p_\text{inter}(谁|我,是) = \lambda_1 p(谁|我,是) + (1-\lambda_2) p(谁|是) + (1-\lambda_3) p(谁)$$

甚至我们可以将 0 阶项 $\frac{1}{|V|}$ 也加进去。现在的问题就是如何确定 $\lambda$ 的值了。这里用到的就会 Baum-Welch 算法，也就是 HMM 模型的参数估计算法，在这里不展开讲后面介绍 HMM 的时候详细介绍。

2.5 Katz Smoothing

Katz 平滑是通过将高阶 ngram 与低阶 ngram结合的方法扩展了 Good-Turing 平滑。我们先考虑 bi-gram 的情况，$n=c(w_{i-1:i})$ 表示二元组出现的次数，我们用下面的方法就算修正后的次数：

$$\alpha_\text{katz}(w_{i-1:i}) = \cases{ d_nn & if n > 0\\\\ \alpha(w_{i-1}) p(w_i) & if n=0 }$$

所有非零的二元组出现的次数都以 $d_n=\frac{n^*}{n}$ 为系数打了折扣，将非零的二元组频次扣掉的部分根据低阶项分配给零频次的二元组，其中：

$$\begin{equation} \nonumber \begin{aligned} \alpha(w_{i-1}) &= \frac{1-\sum_{w_i:c(w_{i-1:i})>0}p_\text{katz}(w_i|w_{i-1})}{\sum_{w_i:c(w_{i-1:i})=0}p(w_i)}\\\\ &= \frac{1-\sum_{w_i:c(w_{i-1:i})>0}p_\text{katz}(w_i|w_{i-1})}{1-\sum_{w_i:c(w_{i-1:i})>0}p(w_i)} \end{aligned} \end{equation}$$

我们通过下式计算 $p_\text{katz}(w_i|w_{i-1})$:

$$p_\text{katz}(w_i|w_{i-1}) = \frac{\alpha_\text{katz}(w_{i-1:i})}{\sum_{w_i}\alpha_\text{katz}(w_{i-1:i})}$$

在 Katz 平滑中认为高频出现的 ngram 出现的次数是可靠的，因此对于大于一定次数的 ngram 不进行折扣，即当 $n>k$ 时，$d_n=1$，通常令 $k=5$。对于 $n<k$ 的 ngram 则采取折扣的方法：

• 让折扣去掉的量成正比

  $$1-d_n = \mu(1-\frac{n^*}{n})$$

• 让打折去掉的量（也就是摊到没出现过的 ngram 上的量）与 Good-Turing 摊到没出现过的 gram 上的量相等。Good-Turing 中 $n_0\times(0+1)\frac{n_1}{n_0}=n_1$，Katz 的折扣量为 $\sum_{n=1}^kn_c(1-d_n)d$。于是：

  $$\sum_{n=1}^kn_c(1-d_n)d = n_1$$

  由此可得

  $$d_n = \frac{\frac{n^*}{n}-\frac{(k+1)n_{k+1}}{n_1}}{1-\frac{(k+1)n_{k+1}}{n_1}}$$

2.6 Witten-Bell Smoothing

WB 平滑可以看成是 Jelinek-Mercer 平滑的一种特殊情况：将 $\lambda_{w_{i-n+1:i-1}}$ 看成是取高阶 ngram 的概率，则 $1-\lambda_{w_{i-n+1:i-1}}$ 可看成是取低阶 ngram 的概率。WB 的基本思想是这样的：

• 如果训练集中出现了高阶 ngram，那么我们应该采用高阶 ngram 来建模；
• 如果训练集中没有出现高级 ngram，那我们就退而求其次用 低阶 ngram 来建模。

我们可以把 $1-\lambda_{w_{i-n+1:i-1}}$ 理解成，当出现了 $w_{i-n+1:i-1}$ 的 ngram 后，没有出现在其后的词的概率。有点绕，举个例子说明：

$w_{i-n+1:i-1}=(我,爱)$ 出现在训练集中，但是 $(我,爱,哈)$ 在训练集中没有，那么 $1-\lambda_{w_{i-n+1:i-1}}$ 就表示 $(我,爱,哈)$ 的概率。

其实很容易理解，某个词要么出现在某 (n-1)gram 后面，要么不出现在其后面，总的概率就是两种情况相加。

$$1-\lambda_{w_{i-n+1:i-1}} = \frac{N_{1+}(w_{i-n+1:i-1} \odot)}{N_{1+}(w_{i-n+1:i-1} \odot) + \sum_{w_i}c(w_{i-n+1:i})}$$

其中 $N_{1+}(w_{i-n+1:i-1} \odot)=|{w_i:c(w_{i-n+1:i-1}, w_i)}>0|$ 表示 $w_{i-n+1:i-1}$ 历史 (n-1)gram 后面出现次数不为 0 的词的个数。

$$p_\text{WB} = \frac{c(w_{i-n+1:i})+N_{1+}(w_{i-n+1:i-1} \odot) p_\text{WB}(w_i|w_{i-n+2:i-1})}{\sum_{w_i} c(w_{i-n+1:i}) + N_{1+}(w_{i-n+1:i-1} \odot)}$$

2.7 Absolute Discounting

JM 平滑是按比例扣除部分概率，而 AD 则是扣除固定的概率：

$$p_\text{AD}(w_i|w_{i-n+1:i-1}) = \frac{\max(c(w_{i-n+1:i})-D, 0)}{\sum_{w_i}c(w_{i-n+1:i})} + (1-\lambda_{i-n+1:i-1})p_\text{AD}(w_i|w_{i-n+2:i-1})$$

为了使概率和为 1，令：

$$1-\lambda_{i-n+1:i-1}=\frac{D}{\sum_{w_i} c(w_{i-n+1:i})}N_{1+}(w_{i-n+1:i-1} \odot)$$

通常令

$$D = \frac{n_1}{n_1+2n_2}$$

其中 $n_1, n_2$ 分别表示出现了 1 次和 2 词的 ngram 数量。

2.8 Kneser-Ney Smoothing

KN 平滑是 AD 的一种改进。比如，英文中 San Francisco 这个组合很常见，从而使得 Francisco 这个 unigram 概率比较高，但是实际上 Francisco 往往只和 San 搭配，出现在 San 后面。而如果用 Absolute，如果没见过 Francisco（ 不是 San） 这样的组合时，回退到 Francisco 的 unigram 概率，这使得 * Francisco 的概率也挺大，但实际上这是不正确的。所以我们应该给 Francisco 一个比较合理的 unigram 概率。

基本的思想就是：

unigram 的概率不仅仅依赖于它的频率，还应该考虑到它出现在多少个上下文中。

$N_{+1}(\odot w)$ 表示 $w$ 出现过的上下文的个数，$N_{+1}(\odot \odot) = \sum_{w’}N_{+1}(\odot w’)$。

KN 平滑就是在 AD 的基础上，令 $p(w_i)=N_{+1}(\odot w_i)/N_{+1}(\odot \odot)$。

总结

Reference

An empirical study of smoothing techniques for language modeling. Stanley F.Chen, Joshua Goodman. 1999