过拟合(overfitting)
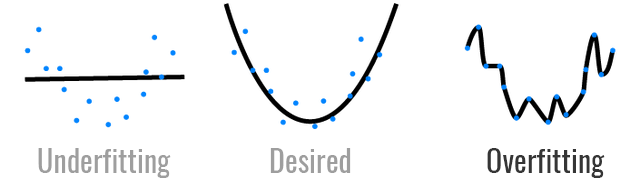
我们在训练机器学习/深度学习模型的时候,通常会发现,模型在训练数据集上表现非常好,但是在验证集上却非常差,这种现象就是过拟合。我们训练模型的目的不是希望它在训练集上有良好的表现,而是希望在验证集(更准确的说是在实际数据,验证集可以认为是用于模拟真实数据的数据集)上有好的表现。所以过拟合的模型非我所欲也。
从上面的图中,我们可以直观的看出来,从左至右模型的复杂度越来越高。所以通常造成模型过拟合的原因就是模型复杂度过高,对数据过于敏感(模型稳定性差)。
这里稍微解释一下,为什么模型复杂度高或者模型不稳定就会造成模型过拟合?
模型复杂度过高
根据泰勒定理,在一个区间之内我们可以通过泰勒展开式来逼近任意可导函数:
当泰勒展开式的逼近项阶数越高,则越接近原始的函数,但泰勒展开式的表达形式也越复杂:
- 当 $n=0$ 时,$f(x)=f(a)$;
- 当 $n =1$ 时,$f(x)=f(a)+w_1\cdot (x-a)$;
- 当 $n=2$ 时,$f(x)=f(a)+w_1\cdot (x-a)+w_2\cdot (x-a)^2$
- $\cdots$
这是一目了然的。虽然神经网络不是通过泰勒展开式进行逼近,但是其遵循的规律是相同的,即越是逼近原始函数就需要更复杂的逼近函数。
如果原始函数是训练数据分布,机器学习/深度学习模型表示逼近函数。那么如果模型出现过拟合现象,一定是一个复杂度过高的模型。
模型不稳定
稳定性代表在小的扰动下,其轨迹不会有太大的变化。放在模型训练过程,我们可以从两个方面理解这句话:
- 训练样本中的异常值对模型不会产生太大的影响;
- 相对大量的训练样本,小部分样本不会对模型产生太大影响。
对于一个不够稳定的模型,遇到任意的样本点都会对模型产生较大的影响,使模型也要去拟合那些异常点和小样本点,就会形成上图右侧的复杂曲线。
训练过度,训练数据不足等也是造成过拟合的重要原因,但是这些都是外因,这里我们只讨论模型本身的原因。
L1正则化
首先考虑模型复杂度过高带来的过拟合问题。我们先定义模型复杂度,假设神经网络 $l$ 层的输出为:
在机器学习/深度学习中,$x_i$ 通常表示特征项,$w_i$ 表示对应特征在任务中所起到的作用。过拟合是因为我们采用了过多无用特征,比如一个成年人,通过(身高,体重,头发长度)等几个特征就可以大致判断其性别,但是如果还有其他额外特征(是否戴眼镜,学历,肤色)等等没这些特征很有可能对我们造成干扰,从而造成误判。从这个例子中我们可以看出,是由于无用特征过多造成的过拟合,那么我们可以定义模型复杂度:
$f(X)=b + w_1x_1 + w_2x_2+\cdots+w_nx_n$ 中 $n$ 表示模型的复杂度
在实际中,我们无法得知那些特征是有效的,那些是多余。所以直接从特征着手去解决是比较困难的。那么我们只能从权重 $(w_1, w_2, …, w_n)$ 角度考虑,如果我们能令无用特征的权重为 0 就等效于去除无效特征,降低模型复杂度,从而解决过拟合问题。
从这个角度出发,我们可以在损失函数中引入 L1 正则项:
下面我们看,为什么在原有的损失函数上加上 L1 正则化项之后就能将权重拉向 0?
我们举一个最简单的例子,假设我们有一组数据 $[(x_1, y_1), (x_2, y_2), …, (x_n, y_n)]$,我们的模型为 $y=w\cdot x$ ,只有一个参数 $w$。我们从训练样本中随机抽取数据,使用 MSE 损失函数对模型进行训练,最后在 $w=0.5$ 时,$loss=0$。

|

|
现在我们单独把 L1 正则项的图像画出来:

当 $w=0$ 时,$L_1=0$。现在我们把 MSE 损失项和 L1 项叠加在一起:
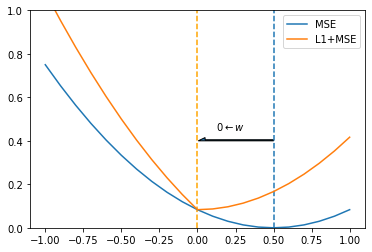
从图中我们可以很清楚的看到, 加入 L1 正则项的损失函数最小值在 $w=0$ 处。也就是说,在训练过程中权重的更新方向是向 0 靠近的。这样模型在训练过程中可以将无用的特征权重置零,达到减小模型复杂度的目的,从而解决(严格意义上来说是缓解)过拟合的问题。
L2 正则化
现在我们来考虑模型不稳定带来的过拟合问题。不稳定的模型本质上是输出相对输入变化率太大,仍然以 $y=w \cdot x$ 为例,$y+\Delta y = w \cdot (x+\Delta x)$,当模型不稳定的时候,一个很小的 $\Delta x$ 就可能带来一个很大的 $\Delta y$。这种相对变化率的评估指标就是导数:
也就是当权重较低的时候,模型更加稳定。所以为了使模型更加稳定,我们需对权重设定一个上限,超过这个上限我们就认为模型有较大的过拟合风险,即我们令 $w_1+w_2+ \cdots w_n < \tau$。
我们当然可以在训练过程中,每一次权重调整都去验证看看权重是否符合这个限定条件。但是这种方法显然比较麻烦,而且比较消耗算力。我们希望将这种限制直接添加到损失函数,使得每一次权重更新都自动满足这个限定条件。相当于我们要对有限制条件的微分方程求解,很自然地我们会引入拉格朗日乘子法。
L2 正则化就是假设限制条件是 $\lambda ||w||_2^2$,其中 $||w||_2^2$ 表示:
此时经过 L2 正则化后的损失函数为:
关于拉格朗日乘子可以参考这篇文章:An Introduction to Lagrange Multipliers。
下面我们来看,为什么 L2 正则化可以起作用?
仍然以 $y = w \cdot x$ 为例,我们将 MSE 与 L2 项叠加在一起的图像画出来:
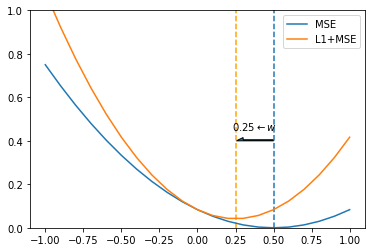
从上图我们可以很清晰的看出,L2 正则项确实可以将权重拉向小量,但是不会到 0。
$\lambda$ 的影响
不同的 $\lambda$ 对损失有什么影响呢?

如果 $\lambda=0$ ,相当于沒有做正则化,模型就会过拟合 。 当 $\lambda$ 一直变大,模型就 overfitting → generalization → underfitting。
L1 VS. L2
- L1 正则项使权重稀疏,因为有些权重会置零。L2 正则项使权重平滑,增加模型稳定性。
- L1 正则不容易求导,计算量大。L2 正则容易求导。
- L1 正则项对异常值更鲁棒
什么时候用L1/L2?
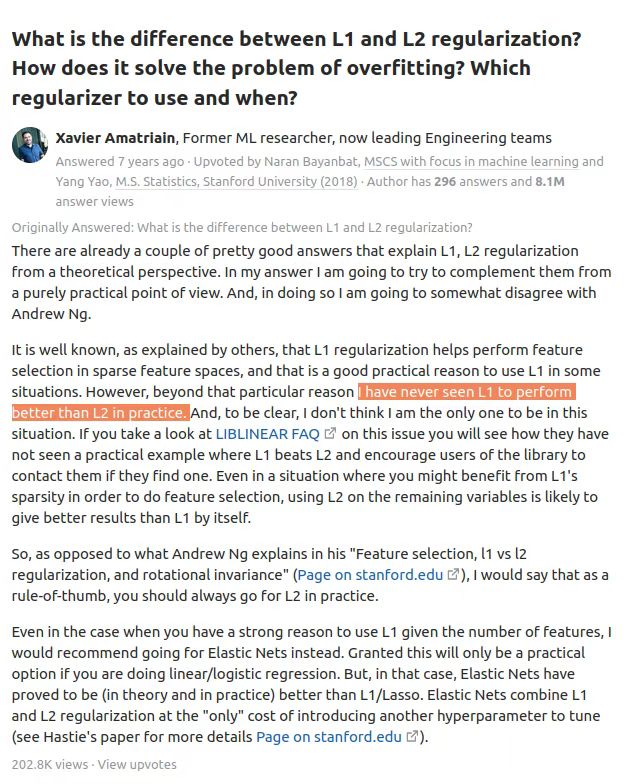
在实际的应用中,L2 正则几乎总能取得比 L1 更好的效果。
其他的正则化方法
Elastic net
Entropy Regularization
Label smoothing
其中 $k$ 表示类别数目。
Dropout
随机“切断”一部分神经元的连接。
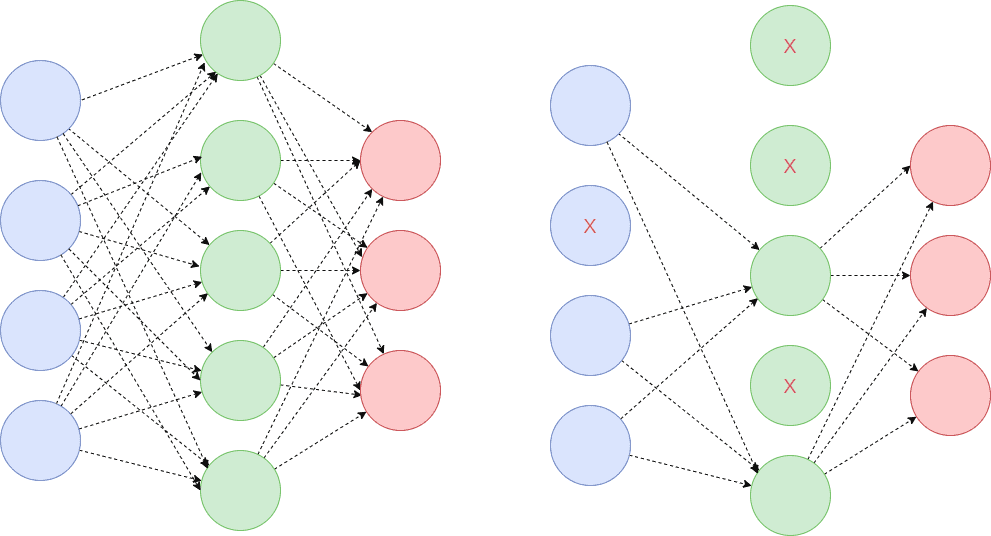
Inverted dropout:为了避免激活函数的输出过大,模型以 $1-p$ 的概率对激活函数进行缩放。
Gaussian dropout:不再“切断”神经元,而是在神经元中添加噪声:
- 减少测试期间的计算量;
- 无需对权重进行缩放;
- 训练速度更快。
DropConnect:将神经元的权重随机置零:
其中,$r$ 表示网络层输出,$v$ 表示输入,$W$ 表示权重,$M$ 表示二元矩阵。
Variational Dropout:每一个训练步都是用相同的 dropout 掩码矩阵,通常用于RNN。
Attention Dropout:以 $p$ 概率随机 drop 掉注意力值。
Adaptive Dropout:不同单元的神经元有不同的 drop 概率。
Embedding Dropout:在嵌入矩阵中进行 drop。
DropBlock:在一个连续区域内,drop 掉所有的单元,通常用于 CNN。
Stochastic Depth
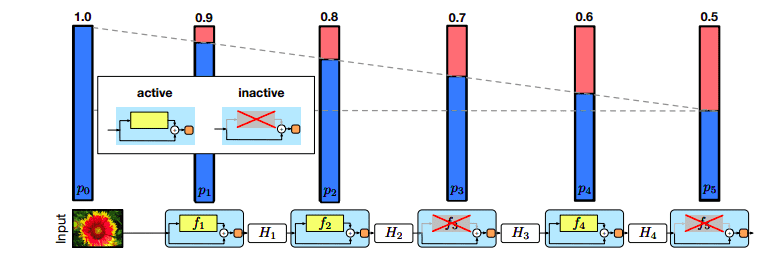
随机 drop 掉一些网络层。
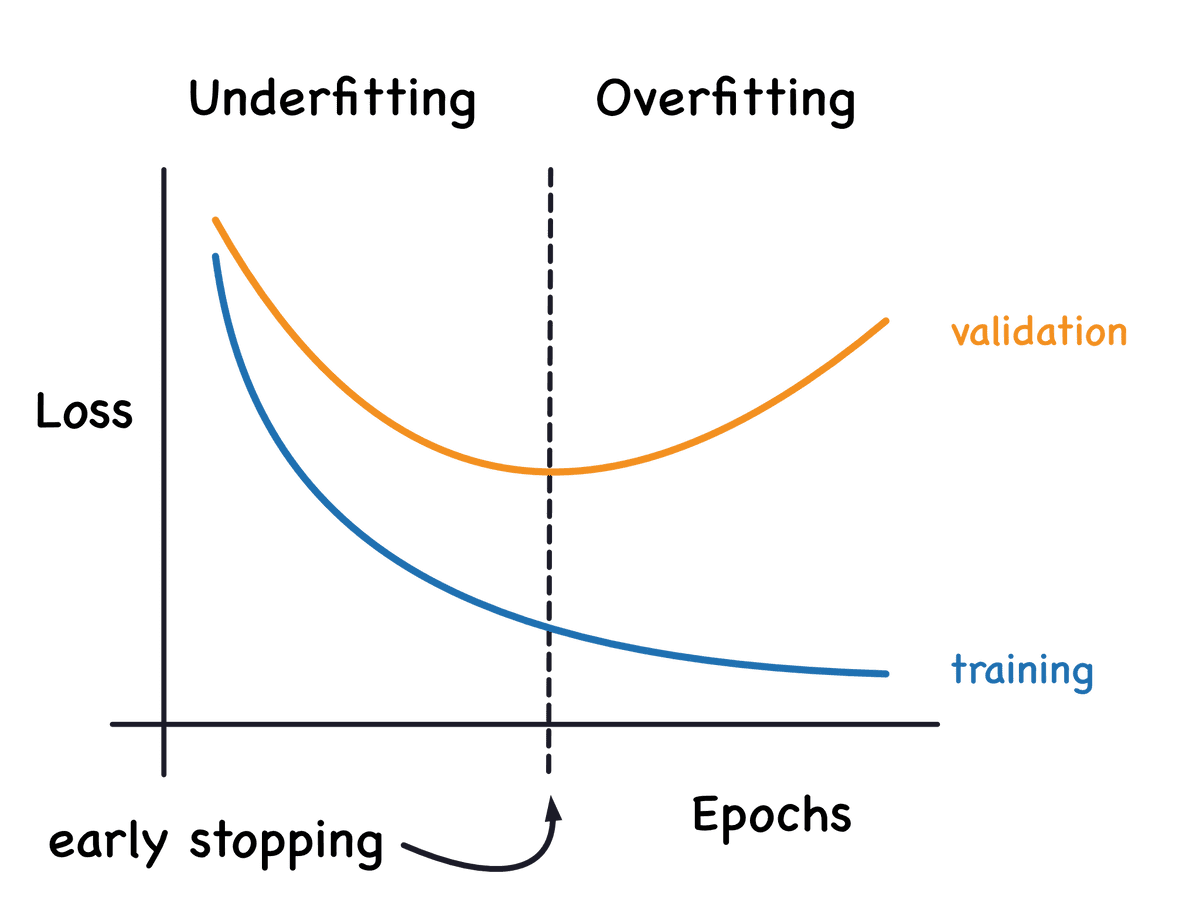
Early stopping
Parameter sharing
不再在权重上施加惩罚项,而是强行令一部分权重相等,通常用于 CNN。
Batch normalization
Data augmentation
- Basic Data Manipulations:图像剪切,旋转,翻转等。
- Feature Space Augmentation:比如使用自编码器提取图像隐特征。
- GAN-based Augmentation:基于生成对抗网络生成数据。
- Meta-Learning:给 GAN 随机喂一张图片,然后将生成的图片和原始图片同时喂给第二个网络,然后让第二个网络对比两张图片,然后告诉我们哪张图片更好。



