Rogerspy's Home

Levenshtein Transformer 不仅具有序列生成的能力，还具有了序列修改的能力。然而我们会发现，整个模型实际上是很复杂的。从模型结构上讲，除了基础的 Transformer 结构，还额外增加了三个分类器：删除分类器、占位符分类器和插入分类器。从训练过程来讲，LevT 需要一个参考策略（expert policy），这个参考策略需要用到动态规划来最小化编辑距离。这样无论从训练还是才能够推理角度，我们都很难保证模型的效率。那么有没有一个既有 LevT 这样的强大的能力，又保持高效简洁的模型呢？Insertion-Deletion Transformer 就这样应运而生了（内心 os：你永远可以相信宋义进:joy:）。

1. Abstract Framework

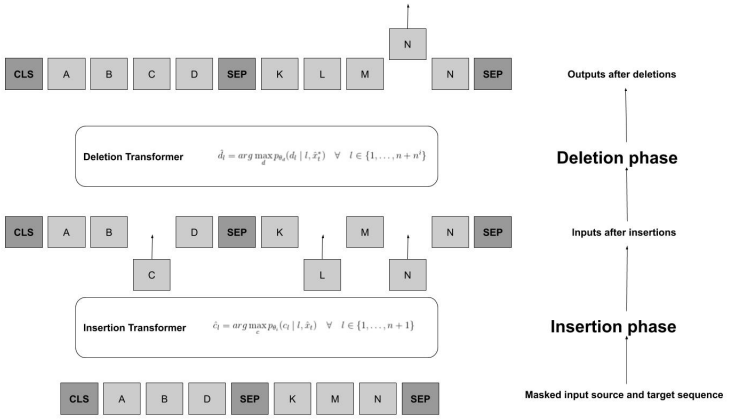
Insertion-Deletion Transformer 实际上是 KERMIT 的扩展版，之前我们介绍过 KERMIT 是 Insertion Transformer 的泛化版，这里再次对模型进行进化。

Insertion-Deletion Transformer 只包含两个步骤：插入和删除。其中插入操作和 KERMIT 是一样的，之后将插入生成的序列传递给删除模块，进行删除操作。

  • $\vec{y}_t$ —— 表示 $t$ 时刻的目标序列；
  • $c \in C$ —— $C$ 表示词表；

  • $p(c, l|\hat{y}_t)$ —— 表示在 $l \in \{1, …, |\vec{y}_t|\}$ 每个位置上插入 $c$ 的概率分布；

  • $d \in [0, 1]$ —— 表示删除操作的概率，$d=0$ 表示不删除， $d=1$ 表示删除；

  • $p(d,l|\vec{y}_t)$ —— 表示 $l \in [0, |\vec{y}_t|]$ 每个位置上的元素的删除操作的概率分布。

1.1 Training

  1. 采样生成步骤 $i \sim \mathrm{Uniform([1, n])}$;
  2. 采样前 $i-1$ 次插入操作的排列组合 $z_{1:i-1} \sim p(z_{1:i-1})$；
  3. 将序列传入插入模型，按照 $p(c_i^z|x_{1:i-1}^{z, i-1})$ 概率分布进行插入操作（后续 $x_{1:i-1}^{z, i-1} $ 简写成 $\hat{x}_t$）；
  4. 将上面经过插入操作后的序列传入删除模型；
  5. 删除模型按照 $p(d_l| l, \hat{x}_t^\star)$ 的删除概率分布进行元素删除，然后将删除操作后的序列输出。

实际上前面三步和 KERMIT 的过程是一致的。

1.2 Learning

模型整体是将两个 Transformer 的解码器堆叠在一起，一个作为插入模型，另一个作为删除模型，同时训练各自的参数 $\theta_i$ 和 $\theta_d$。删除模型的信息依赖于插入模型的当前状态。我们的目标是通过并行解码最大化下式：

需要注意的是，在计算梯度的时候，两个模型是分开的，也就是说删除模型的梯度没有传递给插入模型。这个其实也好理解，举个例子：

目标序列是 $[A, B, C, D, E, F, G]$，解码的顺序是：

  1. $[]$；
  2. $[D]$；
  3. $[B, D, F]$；
  4. $[A, B, C, D, E, F, G]$。

假设现在 $t=3$，$\vec{y}_t=[B, D, F]$，这就是此时插入模型和删除模型的 target。由于并行解码用到的是平衡二叉树，那么每个时刻的 target 是固定的，我们就可以用这个 target 计算损失，然后计算删除模型和插入模型的各自梯度。

由于删除模型的信息依赖于插入模型，那么久有可能删除模型学习不到任何东西，即没有可删除的信息。有两方面原因会造成这个结果：

  1. 插入模型太好了，删除模型没有什么好删除的，这样删除模型没有损失，也就没有梯度，也就不能更新权重，造成什么也没学到；
  2. 插入模型什么也没插入，那么删除模型也就没有什么可删除的，也会造成什么也学不到。

为了解决这个问题，作者提出以 $p_{\mathrm{adv}}$ 的概率 mask 掉目标序列中的一部分元素，这样会使插入模型错误率上升，这样删除模型就能学到新的权重了。

2. Experiments

作者在这里没有做机器翻译的相关实验，而是做了另外两个实验：

  • Learning shifted alphabetic sequences
Alphabetic Sequence Shifting BLEU
Insertion Model (KERMIT) 70.15
Insertion Deletion Model 91.49
  • Learning Caesar’s Cipher
Caesar’s Cipher BLEU
Insertion Model (KERMIT) 35.55
Insertion Deletion Model 37.57

这篇文章很短，所以有些细节可能没有讲的很清楚，期待作者放出源码，到时候跟着源码再看一遍，应该会有新的收获。另外，由于作者这里没有放出机器翻译相关的实验，所以还不太清楚其在机翻上的表现，但是个人比较期待。

Reference

Insertion-Deletion Transformer, Laura Ruis, Mitchell Stern, Julia Proskurnia & William Chan. 2020. arXiv: 2001.05540

 上一页

Transformer parallel-recurrent

 评论