
之前我们介绍了几个 Insertion-based 的序列生成的方法,使我们跳出传统的从左到右的生成顺序的思维定式。既然有 Insertion 操作,那么一个很自然的想法就是,我们能不能再加入一个 deletion 操作呢?这样我们不仅能生成序列,还可以修改生成的序列,岂不美哉?Gu et al. (2019) 就针对这种想法提出了 Levenshtein Transformer 的模型。Levenshtein Distance 我们不陌生,也就是编辑距离,这里面涉及到三种操作:insertion、deletion、replace,严格意义上来讲 replace 实际上就是 insertion 和 deletion 的组合,所以 LevT 模型只用到了插入和删除操作。
1. Abstract Framework
LevT 不同于一般的生成模型,它不仅可以生成序列,还可以修改序列。这样的话他应该算是 generation model 和 refinement model 的组合体,比如,如果 解码端初始化是一个序列,那么该模型就是普通的生成模型;而如果解码端初始化是一段低质量的序列,那么该模型可以通过插入和删除操作将输入序列修改成一段高质量的序列,比如翻译后编辑任务(translation post-editing)。
作者将 generation 和 refinement 两个任务当成一个马尔科夫决策过程(Markov Decision Process, MDP),使用一个五元组来表示:$(\mathcal{Y, A, E, R}, y_0)$。
- $\mathcal{Y=V}^{N_{\max}}$ —— 表示一个序列集合,其中 $\mathcal{V}$ 表示词表;
- $\pmb{a} \in \mathcal{A}$ —— 表示一个行为,$\mathcal{A}$ 表示动作集合;
- $\pmb{r} \in \mathcal{R}$ —— 表示回馈,$\mathcal{R}$ 表示回馈函数;
- $\mathcal{E}$ —— 表示一个主体(agent);
- $\pmb{y}_0$ —— 表示初始序列,要么为空,要么是由其他模型生成的序列。
马尔科夫决策过程如下:一个主体 $\mathcal{E}$ 接受一个行为 $\pmb{a}$,得到一个序列 $\pmb{y}$, 然后反馈函数 $\mathcal{R}$ 度量这个序列与真实的序列的误差:$\mathcal{R(y)=-D(y, y^{\star})}$。由于操作基于插入和删除,自然地,我们可以使用 Levenshtein Distance 去度量。主体要采取什么动作则由策略 $\pi$ 决定:将目前的序列映射成行为概率分布,即 $\pi: \mathcal{Y \rightarrow P(A)}$。
LevT 的任务就是给定一个序列 $\pmb{y}^k = ( y_1, y_2, …, y_n)$,生成 $\pmb{y}^{k+1} = \mathcal{E(\pmb{y}^k, \pmb{a}^{k+1})}$,其中 $y_1$ 和 $y_n$ 分别为 $< s >$ 和 $< /s >$。
注意:在下面的描述中上角标 $k, k+1$ 省略,以及对于条件概率生成,比如机器翻译,源序列输入 $x$ 在下面的公式中也省略了。
删除
删除策略是一个 $n$ 重伯努利分布:输入一个序列 $y$,对于序列中的每一个元素 $y_i \in \pmb{y}$ 要么保留,要么删除,即 $d = 1(删除)$ 或者 $d = 0 (保留)$。为了避免 $< s >$ 和 $< /s >$ 被删除,这里强制令 $\pi^{\mathrm{del}}(0|0, \pmb{y}) = \pi^{\mathrm{del}}(0|n, \pmb{y}) = 1$。
插入
相对删除操作,插入就比较复杂了,因为你进要预测插入的词,还要预测插入的位置,我们还希望在同一个位置尽可能多的插入更多的词,这样就相当于模型具有并行的能力。这里作者将插入位置的预测称之为占位符预测(placeholder prediction);将词的预测称之为词预测(token prediction)。
第一步:占位符预测
$(y_i, y_{i+1})$ 表示接下来的词插入到 $y_i, y_{i+1}$ 之间。注意这里可以预测多个插入位置。
第二步:词预测
每个位置可以有多个词。
这两个步骤可以看成是 Insertion Transformer 和 masked language model 的混合体。
删除和插入的综合
最后,作者将序列的生成分成三个阶段:① 删除词;② 插入占位符;③ 用词替换占位符。其中每一步都是可以并行处理的。
给定序列 $\pmb{y}=(y_0, …, y_n)$,预测行为 $a = \{\underbrace{d_0, …, d_n}_{删除操作}; \underbrace{p_0,…,p_{n-1}}_{占位符预测}; \underbrace{t_0^1,…,t_0^{p_0},…,t_{n-1}^{p_{n-1}}}_{词预测}\}$:
其中 $\pmb{y’}=\mathcal{E}(\pmb{y}, \pmb{d})$,$\pmb{y’’}=\mathcal{E}(\pmb{y’}, \pmb{p})$。
2. Levenshtein Transformer
2.1 Model
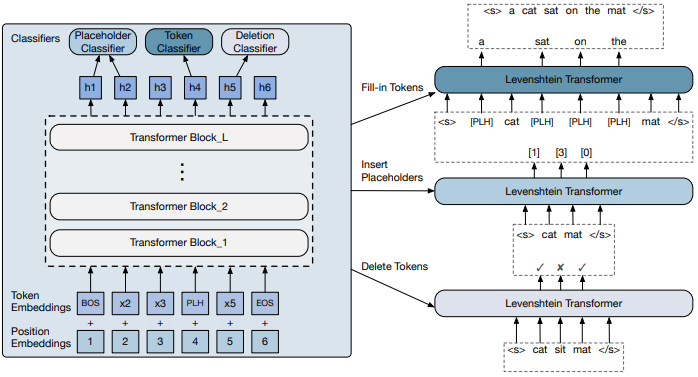
模型的整体结构仍然采用 Transformer,第 $l$ 个注意力层的状态如下:
其中 $E \in \mathbb{R}^{\mathcal{|V|}\times d_{model}}$ 表示词向量,$P \in \mathbb{R}^{N_\max \times N_\max}$ 表示位置向量。
从图中我们可以看到,解码器的输出 $(\pmb{h}_0,…,\pmb{h}_n)$ 被传入到三个分类器中:删除分类器、占位符分类器和词分类器。
删除分类器
其中 $A \in \mathbb{R}^{2 \times d_{model}}$。对序列中除了 $< s >$ 和 $< /s >$ 之外的所有元素进行分类。
占位符分类器
其中 $B \in \mathbb{R}^{(K_\max+1)\times (2d_{model})}$,$(0 \sim K_\max)$ 表示在当前位置上插入占位符的个数,本文中占位符用
[PLH]表示。比如 $(A, D) \rightarrow (A, [\mathrm{PLH}], [\mathrm{PLH}], D)$。词分类器
其中 $C \in \mathbb{R}^{\mathcal{|V|}\times d_{model}}$。
2.2 Dual-policy Learning
接下来一个关键的问题是,模型怎么学习?最简单的,我们可以用模仿学习。

假设我们现在有一个参考策略 $\pi^{\star}$,这个参考策略要么使用真值,要么可以加入少许噪声。我们的目标是最大化以下期望值:
其中 $\pmb{y’}_\mathrm{ins}$ 表示在 $\pmb{y}$ 上插入占位符以后的序列。$\tilde{\pi}_\mathrm{del}, \tilde{\pi}_\mathrm{ins}$ 是输入策略,我们不断从由它们导致的状态分布中抽样分布(序列),这些状态首先由参考策略运行,然后返回其行为,我们就是要去最大化这些行为概率。我们有两种方法定义输入策略:① 在真值上加噪; ② 使用对抗策略。如下图所示:
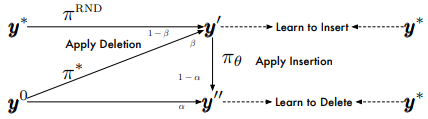
删除操作,我们可以定义:
其中 $\pmb{y}^0$ 是初始输入,$\alpha \in [0, 1]$ 表示我们交替从 $\pmb{y}^0$ 和 $\pmb{y’}$ 中选取样本,$u \sim U[0,1]$,$\pmb{y’}$ 是任意准备插入的序列,$\pmb{p}^\star$ 取自参考策略, $\tilde{\pmb{t}}$ 取自当前策略。用这种方法,我们既可以学习对初始序列 $\pmb{y}_0 $ 如何删除,也可以学习在整个过程中如何对序列删除。
插入操作,类似于删除操作:
这里 $u \sim U[0,1]$,$\beta \in [0, 1]$,$\pi^{\mathrm{RND}}$ 是从真值序列中随机丢弃一个字符。
现在还剩最后一个问题:如何构建参考策略?
Oracle:
其中 $\mathcal{D}$ 表示 Levenshtein distance。
Distillation:我们首先训练一个 AR 模型,然后把真值序列 $\pmb{y}^\star$ 用 distillation 模型的 beam search 结果 $\pmb{y}^{AR}$ 进行替换。实验结果表明这个方法是对上一个方法的大幅改进,既可以边生成边修改,又可以并行。
2.3 Inference

在进行推理的时候采用 贪婪解码。解码终止条件有两个:
- Looping:当两次连续的修改操作(插入和删除)返回相同的序列。可能有两个原因:① 没有可插入或者可删除的词了;② 插入和删除相互抵消了,解码过程陷入死循环。
- Timeout:通过设置最大迭代次数保证模型不会在一个较差的结果上耗费过多时间。
另外为了防止不合理的空占位符的出现,作者这里和 Insertion Transformer 一样采取了惩罚措施:从占位符分类器的输出结果中剪掉 $\gamma \in [0,3]$ 项。
3. Experiments
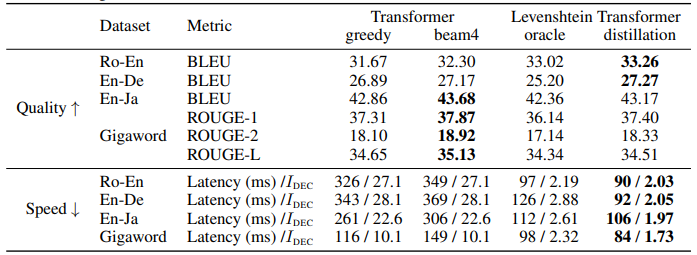
可以看到,Levenshtein oracle 的效果堪比 Transformer,而加了Transformer distillation之后表现几乎总好于 Transformer,并且还快得多。
另外,由于 LevT 还可以进行 refinement, 因此作者还评估了模型的修改效果,下表 APE(automatic post-editing)) 是实验结果:
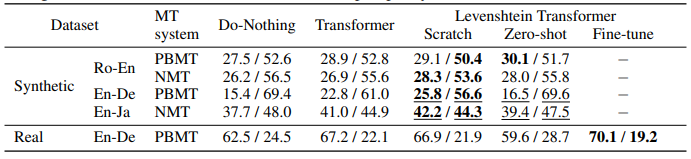
左边的结果是 BLEU 值,右边的结果是 TER 翻译错误率。可以看到,LevT 几乎承包了所有任务上的最优结果,表明了这种修改的可行性。
Reference
- Levenshtein Transformer, Jiatao Gu , Changhan Wang & Jake Zhao (Junbo). 2019. arXiv: 1905.11006
- 香侬读 | 按什么套路生成?基于插入和删除的序列生成方法, 香侬科技, 知乎



