
之前我们介绍的 insertion-based 生成模型实际上都是人为预先定义了生成顺序或者策略,那么我们能不能让模型自己决定要以怎样的顺序生成呢?这就是本文将要讨论的一种解决方案:Insertion-based Decoding with automatically Inferred Generation Order,将序列的生成顺序当成一种隐变量,让模型在预测下一个词的时候自动推理这个词应该所处的位置。
1. Abstract Framework
- $y=(y_1, …, y_T)$ —— 表示待生成的序列;
- $x=(x_1, …, x_{T’})$ —— 表示输入序列;
- $\pi=(z_2, …,z_T,z_{T+1}) \in \mathcal{P}_T$ —— 表示 $y$ 生成的顺序,其中 $\mathcal{P}_T$ 表示 $(1, …, T)$ 的排列组合;
- $y_{\pi} = \{(y_2,z_2),…,(y_{T+1}, z_{T+1})\}$ ——每一步生成的词及其位置。
与一般的标记不同,这里我们分别令 $(y_0, z_0) = (< s >, 0), (y_1, z_1) = (< /s >, T+1)$,表示序列的开始和结尾。
将生成顺序看作隐变量 $\pi$ ,那么对于一个输出句子 $y$ ,取所有顺序的概率之和,作为输出 $y$ 的概率:
其中每个生成顺序的概率为:
其中 $y_{T+2}=< eod >$ 表示结束解码的标志,用 $p(y_{T+2}|\cdot)$ 表示其概率分布。
另外 $z$ 表示生成的单词在句子中的绝对位置。但是这就会有一个问题:我们连最后生成的句序列长度都还不知道怎么能确定当前生成的词在最终序列的绝对位置呢?为了解决这个问题作者提出一个相对位置的概念。
2. InDIGO
2.1 Relative Positions
为了解决绝对位置编码问题,作者提出相对位置 $r_{0:t}^t$ 来替代 $z_{0:t}^t$。$r_i^t \in \{-1, 0, 1\}^{t+1}$,且:
假设在 $t$ 时刻,对于第 $i$ 个词 $w_i$,用一个向量表示它的相对位置,每个维度取值只有 $(-1, 0, 1)$ 三种。$r_{i,j}^t$ 表示如果 $w_i$ 出现在 $w_j$ 的左边,则取 $-1$,如果出现在右边,则取 $1$,如果是同一个词,则取$0$。使用 $R^t=(r_0^t, r_1^t, …r_t^t)$ 表示序列中所有词的相对位置,每一列表示一个单词的位置向量,这个矩阵关于主对角线对称的元素其实是相反数。举个例子:
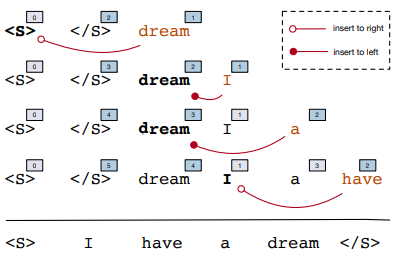
- $t=1$ 时,初始化序列:$y=(< s >, < /s >)$,初始化矩阵 $R=\left[\begin{array}{cc}0 & 1 \ -1 & 0 \end{array} \right]$ 。矩阵 $R$ 第一列 $r_0^1=[0,-1]$ 表示 $< s >$ 的相对位置向量:$< s >$ 相对于 $< s >$ 自身,因为是同一个词,所以取值为 $0$;$< s >$ 相对于 $< /s >$ 是在左边,所以取值为 $-1$。同理 $R$ 的第二列表示 $< /s >$ 相对位置向量。
- $t=2$ 时,$y = (< s >, < /s >, dream)$,$R = \left[\begin{array}{ccc} 0& 1& 1\ -1& 0& -1\ -1& 1& 0 \end{array}\right]$,$dream$ 相对于 $< s >$ 在其右边,所以相对位置向量第一维是 $1$;相对于 $< /s >$ 在其左边,所以相对位置向量第二维是 $-1$,相对于 $dream$ 自身,所以第三维是 $0$。
- $t=3$ 时,$y = (< s >, < /s >, dream, I)$,$R = \left[\begin{array}{cccc}0& 1& 1& 1\ -1& 0& -1& -1\ -1& 1& 0& -1\ -1& 1& 1& 0\end{array}\right]$,$I$ 相对于 $< s >$ 在其右边,第一维是 $1$;相对于 $< /s >$ 在其左边,第二维是 $-1$;相对于 $dream$ 在其左边,第三维是 $-1$,最后相对于自身,取值$0$。
- 以此类推…
$R$ 这样一个相对位置矩阵的最大优势是,在下一刻计算相对位置的时候这个矩阵不需要重新计算,因为下一个词无论插在哪里都不会影响之前的词的相对顺序,所以在更新 $R$ 的时候只需要给 $R$ 新增一行一列即可:
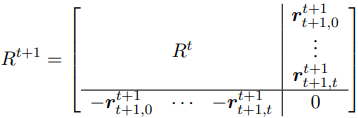
得到相对位置之后,我们就可以使用下式将相对位置映射成绝对位置了:
还以上面的例子加以说明:
- $t=2$ 时,$y = (< s >, < /s >, dream)$,$r_{< s >, j}^2 = (0, -1, -1)$,$z_{< s >}^2=\sum_j \max(0, r_{< s >, j}^2)=0$,所以 $< s >$ 的绝对位置是 $0$;$r_{< /s >, j}^2 = (1, 0, 1)$,$z_{< /s >}^2=\sum_j \max(0, r_{< /s >, j}^2)=2$,所以 $< /s >$ 的绝对位置是 $2$;$r_{dream, j}^2 = (1, -1, 0)$,$z_{dream}^2=\sum_j \max(0, r_{dream, j}^2)=1$,所以$dream$ 的绝对位置是 $1$。
- $t=3$ 时,$y = (< s >, < /s >, dream, I)$,$r_{< s >, j}^2 = (0, -1, -1, -1)$,$z_{< s >}^2=\sum_j \max(0, r_{< s >, j}^2)=0$,所以 $< s >$ 的绝对位置是 $0$;$r_{< /s >, j}^2 = (1, 0, 1, 1)$,$z_{< /s >}^2=\sum_j \max(0, r_{< /s >, j}^2)=3$,所以 $< /s >$ 的绝对位置是 $3$;$r_{dream, j}^2 = (1, -1, 0, 1)$,$z_{dream}^2=\sum_j \max(0, r_{dream, j}^2)=2$,所以 $dream$ 的绝对位置是 $2$;$r_{I, j}^2 = (1, -1, -1, 0)$,$z_{I}^2=\sum_j \max(0, r_{I, j}^2)=1$,所以 $I$ 的绝对位置是 $1$。
- 以此类推…
其实上面的式子的物理意义也很好理解:看相对位置向量中有多少个 $1$ 就表明该词在多少个词的右边,这样我们就可以知道该词所处的绝对位置了。
2.2 Insertion-based Decoding
给定一个长度为 $t$ 的序列 $y_{0:t}$ 以及相对位置 $r_{0:t}$ , 下一个词 $y_{t+1}$ 的相对位置的取值有 $3^{t+2}$ 种可能性,显然并不是任意一种可能性都能满足序列正确排序的要求的,我们需要找到最可能的 $r_{t+1}$。
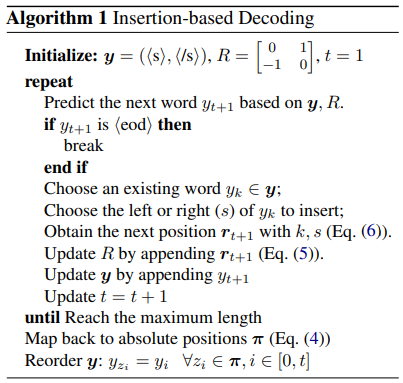
上图给出了一种算法框架:先从现有的序列中选取一个词 $y_k$, 其中 $0 \le k \le t$,然后向其左边或者右边插入 $y_{t+1}$,$r_{t+1}$ 由下式决定:
其中如果 $y_{t+1}$ 插入 $y_k$ 的左边,则 $s=-1$;如果 $y_{t+1}$ 插入 $y_k$ 的右边,则 $s=1$,然后更新 $R$。
继续用上面的例子说明:
- $t=1$ 时,假设我们选的 $y_k=< s >$,$y_{2}=dream$,其中 $k=0$,$j=k=0$ ,$dream$ 在 $< s >$ 的右边,所以 $r_{2, 0} = 1$;$j=1$,$r_{0, 1} = -1$,所以 $r_{2, 1}=r_{0, 1}=-1$,由于 $j=2$ 是$dream$ 本身,所以 $r_{2, 2}=0$。这样我们就得到了 $dream$ 的相对位置向量: $(1, -1, 0)$;
- $t=2$ 时,假设我们选的 $y_k = dream$,$y_3 = I$,其中 $k = 2$,$j=0$, $r_{2, 0}=1$,所以 $r_{3, 0} = 1$;$j=1$,$r_{3, 1}=r_{2, 1}=-1$;$j=2$,$j=k=2$,$I$ 在 $dream$ 的左边,所以 $r_{3,2}=-1$;$j=3$ 是 $I$ 自身,所以 $r_{3,3}=0$。这样我们就得到了 $I$ 的相对位置向量:$(1, -1, -1, 0)$;
- 依次类推…
上面这个公式的物理意义也是很好理解的:首先我们要确定 $y_{t+1}$ 要插在哪个位置,这个位置有两种表示方式:第一,slot,也就是用两个词形成一个空隙, $y_{t+1}$ 就插在这个空隙里面;第二,s,也就是一个词的左右,我们找到一个词 $y_k$,$y_k$有左右两侧,左边就是 $-1$, 右边就是 $1$。之前我们介绍的方法都是使用 slot,显然,这里使用的是 s。序列中其他的词对 $y_{t+1}$ 相对位置和对 $y_{k}$ 是一样的(因为不考虑 $y_k$本身的话, 实际上 $y_{t+1}$ 就是插在了 $y_k$ 的位置上),所以直接使用 $r_{k, j}$ 即可。比如 $t$ 时刻的序列是 $(A, B, C, D)$,推理 $t+1$ 时刻的时候 $y_k=C$,$y_{t+1}=E$,对于 $(A, B, D)$ 来说,我们是把 $E$ 插在了 $C$ 的位置上 $(A, B, D)$ 相对 $C$ 和 $D$ 的相对位置是一样的。
从上面的描述来看,我们现在还有两个问题没有解决:
- $y_k$ 怎么选择?
- $s$ 左右怎么确定?
这两个问题我们就需要通过模型结构来解决了。
3. Transformer-InDIGO
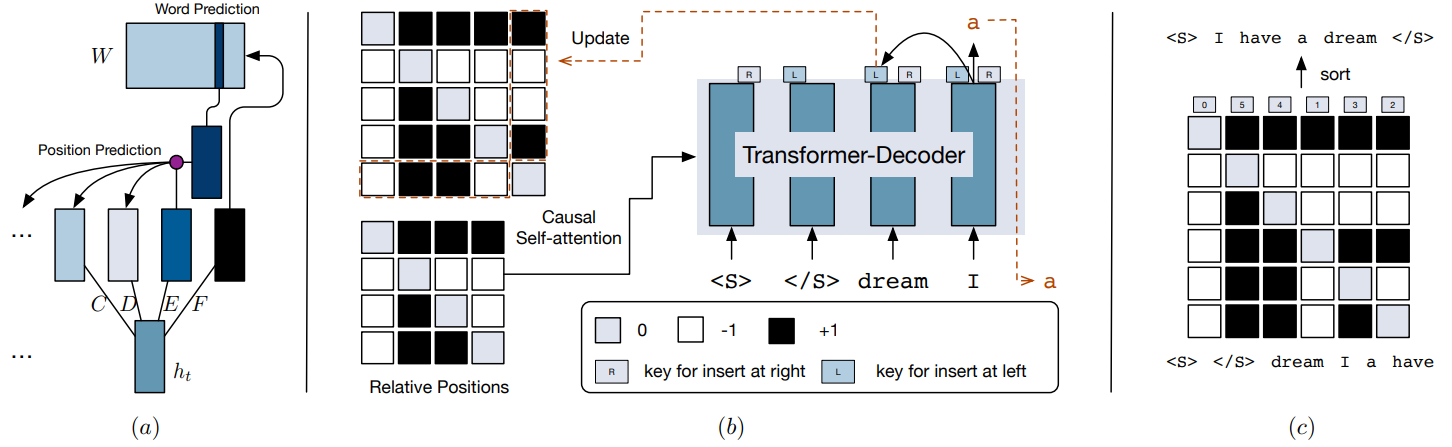
整个模型框架包含三部分:
- (a) —— 词和位置预测模块;
- (b) —— 相对位置矩阵更新;
- (c) —— 重排序后的序列输出。
在传统的 Transformer 结构中有一个零件叫做 positional encoding,这是一个绝对位置的编码,但现在解码器的绝对位置是未知的,所以这部分是需要进行修改的。
令 $U=(u_0, …, u_t)$ 表示 $y_{0:t}$ 序列经过 Embedding 之后的隐层,$R^t$ 是其对应的相对位置矩阵。修改后的注意开计算方法如下:
其中$Q, K \in \mathbb{R}^{d_{model}\times d_{model}}$,$A \in \mathbb{R}^{3 \times d_{model}}$ 是参数矩阵,$A_{[r_{i, j}+1]}$ 表示第 $r_{i, j}+1$ 列。
3.1 Word & Position Prediction
经过自注意力的计算之后我们得到一个矩阵 $H$,下一个词及其位置概率为:
也就是先预测下一个单词是什么,再预测它的相对位置。当然也可以倒过来,只是实验效果不如这个。
预测 $y_{t+1}$
其中 $W \in \mathbb{R}^{d_V \times d_{model}}$ 表示词向量矩阵,$d_V$ 表示词表大小,$F \in \mathbb{R}^{d_{model} \times d_{model}}$ 是用来将 $h_t$ 线性变换的权重矩阵。
预测 $k$
这里我们就要回答上一节我们遗留的两个问题 $y_k$ 和 $s$ 我们怎么确定?
其中 $C,D,E \in \mathbb{R}^{d_{model}\times d_{model}}$,$W_{[y_{t+1}]}$ 是 $y_{t+1}$ 的词向量。$C, D$ 是分别用来获取左、右的矩阵。注意我们最后得到的 $k_{t+1} \in [0, 2t+1]$,因为每个词都有左右两个位置。另外,为了避免 $y_{t+1}$ 出现在 $< s >$ 的左边和 $< /s >$ 的右边,作者手动设置 $p_{\mathrm{pointer}}(0|\cdot)=p_{\mathrm{pointer}}(2+t|\cdot) = 0$。
一个词在 $y_k$ 的右边实际上等价于在 $y_{k+1}$ 的左边。那其实这两个预测结果都是对的。虽然最后的 $r$ 向量都是一样的。
相对位置的更新和输出序列的重排序我们前面已经介绍了,这里就不再赘言。
3.2 Learning
因为一个句子的可能排列顺序太多了,不可能一一枚举,所以这里最大化 ELBO(evidence lower-bound ) 来代替最开始的概率之和。
对于输入 $x$ 和输出 $y$,首先定义一个生成顺序 $\pi$ 的近似后验 $q(\pi|x, y)$。然后 ELBO 可以表示为:
其中 $\pi = r_{2:T+1}$, 表示从 $q(\pi|x, y)$ 中采样的相对位置, $\mathcal{H}(q)$ 表示熵项,如果 $q$ 是固定的,那么这一项可以忽略。
为了计算位置损失,作者这里定义:
$k^l$ 和 $k^r$ 就是我们前面讲的 $y_k$ 的右边等价于在 $y_{k+1}$ 的左边。
然后就可以根据近似后验来进行采样,优化这个函数了,那么这个近似后验怎么定义呢?作者这里考两种方法:
常见的确定顺序,如下表:
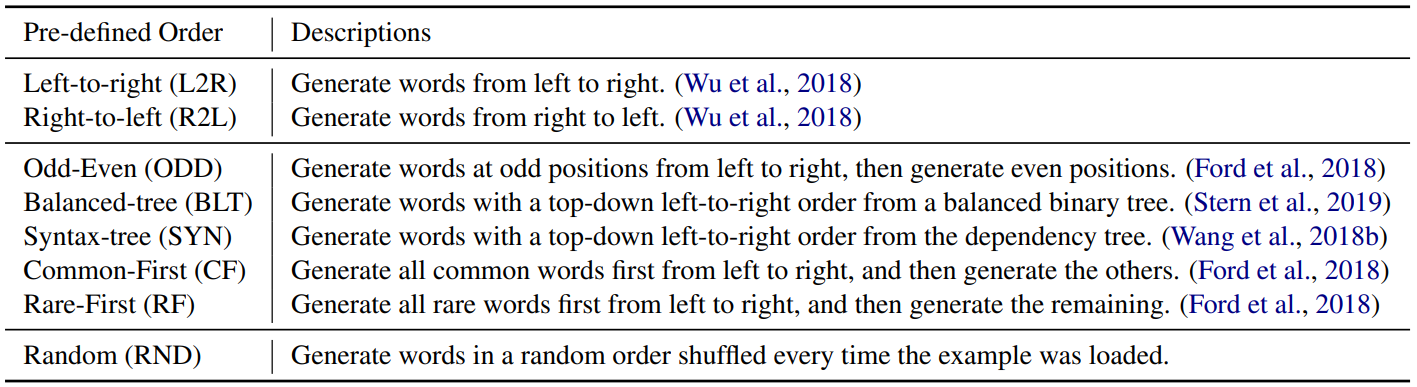
这种情况下,模型其实就变成了和普通的序列生成模型差不多了,只用最大化一个生成顺序的概率就行了,区别就是多了相对位置编码。
Searched Adaptive Order (SAO),其实就是 beam search。传统的序列生成模型其实也有 beam search,不过那是在每个时刻解码概率最大那些子序列。 而这里的 beam search 空间更大,搜索的是整个排列的空间。 也就是在每个时刻,遍历所有的下一个单词和它的相对位置,找出最大的 $B$ 个子序列。 最后的目标函数变为了:
这里作者假设:
上面的 beam search 可以帮助我们找到贪心下最优的生成顺序,但是,同时也减少了生成全局最优的可能性,为此,我们可以在 beam search 的同时加入 dropout。
在实际的实验中,用上面的方法导致模型生成很多标点和功能符号,这是因为位置预测模块的学习比字符预测模块的学习快得多。为此,我们可以用一种固定顺序如 L2R 去预训练整个模型,然后再用SAO 去微调。
现在我们可以由模型生成任意顺序了,但是,这种方法有一个问题:不能并行。因为该方法还是需要一个一个去生成字符和位置。
4. Experiments
实验主要做了机器翻译、词序还原、代码生成和图像标签生成,这里就简单看一下机器翻译结果,其他的详见论文。
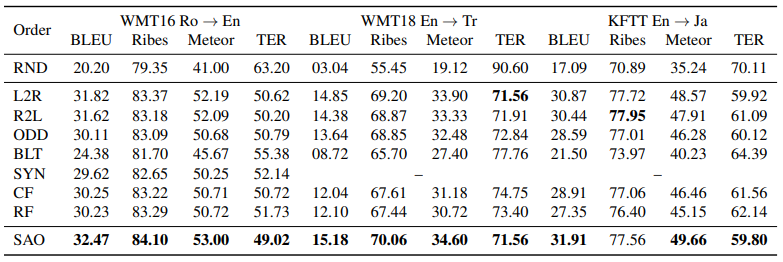
这里,中间的若干行都是不同的自回归生成策略。可以看到,在三个数据集和各种指标下,SAO 都比自回归好。下面给出一个实际的例子:

Reference
Insertion-based Decoding with automatically Inferred Generation Order, Jiatao Gu , Qi Liu , Kyunghyun Cho. 2019. arXiv: 1902.01370
香侬读 | 按什么套路生成?基于插入和删除的序列生成方法, 香侬科技, 知乎
- 论文赏析[TACL19]生成模型还在用自左向右的顺序?这篇论文教你如何自动推测最佳生成顺序, godweiyang, 知乎
- Insertion-based Decoding with Automatically Inferred Generation Order #122, kweonwooj, Github Pages



