
之前我们介绍的两种 insertion-based 文本生成方法预先规定了每次生成最中间的词,这样一来我们虽然利用树实现了并行,但是却丢失了其中的生成模式,我们不知道模型在生成的时候经历了什么。那么我们能不能让模型自动生成一棵树呢?比如,现在生成了一个根节点,然后再生成左右子节点,然后再生成子节点的子节点,以此类推,但不同的是,这棵树不一定平衡,甚至可能退化成一条链,但我们获得了模型的生成模式,如下图所示:
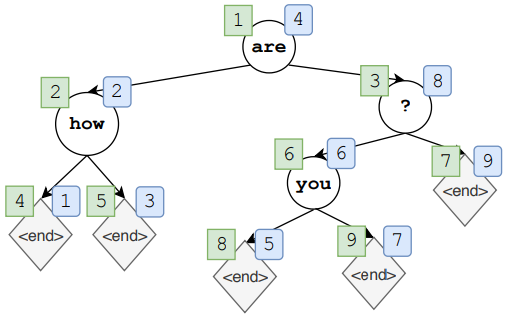
- 可以从任意位置开始生成;
- 图中绿框中的数字表示生成顺序;
- 图中蓝筐中 的数字表示重构顺序;
- 传统的从左向右被做为二叉树的一种特殊情况。
1. Abstract Framework
- $Y=(w_1, …, w_N)$ ——表示生成的序列,其中 $w_i \in V$,是一个词表;
- $\tilde{V} = V \bigcup \{< end >\}$ —— 表示所有可能生成的字符串;
- $S = \tilde{V}^*$ —— 表示序列的状态空间;
- $s \in S$ —— 表示状态空间中的一个序列,该序列中每个元素都来源于 $\tilde{V}$。比如上图 $s_1=(are), s_2=(are, how),…,s_4=(are, how, ?, < end >)$;
- $a$ —— 表示将 $\tilde{V}$ 中的一个元素添加到 $S$ 后面的操作;
- 所有的叶子结点都是 $< end >$ 时表示序列生成过程的结束,此时 $T=2N+1$,其中 $N$ 表示序列中非 $< end >$ 的元素, $T$ 表示整个序列的长度, $s_T$ 表示最终状态。
- $\tau(t)$ —— 表示按层序遍历树上的第 $t$ 的节点,则 $(a_{\tau(1)},…,a_{\tau(T)})$;
- 以上图为例,最终的序列是将图中蓝筐中的数字映射成绿框的顺序,然后删掉所有的 $< end >$。
- $\pi(a|s)$ —— 表示根据给定一个序列状态生成一个 $a$ 操作的策略。我们知道树的遍历有很多种方式,因此对于同一个序列,我们可以有不同的树,我们就有多种生成模式。
2. Learning for Non-Monotonic Generation
我们考虑两种情况下的文本生成:
- 非条件生成:类似语言模型,没有额外信息输入;
- 条件生成:类似机器翻译,根据输入序列生成新的序列。
我们先考虑非条件生成的情况。这种情况比较复杂,因为我们只知道最终的序列是什么样的,但是生成这样的序列的那棵树长什么样子我们并不知道。因为我们是通过遍历树的叶子结点得到最终的序列,而树的遍历有很多种方法,要用不同的遍历方法得到同一个序列,此时树的结构就不尽相同。树的结构不同意味着每次生成都会有多种操作的可能性,这样我们就不能使用传统的监督学习方法了。为了解决这个问题我哦们可以使用 learning-to-search 和 imitation learning。
Key Idea
假定我们只有一个序列 $Y$。现在的想法是,在第一步我们首先生成任意一个单词 $w \in Y$ 作为整棵树的根节点,然后类似快速排序的思想,在 $w$ 左边和右边递归地生成,由于我们希望树的中序遍历可以得到原始序列 $Y$,所以 $w$ 左边的字符必须在 $w$ 的左子树,同理对右子树。然后用 direct loss minimization 及相关的技术学习一个参考策略 $\pi^{\ast}$ 当成当前策略 $\pi $ 的首选策略。
2.1 Unconditional Generation
所谓 Learning-to-search,就是模仿一个参考策略 $\pi^{\ast}$ 来学习当前策略 $\pi$。我们定义一个输入策略(roll-in)$\pi^{in}$ 和一个输出策略(roll-out)$\pi^{out}$。下面我们不断从 $\pi^{in}$ 中抽样状态 $s$,然后在 $\pi^{out}$ 下对每个行为 $a$ 计算一个运行代价,之后学到的 $\pi $ 被训练去最小化这个运行代价。
用数学语言来说就是:
- $U(T)$ 表示 $[1,…,T]$ 的均匀分布;
- $d_\pi^{in}$ 表示在 $\pi$ 策略下进行 $t$ 步得到的状态分布;
- $C(\pi;\pi^{out}, s)$ 表示运行代价
通过选择不同的 $\pi;\pi^{out}, s$ 我们可以得到不同的 learning-to-search 算法,我们希望找到一个策略能够在获得 $s_t$ 上表现得和 $\pi^*$ 一样好,甚至更好。
$\pi^{in}$ 的选择
$\pi^{in}$ 决定了我们要学习的策略 $\pi$ 训练的状态分布。我们可以选择 $\pi$ 与 $\pi^{out}$ 的混合作为 $\pi^{in}$,也可以选择仅使用 $\pi^{out}$ 。后者更简单,我们本着从简的原则,使用后者。
$\pi^{out}$ 的选择
$\pi^{out}$ 就是我们要模仿的策略。由于 $\pi^{out}$ 是参考策略,所以我们可以通过 $\pi ^{out}$ 完全根据序列构建出树,于是我们可以把 $\pi^{out} $ 视为树的生成过程,在每一步都对应一个状态 $s_t$ 和序列 $Y_t$ 。在每个 $s_t$ ,$Y_t$ 包含了合法行为,比如下图,在第一步,我们可以选择生成 $(a, b, c, d)$ 中的一个,比如我们选择了 $b$,之后,左节点的选择就只有 $a$ 了,右节点的选择就有 $(c,d)$,这些选择就是“合法”的。
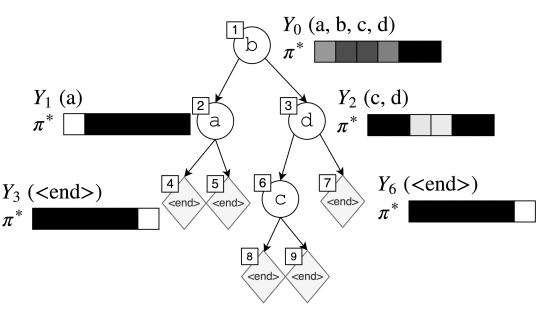
给定一个连续子序列 $Y_t=(w_1’, …, w_{N^{‘}}’)$,$\pi^{out}$ 可以定义为:
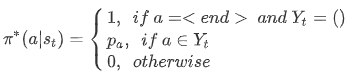
其中 $\sum_{a \in Y}p_a=1$。我们可以看到 $\pi^{out}$ 策略主要由 $p_a$ 决定,这里作者预定义了三种不同的策略:均匀策略(或者任意顺序策略,uniform oracle)、指导策略(coaching oracle)和退火指导策略(annealed coaching oracle)。
均匀策略
令 $p_a = 1/n$,记为 $\pi^{\ast}_{\mathrm{uniform}}$。
指导策略
任意顺序的策略会导致一个问题:难以使得 $\pi $ 去模仿。为此,我们可以考虑加入当前学习的策略 $\pi $:
这样一来,既可以避免不合法的行为,也可以按照当前策略 $\pi $ 继续学习。
退火指导策略
指导策略也有一个问题:它不会引导模型进行多样化的学习。因此,我们可以再适当加入$\pi^{\ast}_{\mathrm{uniform}}$:
这里 $\beta$ 随着训练从1线性递减到0。
$C$ 的选择
$C$ 度量的是经过输入策略的选择得到的状态与输出策略之间的误差,最常见的方法是使用平方误差。然而,有研究表明使用 RNN 时平方误差表现不佳,所以我们可以转而使用 KL 散度:
2.2 Conditional Generation
上面说的是给定单个句子 $Y$ ,如果我们要学习 $X \rightarrow Y$ 怎么办呢?
我们将条件输入 $X$ 编码成一组 $d_{enc}$ 维的向量,记为 $f^{enc}(X)$,然后经过神经网络,比如 LSTM 或者 Transformer,得到隐状态向量 $H \in \mathbb{R}^{|X| \times d_{enc}}$,然后再送入该模型中即可。
3. 神经网络结构
作者选择使用神经网络实现上面的二叉树生成策略,因为神经网络能有效的对不同尺寸的输入进行编码以及预测输出。这里作者选择两种神经网络:LSTM 和 Transformer,一个是老一代的 NLP 武林盟主,一个是新生代江湖俊杰。
3.1 LSTM Policy
将二叉树的层序遍历节点 $(a_1, …, a_t)$ 作为序列输入到 LSTM ,然后 LSTM 将序列编码成向量 $h_t$,然后计算 $a_i$ 的概率分布:
3.2 Transformer Policy
同样是将 $(a_1, …, a_t)$ 作为输入,然后使用多头注意力计算 $h_t$,再计算 $a_i$ 的概率分布。
3.3 Auxiliary $< end >$ Prediction
作者将 $< end >$ 的预测和 $a_i$ 的预测分开进行,先利用伯努利分布判断是否是 $< end >$,设定一个阈值 $\tau$ ,当概率大于 $\tau$ 时,则认为 $a_t = < end >$,否则根据 $\pi$ 计算 $a_t$。
4. Experiments
作者最后在多个任务上进行了实验:
- 语言模型
- 句子补齐
- 词序重排
- 机器翻译
这里展示几个生成样例。
- 语言模型
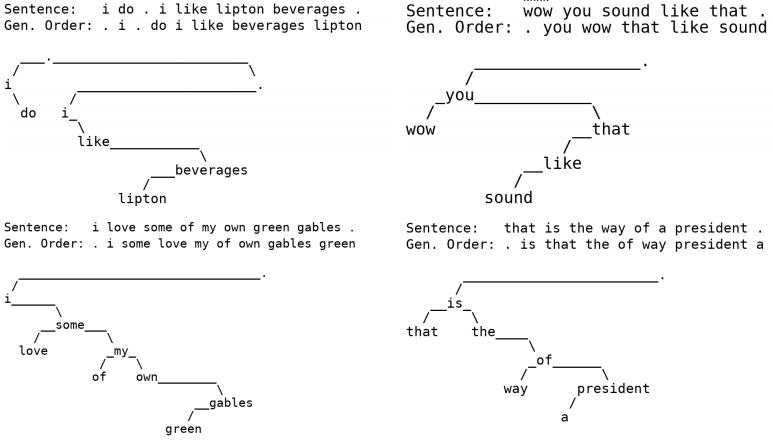
- 机器翻译
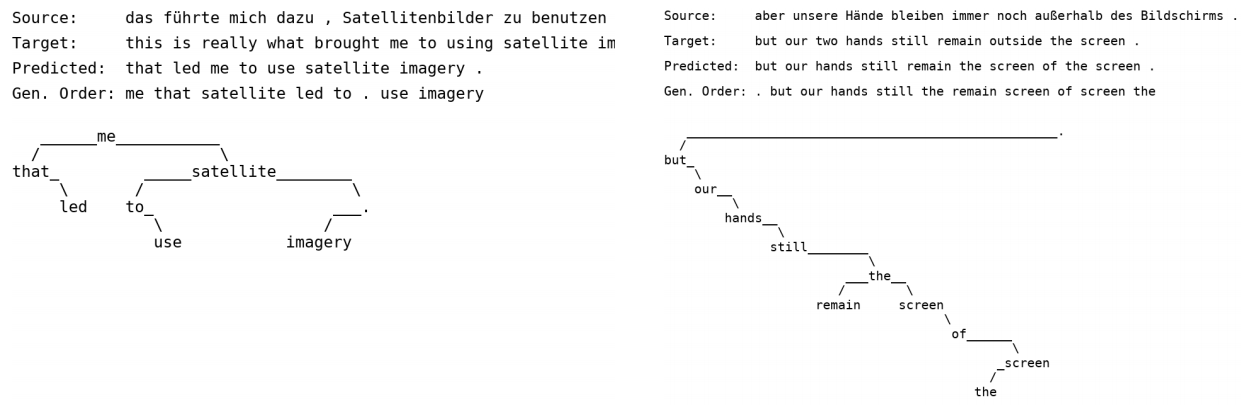
从图中我们可以清晰地看到生成模式。更多详细的实验可以去看原文。
Reference
- Non-Monotonic Sequential Text Generation, Sean Welleck, Kiante Brantley, Hal Daume III, Kyunghyun Cho. 2019. arXiv: 1902.02192
- Non-Monotonic Sequential Text Generation #121, kweonwooj. Github Pages. 2019
- 香侬读 | 按什么套路生成?基于插入和删除的序列生成方法, 香侬科技,知乎



