
我们注意到 Insertion Transformer 提出一种很有意思的文本生成框架:Insertion-based 。但是它仍然使用的是Encoder-Decoder 框架,这种框架有一个缺陷,就是 $(x, y)$ 无法对 联合概率 $p(x, y)$ 进行建模。对此 William Chan 等人于 2019 年提出一种新的架构:KERMIT,该模型抛弃了传统的 Encoder-Decoder 架构,使得我们能对 $p(x, y)$ 联合概率进行建模。训练阶段可以通过句子对 $(x, y)$ 获得联合概率 $p(x, y)$,也可以通过非句子对分别获得边缘概率 $p(x)$ 或者 $p(y)$。推理阶段我们可以获得条件概率 $p(x|y)$ 和 $p(y|x)$。
1. Abstract Framework
KERMIT 算是 Insertion Transformer 的泛化版,损失函数用的是平衡二叉树,解码同样可以采用贪心解码和并行解码两种方式。
- 序列:$x=(x_1,…,x_n)$;
- 生成 $x$ 的顺序:$z \in \mathrm{permut}(\{1,…,n\})$,其中 $\{1,…,n\}$ 对应的是 $x$ 中每个词的绝对位置索引。$z$ 属于位置索引的排列组合,即 $x$ 中元素的生成顺序;
- 对应序列:$((c_1^z, l_1^z), …, (c_n^z, l_n^z))$,其中 $c_i^z \in C$ 是词表中的词,$1 \le l_i^z \le i$ 是目前序列的插入相对位置。
- $(x_1^{z, i}, …, x_i^{z, i})$,表示在 $\{z_1, …, z_i\}$ 顺序下 $x$ 的子序列。
KERMIT 对输出的词和词的位置进行建模:
举个例子:
序列 $x = (A, B, C)$ 的生成顺序是 $() \rightarrow (C) \rightarrow (A, C) \rightarrow (A, B, C)$,那么 $z = (3, 2, 1)$,对应序列为 $(c_1^z, l_1^z)=(C, 1), ~(c_2^z, l_2^z)=(A, 1), ~(c_3^z, l_3^z)=(B, 2)$。注意 $z$ 和 $l$ 都表示元素的索引,不同的是 $z$ 表示的是完整序列位置的索引,$l$ 表示的是序列生成过程中,当前序列的位置索引。此时 $(x_1^{z,2}, x_2^{z,2})=(A, C)$。
2. KERMIT
有了以上定义,我们就可以得到:
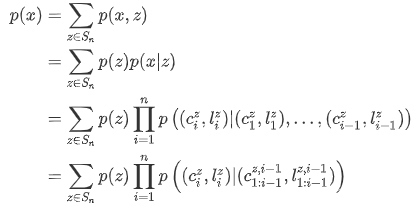
最后一步使用了 Markov 假设:插入的顺序不重要,只是一个结果。对于 $p(z)$ 我们使用均匀分布,其他部分使用平衡二叉树(详见Transformer家族之Insertion Transformer)。
2.1 Learning
上式要直接求解比较麻烦,但是可以用 Jensen 不等式得到 $p(x)$ 的下限:
带入刚刚得到的 $p(x|z)$ 表达式:
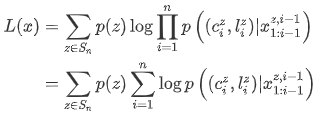
下面将 $L(x)$ 分成是三部分:$(z_1,…,z_{i-1})$ 表示之前的插入,$z_i$ 表示下一步插入,$(z_{i+1}, …,z_n)$ 表示以后的插入:
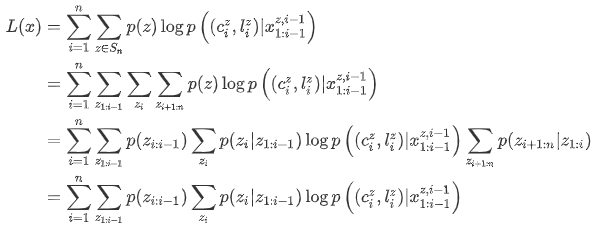
最后一步是由于 $\sum_{z_{i+1:n}}p(z_{i+1:n}|z_{1:i})=1$。
通过下面几个简单的采样过程就可以计算 $L(x)$:
- 采样生成步骤 $i \sim \mathrm{Uniform([1, n])}$;
- 采样前 $i-1$ 次插入操作的排列组合 $z_{1:i-1} \sim p(z_{1:i-1})$;
- 计算 $\log p\left((c_i^z, l_i^z)|x_{1:i-1}^{z,i-1}\right)$,$p(z_i|z_{1:i-1})$,二者相乘然后乘以 $n$。
前两步不多说,说下最后一步。
$i=1$,则 $\log p\left((c_1^z, l_1^z)|x_{1:0}^{z,0}\right)=\log p\left((C, 1)|(< BOS >)\right)$,$p(z_1|z_{1:0})=p(3|< BOS >)$;
$i=2$,则 $\log p\left((c_2^z, l_2^z)|x_{1:1}^{z,1}\right)=\log p\left((A, 1)|(< BOS >, C)\right)$,$p(z_2|z_{1:1})=p(1|(< BOS >, 3))$;
$i=3$,则 $\log p\left((c_3^z, l_3^z)|x_{1:2}^{z,2}\right)=\log p\left( (B, 2)|(< BOS >, A, C)\right)$,$p(z_3|z_{1:2})=p(2|(< BOS >, 3, 1))$;
2.2 Inference
- Greedy decoding
- Parallel decoding
2.3 Pairs of Sequences
目前为止我们讨论的都是单个序列。我们可以通过将两个序列拼接在一起实现对 $(x, y)$ 的直接建模,即:
比如,$x=(A,B,C,< EOS >),~y=(A’,B’,C’,D’,E’,< EOS >)$,拼接后成为 $(x, y)=(A,B,C,< EOS >, A’,B’,C’,D’,E’,< EOS >)$。相对于 Encoder-Decoder 结构,这样的好处是,$x, y$可以互为源序列和目标序列。
对于多模态数据,这种结构可能会成为未来的趋势。
通过这种结构我们可以很轻易的对 $p(x, y)$ 联合概率进行建模,同时还能获得边缘概率 $p(x),p(y)$ 以及条件概率 $p(x|y), p(y|x)$。我们还可以进行针对性的训练:
- 如果给出完整的 $x$ 或 $y$ (没有拼接成一个序列),则可以训练条件概率;
- 如果 $x$ 或 $y$ 有一个为空,则训练边缘概率。
2.4 Model
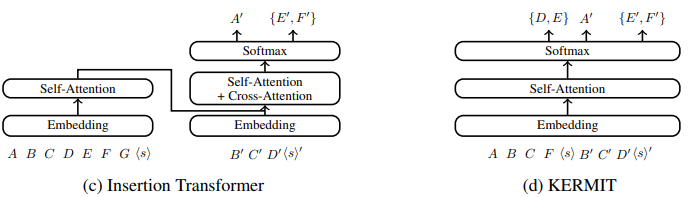
KERMIT 的大致结构如图所示,采用 Transformer 的Decoder 部分,并且去掉了掩码注意力层。由于没有 Encoder ,所以注意力层是完全的自注意力层,不需要和 Encoder 进行 cross-attention。
另外,KERMIT 的损失函数用的是平衡二叉树,最后计算 $p(c, l)$ 的时候用的是 Insertion Transformer 中的因式分解方法。
所以我们可以认为 KERMIT 是 Insertion Transformer 的泛化版,很多后者不具备的能力都可以在它身上找到。尤其是在翻译领域,这种对称式的多模态训练很可能会成为未来的趋势。
比如:输入源序列 $(x, y)$ 分别是 $(en,zh)$,输出目标序列是 $(zh,en)$。这样我们相当于在一个模型上实现了两种语言的互相翻译。
3. Experiments
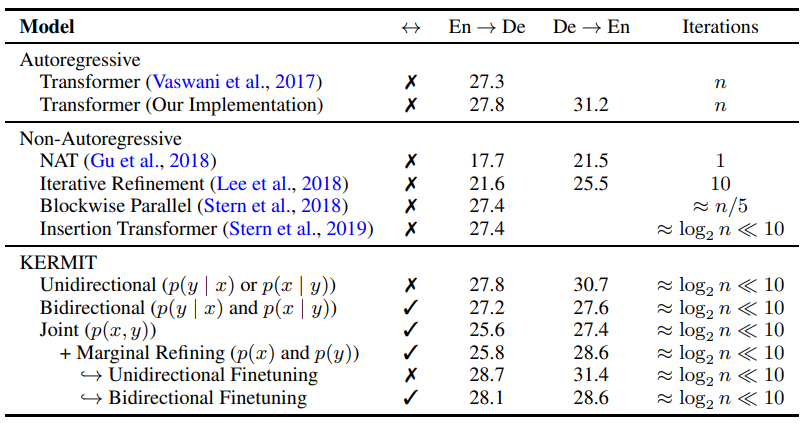
- Unidirectional 表示和传统方法一样,输入单一序列,输出单一序列;
- Bidirectional 表示输入单一序列,输出单一序列,但是在同一个模型中训练两种语言;
- Join 表示两种序列拼接在一起输入模型,另外使用 $p(x),p(y)$ 进行改善,输出同样也是单一序列和两种序列。
Reference
- KERMIT: Generative Insertion-Based Modeling for Sequences, William Chan , Nikita Kitaev, Kelvin Guu , Mitchell Stern , Jakob Uszkoreit, 2019, arXiv: 1906.01604
- 香侬读 | 按什么套路生成?基于插入和删除的序列生成方法,香侬科技,知乎



