
传统的文本生成,比如机器翻译无论是自回归或者半自回归的推理方式,都有一个特点:通常是自左向右依次生成文本序列。本文将介绍一篇文章,打破思维定式,突破自左向右的顺序生成。Insertion Transformer采用随机插入式序列生成:
- 以任意顺序生成;
- 支持自回归或者半自回归生成(同时在不同位置插入)。
Insertion Transformer不仅在效果上远超非自回归模型,而且能以$log(n)$的推理速度,效果上达到原始Transformer的水平。
1. Abstract Framework
- $x$ —— 源序列
- $y$ —— 目标序列
- $\hat{y}_t$ —— $t$ 时刻的输出序列,由于我们只有插入操作,因此 $\hat{y}_t$ 必须是最终输出序列的子序列,比如如果最终输出序列是$[A, B, C, D, E, F]$,那么$\hat{y}_t=[B, C]$ 是合法的,而$[C, B]$则不可以
- $\hat{y}$ —— 最终输出序列
- $C$ —— 词表
- $c$ —— $c \in C$,上下文
- $l$ —— $l \in [0, |\hat{y}_t|]$,需要插入词的位置
Insertion Transformer 需要对输出的词和词的位置都要进行建模:
举个例子:
假设$\hat{y}_t = [B, D]$,$p(c, l| x, \hat{y}_t) = (c=C, l=1)$,也就是说把 $C$ 插入到 $\hat{y}_t$的 索引值为1的地方(从0开始计算索引),这就意味着$\hat{y}_{t+1} = [B, C, D]$。
2. Insertion Transformer
- Full Decoder Self-Attention
将 Transformer 中的 causal self-attention 替换为 full self-attention。
- Slot Representation via Concatenated Outputs
标准的 Transformer 是给输入 $n$ 个词,然后模型输出 $n$ 个向量,然后取最后一个词作为输出序列的下一个词。而为了实现插入操作,作者对 decoder 做了修改。因为插入需要的是在词与词之间插入,也就是说,decoder 需要对slot 进行编码,$n$ 个词就有 $n+1$ 个 slot,也就是说给定 $n$ 个词,decoder 输出必须是 $n+1$ 个向量:$n$ 个词之间有 $n-1$ 个slot,而序列开始和结束的地方还有两个 slot,一共 $n+1$ 个slot。
比如:$[A, C, E]$ 一共有3个词,$A, C$和$C, E$之间两个slot,模型下一个预测的词也有可能需要插入到$A$之前,或者 $B$ 之后,所以 $A$ 前和 $B$ 后还有两个slot,3个词4个 slot。
为了实现这一目标,我们在 decoder 的输入序列上加入特殊的开始和结束符,比如<BOS>或者<EOS>。这样我们就构造了一个 $n+2$ 的输入序列,最终 decoder 也将输出 $n+2$ 个向量。然后我们再将相邻的两个向量拼接在一起,这样就形成了 $n+1$ 个向量了。每个向量代表一个 slot。因此,每个 slot 相当于综合了该位置前后两个词的语义。
举个例子:
- 给定 $[A, C, E]$;
- 加入
<BOS>和<EOS>,成为 $[< BOS >, A, C, E, < EOS >]$; - 输入给decoder;
- decoder 输出 $[[1,2,3], [2,3,4], [3,4,5], [4,5,6], [5,6,7]]$;
- 将相邻的两个向量拼接起来:$[[1,2,3,2,3,4],[2,3,4,3,4,5],[3,4,5,4,5,6],[4,5,6,5,6,7]]$;
2.1 Model Variants
得到了 slot 向量,怎样得到最终的 $p(c, l)$,作者对此也进行了一番探索。
在继续介绍之前,我们先定义一些变量:
- $H$ —— $H \in \mathbb{R}^{(T+1) \times d}$,表示上面我们得到的 slot 特征矩阵, 其中 $d$ 是向量维度,$T$ 是输入序列长度;
- $W$ —— $W \in \mathbb{R}^{d \times |C|}$,是标准的 softmax 投影矩阵,其中 $|C|$ 表示词表大小。
好了,我们继续下面的介绍。
- Content-Location Distribution
为了得到 $p(c, l|x, \hat{y}_t)$,作者提出两种方法:第一种是直接对 $(\mathrm{content}, \mathrm{slot})$进行建模;另一种方式是因式分解。
- 直接建模
注意这里得到的是一个$(T+1) \times |C|$ 的矩阵,其物理意义为:在$(T+1)$ 个slot 的每个位置上最可能出现的词。
- 因式分解
我们可以利用条件因式分解得到:
其中 $h_l \in \mathbb{R}^{d}$ 表示 $H$ 的第 $l$ 行,$q \in \mathbb{R}^{d}$ 表示一个可学习的 query 向量。
这种方法的好处是相对直接建模的方式内存消耗要小得多。
- Contextualized Vocabulary Bias
为了增加 slot 之间的信息共享,我哦们可以在 $H$ 上增加一个最大池化的操作,得到一个上下文向量 $g \in \mathbb{R}^d$,然后用一个可学习的投影矩阵 $V \in \mathbb{R}^{d \times |C|}$ 将 $g$ 投影到词表空间: $b=g \cdot V \in \mathbb{R}^{|C|}$,将 $b$ 作为偏置量添加到每个位置上。整个过程如下:
- Mixtrue-of-Softmaxes Output Layer (Optional)
讲道理,这部分我没有太想明白为什么需要 MoS。如果是从语言模型本身的复杂性来考虑,MoS 确实有可能会起到效果, 但是如果从同时编码 $(c, l)$ 的角度考虑的话,我就不太明白了。从文章的实验结果来看,这部分修改并没有使模型达到最佳效果(当然如果只考虑以上三种变种的话,加上 MoS 确实有提升效果,但是加上后续的一些 tricks 综合整个模型试验,它并没有达到最佳效果)。因此,这里对 MoS 做简单介绍吧,更详细的内容请去读原文。
假设我们有一个上下文矩阵 $H \in \mathbb{R}^{N \times d}$,一个词向量矩阵 $W \in \mathbb{R}^{|C| \times d}$,其中 $|C|$ 是词表大小。给定上下文,我们希望从矩阵 $A$ 中去预测下一个词 $p(x|c)$,其中 $A \in \mathbb{R}^{N \times |C|}$。我们的模型是希望通过从真实的世界中采样 $N$ 个样本,训练出尽可能接近 $A$ 分布的 $A’$ 矩阵。
我们希望 $A’ = HW^T$,尽量接近 $A$ 的分布。
矩阵乘法有一个性质:两矩阵乘积的秩(rank)等于两个矩阵秩较小的那个:
通常我们的训练样本 $N$ 会远远大于词向量的维度,也就是说 $A’$ 的秩的上限由词向量维度 $h$ 决定的。而真实世界的 $A$ 的秩很可能接近 $|C|$,通常 $|C| \gg d$。这就造成一个问题,我们希望通过 $A’$ 来逼近 $A$ 的分布,但是实际上$A’$ 的秩是远低于 $A$ 的,也就是说我们的模型训练出来的矩阵表达能力是远低于真实世界的。
简单一句话就是:由于词向量维度的限制,我们训练出来的模型表达能力不足以完整的描述真实的世界。
要解决这个问题的最直接的方法就是让词向量的维度等于词表的大小,即 $d = |C|$。但这会引入另外一个问题,那就是参数量爆炸!。
因此,作者提出 Mixture of Softmax:
其中 $\sum_{k=1}^K\pi_{c, k}=1$。
这里引入了两个权重:
- $P \in \mathbb{R}^{Kd\times d}$,它将 $\mathbf{h}$ 映射成 $K$ 个不同的 $\mathbf{h}$,每个 $\mathbf{h_k} \in \mathbb{R}^d$;
- $M \in \mathbb{R}^{d \times K}$,决定这 $K$ 个模型如何混合。
这个模型的基本原理就相当于使用 $K$ 个 softmax 将它们混合起来,既避免了参数量爆炸,又保持了模型的表达能力。这 $K$ 个不同的模型组合求加权平均效果往往比单一的模型要好, $K$ 个模型联合训练也能避免一些单模型的缺陷。
3. Training and Loss Functions
Insertion Transformer的机制支持它以任何顺序来生成目标语句,因此在训练时,可以通过设计loss function来将先验的顺序信息施加给模型,从而使得模型在预测时也按照先验的顺序进行预测。
3.1 Left-to-Right
文中将原始自回归模型从左到右的生成方式作为一个特例进行对比。固定每次插入的单词位置都在最右侧,就退化成了原始的序列生成方式。
3.2 Balanced Binary Tree
显然从左到右的解码方式不能做到并行。因此,作者提出使用平衡二叉树的方式最大化并行解码能力。基本思想是:每次生成目标序列最中间的词。
比如,目标序列是 $[A, B, C, D, E, F, G]$,解码的顺序是:
- $[]$;
- $[D]$;
- $[B, D, F]$;
- $[A, B, C, D, E, F, G]$。
为了达到这个目的,作者提出 soft binary tree loss:
随机挑选一个 $k$ 值,$k \sim \mathrm{uniform}(0, |y|)$;
打乱 $y$ 中每个词的索引顺序,选择其中前 $k$ 个索引对应的词,这样就得到了一个长度为 $k$ 的子序列;
这个长度为 $k$ 的子序列包含 $k+1$ 个slot,每个 slot 对应的位置为 $l = 0, 1, …, k$。令 $(y_{i_l}, y_{i_l+1}, …, y_{j_l})$为 $ y$ 中剩余的对应第 $l$ 个 slot 位置上的词。
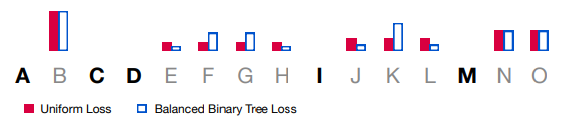
以上图为例:解释$(y_{i_l}, y_{i_l+1}, …, y_{j_l})$是什么?$[A, C, D, I, M]$ 是随机挑选出来的子序列,
- $l=1$ 对应的 $(y_{i_1}, y_{i_1+1}, …, y_{j_1})=[B]$;
- $l=3$ 对应的 $(y_{i_3}, y_{i_3+1}, …, y_{j_3})=[E, F, G, H]$;
- $l=4$ 对应的 $(y_{i_4}, y_{i_4+1}, …, y_{j_4})=[J, K, L]$;
- $l=5$ 对应的 $(y_{i_5}, y_{i_5+1}, …, y_{j_5})=[N, O]$;
对于$l=0, 2$ 的情况在后面讨论。
注意 $i_l, j_l$ 分别是该词在原始 $y$ 中的索引。
得到了 $(y_{i_l}, y_{i_l+1}, …, y_{j_l})$ 列表以后,我们去计算每个 slot 与其对应的$(y_{i_l}, y_{i_l+1}, …, y_{j_l})$ 中每个词的距离:
$l=1$ : $d_1 = \left|\frac{1+1}{2}-i|_{i=1}\right| = [0]$;
$l=3$ : $d_3 = \left|\frac{4+7}{2}-i|_{i=4,5,6,7}\right| = [1.5, 0.5, 0.5, 1.5]$;
- $l=4$ : $d_4 = \left|\frac{9+11}{2}-i|_{i=9,10,11}\right| = [1,0,1]$;
- $l=5$ : $d_5 = \left|\frac{13+14}{2}-i|_{i=13,14}\right| = [0.5, 0.5]$;
然后我们根据上面计算出来的距离,给每个距离一个权重:
有了上面的权重,我们就可以定义每个位置上的 slot loss 了:
最后总的 loss 为:
SlotLoss 中的 $\tau$ 是一个温度超参数,用来控制 $w_l$ 的平滑程度的:当 $\tau \rightarrow 0$ 时,将会给最中间的位置以非常高的权重,两侧的位置权重几乎为 0;当 $\tau \rightarrow \infty$ 时,每个位置的权重基本相等。
3.3 Uniform
作者也做了不给模型施加约束,让模型自己探索生成方式的尝试,即鼓励模型uniform地生成每个slot中的各个单词。实现的方式很简单,将$\tau \rightarrow \infty$ 即可。
3.4 Termination Condition
选取解码时的停止条件也是一个很关键的问题。Insertion Transformer 提出了两种停止条件:
Slot Finalization 在训练时引入了 end-of-slot token,来和 label 为空的 slot 计算损失函数。在推理时,当且仅当全部 slot 的预测都为 end-of-slot 时,停止继续解码。
上面我们在介绍 soft binary tree loss 的时候遗留了一个问题:$l=0, 2$ 时怎么办?我们看到当 $l=0, 2$ 时我们不需要插入任何词,这时候我们定义一个 end-of-slot token,这个时候 $l=0, 2$ 对应的 $(y_{i_1}, y_{i_1+1}, …, y_{j_1})=[\mathrm{EndOfSlot}]$ ,然后我们用 $\mathrm{EndOfSlot}$ 计算损失。推理的时候,当所有的 slot 对应的 $y_{i_l}$ 都是 $\mathrm{EndOfSlot}$ 时停止解码。
Sequence Finalization 则还是用的传统的 end-of-sequence token,在全部单词都生成之后,将每个 slot 都和 end-of-sequence token 计算损失函数。在推理时,当任意一个 slot 的预测结果是 end-of-sequence token 时,停止解码。
回到上面那个 $l=0, 2$ 的问题,在上面使用 Slot Finalization 时,我们令 $(y_{i_1}, y_{i_1+1}, …, y_{j_1})=[\mathrm{EndOfSlot}]$ 然后计算相关损失。当使用 Sequence Finalization 时,遇到 $l=0, 2$ 这种情况的时候,我们认为这里需要插入空字符串,跳过这两个位置的损失计算。直到所有的 slot 都不再产生损失(也就是所有 slot 都要插入空字符串)的时候,我们让每个 slot 都和 end-of-sequence token 计算损失。推理的时候,任意一个 slot 的预测是 end-of-sequence token 则停止解码。
4. Inference
4.1 Greedy Decoding
Greedy decoding 支持 Slot Finalization 和 Sequence Finalization 两种终止条件的训练模式。推理的时候选择概率最高的词和对应的位置:
然后再 $\hat{l}_t$ 位置上插入 $\hat{c}_t$。
4.2 Parallel Decoding
采用 Slot Finalization 方式支持并行训练和解码。具体来说,就是对于每个 slot 计算最高概率的词:
这样相当于每次推理我们能填满所有 slot,理论上,只需要 $\log_2(n)+1$ 步就可以生成一个长度为 $n$ 的序列。
5. Tricks
作者对模型做了非常充分的实验,也做了很多有意思的讨论。这里总结一些比较有用的小 tricks:
- 由于两种终止条件在训练的时候引入了过多的 $< EOS >$, 会导致模型在推理时很容易生成 $< EOS >$造成早停的问题。因此文章引入了 $< EOS >$ 惩罚来在推理时对 $< EOS >$ 人为地增加预测难度:仅当 $< EOS >$ 的概率大于第二可能单词的概率一个阈值 $\beta$ 的时候才会真正生成 $< EOS >$。从实验中看来,这是一个很重要的 trick。
- 使用base Transformer 作为模型的 teacher model,来做知识蒸馏也会提升模型的能力。
6. Experiments
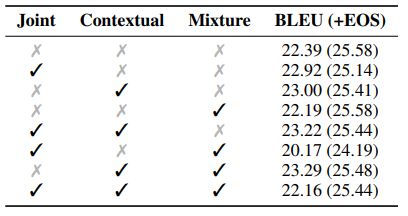
这个实验是分析 2.1 节讨论的模型的不同变种的效果。从结果上看,不加 $< EOS >$ 惩罚的时候,Contextual + Mixture 能达到最佳效果,但是加上惩罚之后这种效果提升就消失了。说明模型的核心结构在适当的调整下已经足够强大有效,无需做太大的调整。
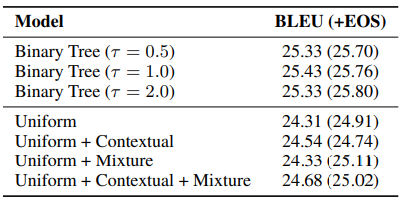
这个实验室采用并行解码的方式进行推理。我们发现之前介绍的平衡二叉树损失是非常有效的,另外$< EOS >$ 惩罚带来的提升已经不太明显了。
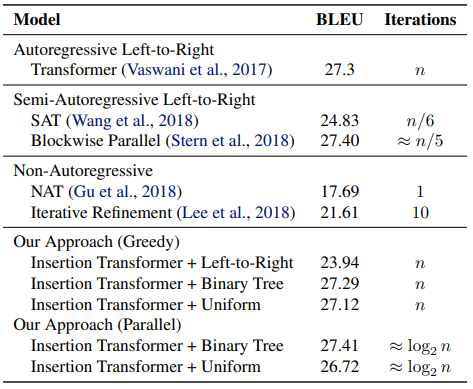
最后,与其他模型相比较,Insertion Transformer 不仅在效率上提升巨大,而且在效果上也达到了与自回归模型相同的水准。这是一个非常令人兴奋的结果。
最后,下面这张图展示了 Insertion Transformer 的一个实际推理的例子。

Reference
- Insertion Transformer: Flexible Sequence Generation via Insertion Operations, Mitchell Stern, William Chan, Jamie Kiros, Jakob Uszkoreit, 2019, arXiv: 1902.03249
- Breaking The Softmax Bottleneck: a High-Rank RNN Language Model, Zhilin Yang , Zihang Dai, Ruslan Salakhutdinov, William W. Cohen, 2018, arXiv: 1711.03953
- Insertion Transformer: Flexible Sequence Generation via Insertion Operations #123, kweonwooj, Github Pages
- Non-Autoregressive NMT: Insertion Transformer, Leo Guo, 知乎
- 香侬读 | 按什么套路生成?基于插入和删除的序列生成方法, 香侬科技, 知乎
- Understanding the Mixture of Softmaxes (MoS)



