Transformer家族之Sparse Transformer

目前来看，自注意力机制有一统NLP的趋势，其凭借能够捕捉序列中任意两个元素的关联信息，且易于并行等优势，在与传统的NLP武林盟主RNN的较量中，几乎是全方位碾压。但是它也并不是没有弱点，之前我们介绍过在机器翻译过程中，它的推理过程是auto-regression的，严重制约了它的推理效率。因此，很多研究人员对它做了一定程度上的改善。今天我们继续来对它进行其他方面的优化，也就是变形金刚家族的另一成员 —— Sparse Transformer。

在介绍 Sparse Transformer 之前我们要先思考一个问题：我们为什么要对它进行稀疏化改进？稀疏注意力能解决现有的什么问题？

1. Why you need Sparsity?

1.1 计算复杂度

从理论上来讲，Self Attention的计算时间和显存占用量都是$O(n^2)$级别的（$n$是序列长度），这就意味着如果序列长度变成原来的2倍，显存占用量就是原来的4倍，计算时间也是原来的4倍。现在，AI 研究中的一项挑战是对长序列的精细相关性建模，比如图像、声音等。如果我们在每一层都构建一个$n \times n$的注意力矩阵的话会消耗大量的内存。例如：

而目前用于深度学习的标准GPU显存是12-32G。因此全自注意力（full self-attention）严重制约了模型的编码长度。

1.2 注意力集中问题

理解自然语言需要注意最相关的信息。例如，在阅读过程中，人们倾向于把注意力集中在最相关的部分来寻找他们心中问题的答案。然而，如果不相关的片段对阅读理解产生负面影响，就会出现检索问题。这种分心会阻碍理解过程，而理解过程需要有效的注意力。比如：

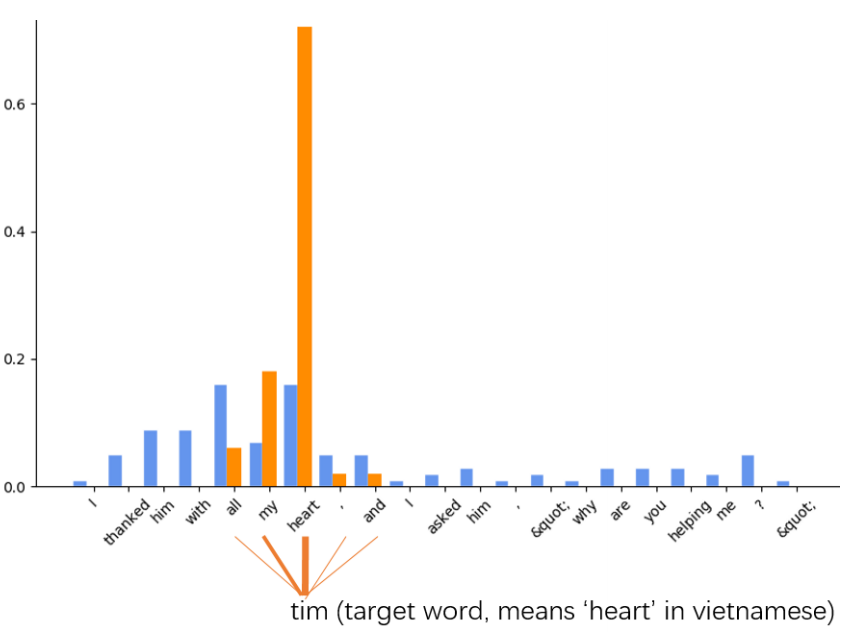
与tim相关度最高的是heart及周围的几个词，而传统的transformer也给了其他不相关的词很高的权重，这样造成了注意力的分散。Sparse Transformer可以将注意力集中在几个最重要的元素上，避免或者缓解这一问题。

2. Sparse Transformer

这里我们呢主要介绍四种Sparse Transformer :

• Sparse Transformers
• Adaptive Span Transformers
• Adaptively Sparse Transformers
• Explicit Sparse Transformer

2.1 注意力模式

既然要将注意力稀疏化，那么如何稀疏就是个需要思考的问题。为了更好的处理这个问题，Child等人在图像上探究了Transformer 的注意力模式发现其中许多模式表现出了可解释和结构化的稀疏模式。以下每幅图像都显示了哪个输入像素（白色高亮标出）由一个给定的注意力头处理，以预测图像中的下一个值。当输入部分集中在小的子集上并显示出高度规律性时，该层就易于稀疏化。以下是 CIFAR-10 图像上 128 层模型的样本：

左图是Layer 19的注意力模式（白色高亮），右图是Layer 20的注意力模式。可以看到Layer 19集中了当前行的注意力，Layer 20集中了当前列的注意力。

左图是Layer 6的注意力模式，右图是Layer 36的注意力模式。可以看到Layer 6无论输入是什么，注意力的集中点都具有相似的模式，Layer 36的注意力高度依赖具体的数据。

另外，Sukhbaatar等人也对比了两个Transformer注意力头的注意力模式：

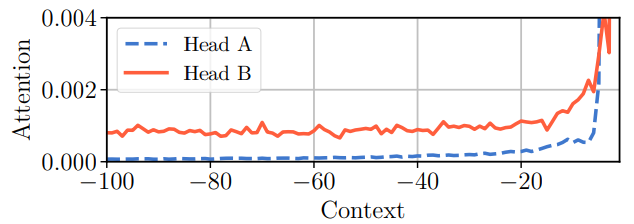
可以看到，Head A的注意力主要在最近的20个token，前面的80个token注意力权重很低，Head B的注意力主要集中在最近的20个token，但前80个token的注意力是均匀分布的。

从上面两个实验可以看出，注意力通常是稀疏的，而且在不同的层有不同的模式。虽然许多层显示出稀疏的结构，但有些层清晰地显示出了动态注意力，这种注意力延伸到整个图像。这个结论和我们在《Transformer的每一个编码层都学到了什么？》)中讨论的结果基本一致。

由于注意力机制的稀疏模式，研究人员提出了不同的稀疏化方法，下面我们介绍其中几种。

2.2 Sparse Transformers

2019年OpenAI研究人员研发出一种Sparse Transformers，该模型在预测长序列方面创造了新纪录——无论预测的是文本、图像还是声音，可以从长度可能是之前30倍的序列中提取模式。

对于图像这种具有周期性结构的数据来说，作者提出Strided Sparse Transformer。从上面的Layer 19和Layer 20可以看出注意力分为关注当前行和当前列。作者可以根据这两种注意力模式设计两个稀疏注意力矩阵。

2.2.1 Full Self Attention

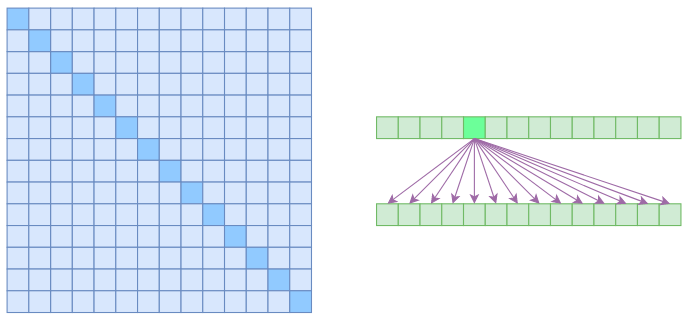
在上图中，左边显示了注意力矩阵，右变显示了关联性。这表明每个元素都跟序列内所有元素有关联。注意力稀疏化一个基本的思路就是减少关联性的计算，也就是认为每个元素只跟序列内的一部分元素相关，这就是稀疏注意力的基本原理。

2.2.2 Atrous Self Attention

首先考虑列性注意力。对于一张图片来说，我们如果把图片展开成一个一维序列，对于之前注意力只关注当前列实际上就意味着，在这个展开的长序列中，注意力的关注点是间隔的，不连续的。这样引入一个新概念——Atrous Self Attention：

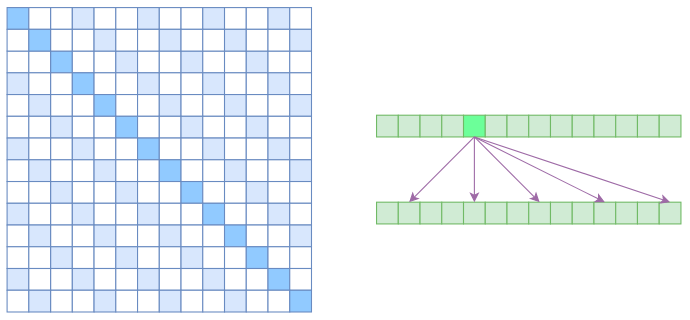
Atrous Self Attention 强行要求每个元素只跟它相对距离为$k,2k,3k,…$的元素关联，其中$k>1$是预先设定的超参数。由于现在计算注意力是“跳着”来了，所以实际上每个元素只跟大约$n/k$个元素算相关性，这样一来理想情况下运行效率和显存占用都变成了$O(n^2/k)$，也就是说能直接降低到原来的$1/k$。

2.2.3 Local Self Attention

再考虑行性注意力。当注意力只关注在一行的内容时相当于每个元素只与前后$k$个元素以及自身有关联，如下图：

其实Local Self Attention就跟普通卷积很像了，都是保留了一个$2k+1$大小的窗口，然后在窗口内进行一些运算，不同的是普通卷积是把窗口展平然后接一个全连接层得到输出，而现在是窗口内通过注意力来加权平均得到输出。对于Local Self Attention来说，每个元素只跟2k+12k+1个元素算相关性，这样一来理想情况下运行效率和显存占用都变成了$O((2k+1)n)∼O(kn)$了，也就是说随着$n$而线性增长，这是一个很理想的性质——当然也直接牺牲了长程关联性。

2.2.4 Stride Sparse Self Attention

到此，就可以很自然地引入OpenAI的Sparse Self Attention了。OpenAI将Atrous Self Attention和Local Self Attention合并为一个，形成适用于图像的Strided Sparse Transformer:

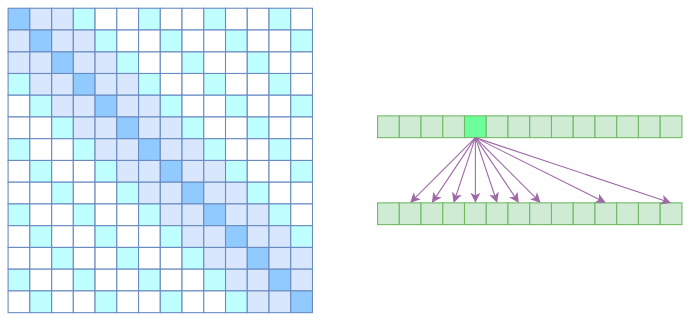
这样一来Attention就具有局部紧密相关和远程稀疏相关的特性，这对很多任务来说可能是一个不错的先验，因为真正需要密集的长程关联的任务事实上是很少的。

2.2.5 Fix Sparse Self Attention

对于文本这种非周期的数据，上面的Stride Sparse Transformer并不能很好的获取数据特征，作者认为是因为对于文本来说，元素的空间坐标和它所处的位置并没有必然的联系，它可能与未来的元素关联性更大，因此，作者提出另一种稀疏注意力模式——Fix Sparse Transformer。

Fix Sparse Transformer同样是由两个注意力机制合并组成的，一种如下图，相当于将完整序列划分成多个子序列，在每个子序列内部做full self attention。

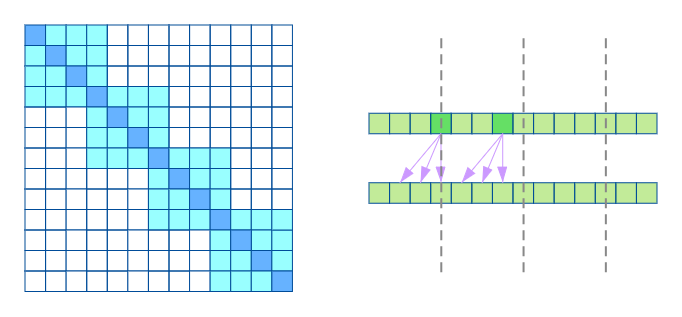
另一种如下图，相当于只计算序列上固定几个位置的元素计算注意力权重。

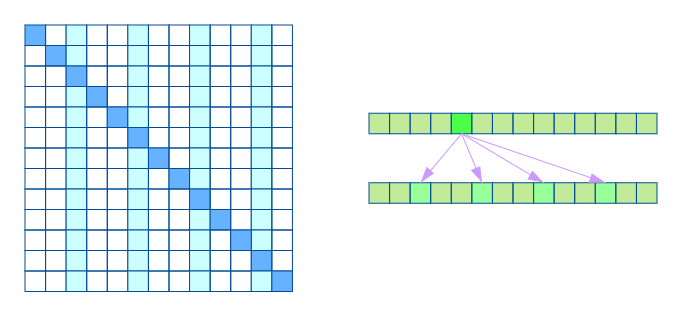
两种注意力相结合同样保证了局部紧密相关和远程稀疏相关特性。

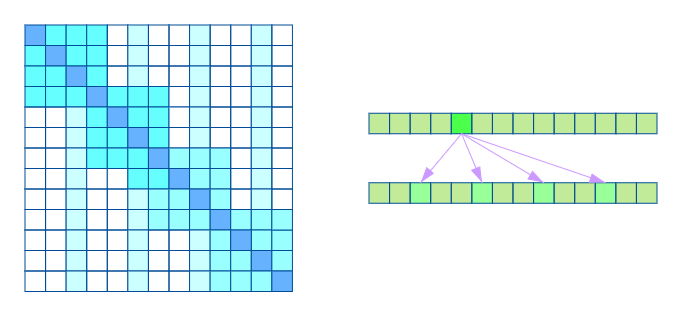
2.3 Adaptive Span Transformers

上面的稀疏化方法是研究人员利用先验知识，人工设计的一种稀疏化方法。这些方法可以很好的处理明显具有稀疏化特征的注意力机制，比如Layer 19/20，但是对于具有全局注意力和依赖数据特征的注意力机制，利用上述的稀疏化方法会影响最后的效果。因此，我们就想能不能设计一种自适应的注意力稀疏化机制，让模型自己决定要怎样稀疏化，这样可以避免人工设计的缺陷。

针对这个问题，Facebook的研究人员提出一种新的方法，利用一个$M_z$函数自动过滤一定长度的子序列，不参与注意力计算。$M_z$函数定义如下：

$$m_z(x)=\min[\max[\frac{1}{R}(R+z-x), 0], 1]$$

这个函数的大致形状如下：

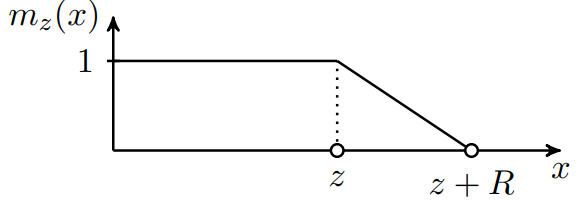
其中$R$是超参数，用来控制斜率。$z$是一个需要训练的参数，$x$是相对距离。得到这样一个函数以后，计算注意力的方法如下：

$$a = \frac{m_z(t-r)\exp(s_{tr})}{\sum_{q=t-s}^{t-1}m_z(t-q)\exp(s_{tq})}$$

在损失函数中，给z添加一个L1惩罚项：

$$L = -\log P(w_1,...w_T)+\frac{\lambda}{M} \sum_iz_i$$

另外，我们也可以用动态方式来学习$z$，即$z$是基于当前输入的一个输出，称之为动态宽度。

$$z_t = S\sigma(\mathbf{v}^T\mathbf{x}_t+b)$$

从上面的函数图可以看出来，

1. 当$z$大于两元素的相对距离时，最后的注意力相当于Full self attention;
2. 当$z$小于两元素的相对距离时，注意力会更集中在近距离元素上，相当于Local self attention；
3. 当$z$很小时，远距离的元素上不会有任何注意力

可以看出这样同样是既保留了局部的依赖，又处理了远程的稀疏性，而这样一个过程是模型自行决定，有效避免了人为设计的缺陷。

2.4 Adaptively Sparse Transformers

回想前面的稀疏化方法，我们发现之前的两种稀疏化方法都存在一个问题就是，注意力是连续性的。比如Adaptive Span Transformer，会忽略掉远距离的元素；虽然Sparse Transformer中包含了Atrous Attention，但是这种不连续性是人为设计的，具有固定的模式，不能很好的适应不同的数据。因此，本文提出一种新的方法，既能处理不连续的注意力，又能使这种不连续的注意力做到自适应不同的数据。

纵观我们从介绍注意力机制开始，到Transformer，再到后来的各种变种，有一个东西是自始至终都和注意力形影不离，那就是Softmax。Softmax是将一个向量进行归一化，将向量中每一个元素赋予概率的意义，而这个概率本身就是连续的。因此，如果要处理不连续性的注意力机制，我们是否可以将softmax进行稀疏化呢？

本文就引入一个新的Softmax函数，实现了注意力的不连续稀疏化——$\alpha$-$\rm{entmax}$：

$$\alpha - \mathrm{entmax}(\mathbf{z}) = \arg \max_{\mathbf{p} \in \Delta^d} \mathbf{p}^T\mathbf{z}+\mathbf{H}_\alpha^T(\mathbf{p})$$

其中$\Delta^d=\{\mathbf{p} \in \mathbb{R}^d:\sum_i\mathbf{p}_i=1\}$，对于$\alpha \ge 1$，$\mathrm{H}_\alpha^T$是Tsallis广延熵族：

$$\mathbf{H}_\alpha^T(\mathbf{p})=\begin{cases} \frac{1}{\alpha(\alpha-1)}\sum_j(p_j-p_j^\alpha), \alpha \ne 1, \\\\ \\\\ -\sum_jp_j\log p_j, \alpha =1. \end{cases}$$

可以看到，这样一个函数是非连续性的，面临一个凸优化的问题。实际上我们可以通过下面的公式对其进行优化：

$$\alpha-\mathrm{entmax}(\mathbf{z}) = \left[ (\alpha-1)\mathbf{z}-\tau\mathbf{1}\right]_+^{1/\alpha-1}$$

其中$\mathbf{1}$表示元素全为1的向量，$\tau$是一个拉格朗日乘子为了保证$\sum_ip_i=1$，$[\cdot]_+$表示$\mathrm{ReLU}$的正数部分。

看公式实在头疼，看不出为啥这样一个公式能将注意力进行稀疏化，那我们就来看图：

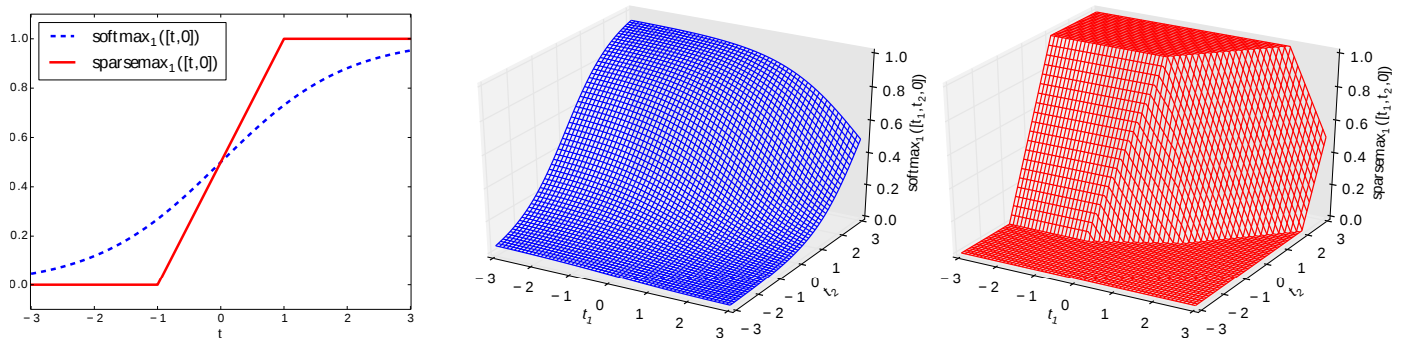
左边是二维图像，右边的两幅图分别是softmax和$\alpha=2$的$\alpha$-$\mathrm{entmax}$。可以看出当 $t$ 过小的时候，输出就会变成0；$t$ 过大的时候，输出就会变成1，这样也就相当于将注意力稀疏化了。

剩下的 工作就是为了确定 $\tau$，以及为了自适应不同的注意力头（transformer是多注意头的）的 $\alpha$ 值，作者将 $\alpha$ 作为网络的参数，利用后向传播进行优化等一系列细节，这里就不做详细介绍了。

本文涉及到的数学原理和公式的推导在引文和文章附录中都有详细推导，这里就不搬上来了，有兴趣可以自己看。

2.5 Explicit Sparse Transformer

Explicit Sparse Transformer虽然实现了不连续的自适应稀疏化自注意力，但是其实整个过程蛮复杂的，尤其是其中涉及到的数学，看了让人头秃（我边推公式边看着头发往下掉，内心毫无波动…）。有没有一种既简单易实现，又能做到不连续自适应的稀疏化自注意力呢？当然有咯，接下来就来介绍这样一个工作。

Explicit Sparse Transformer的想法非常简单：它认为在计算注意力的时候，只有注意力最高的$k$个词对信息的获取有作用，其他低注意力的属于噪声，非但不会帮助模型获取有效信息，还会干扰模型做出正确决策。因此，在计算自注意力的时候，每个词只取注意力权重最高的$k$个词，其他的全部设置成$-\infty$。计算过程如下：

1. 首先计算注意力矩阵$P$；
2. 找出 $P$ 中每行的 $k$ 个最大元素，记录其位置，并得到一个阈值向量，$t=[t_1, t_2, …, t_{lQ}]$，$t_i$ 表示第 $i$ 行中$k$ 个元素中注意力最低的那个值；
3. 得到一个$Masking$矩阵：

$$M(P, k)_{ij} = \begin{cases} P_{ij}, \qquad P_{ij} \ge t_i \\\\ \\\\ \mathrm{-} \infty, \qquad P_{ij} \lt t_i \end{cases}$$

1. 归一化

$$A = \mathrm{softmax} (M(P, k))$$

1. 输出表示

$$C = AV$$

整个流程如下：

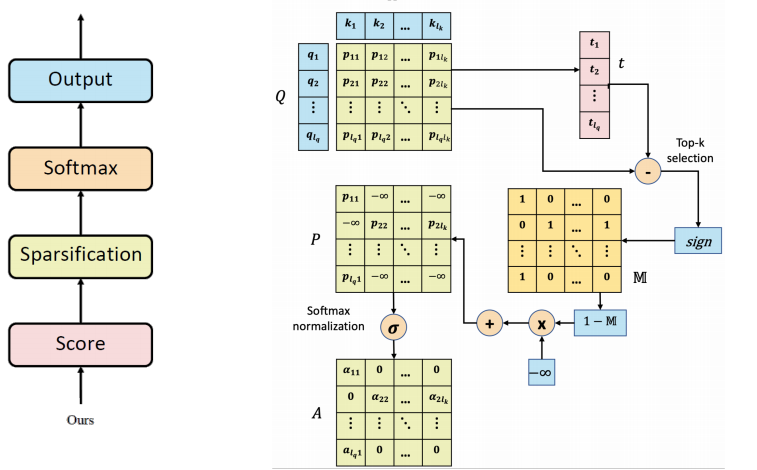
根据作者的实验表明，序列长度与vanilla transformer一致时，$k=8$能得到最佳结果。

关于取$\mathrm{top}-k$以后的后向传播问题，作者在论文的附录中给出了解释，有兴趣的可以看原文哟。

最后说几句吧，这个文章是投稿给了ICLR 2020，但是被拒稿了，拒稿的理由主要是效果没有达到SOTA，额，我觉得嘛，黑猫白猫，能抓老鼠就是好猫。

References

1. 为节约而生：从标准Attention到稀疏Attention，苏剑林， 科学空间
2. Generative Modeling with Sparse Transformers, Rewon Child, Scott Gray, Alec Radford, Ilya Sutskever, 2019, Arxiv:1904.10509
3. Generative Modeling with Sparse Transformers, OpenAI’s blog
4. EXPLICIT SPARSE TRANSFORMER: CONCENTRATED ATTENTION THROUGH EXPLICIT SELECTION, Guangxiang Zhao, Junyang Lin, Zhiyuan Zhang,Xuancheng Ren, Xu Sun, 2019, Arxiv:1912.11637
5. Adaptive Attention Span in Transformers, Sainbayar Sukhbaatar, Edouard Grave, Piotr Bojanowski, Armand Joulin, 2019，Arxiv:1905.07799
6. Transformer之自适应宽度注意力, 张雨石， 知乎
7. Adaptively Sparse Transformers, Goncalo M. Correia， Vlad Niculae，Andre F.T. Martins，2019，Arxiv:1909.00015