Rogerspy's Home

Transformer家族之Weighted Transformer

Rogerspy

2019-09-19

NLP

字数统计: 2.3k字   |   阅读时长≈ 10分

之前我们介绍了擎天柱的工作原理以及内部构造。对擎天柱已经有了深入的了解，那么本文就来介绍一下汽车人家族中的其他成员——Transformer的各种变种。

1. Weighted Transformer

1. Weighted Transformer

为了更快的训练和更好的发挥Transformer的信息表示能力，Ahmed et al. 2017提出了这种新的结构。

1.1 模型结构

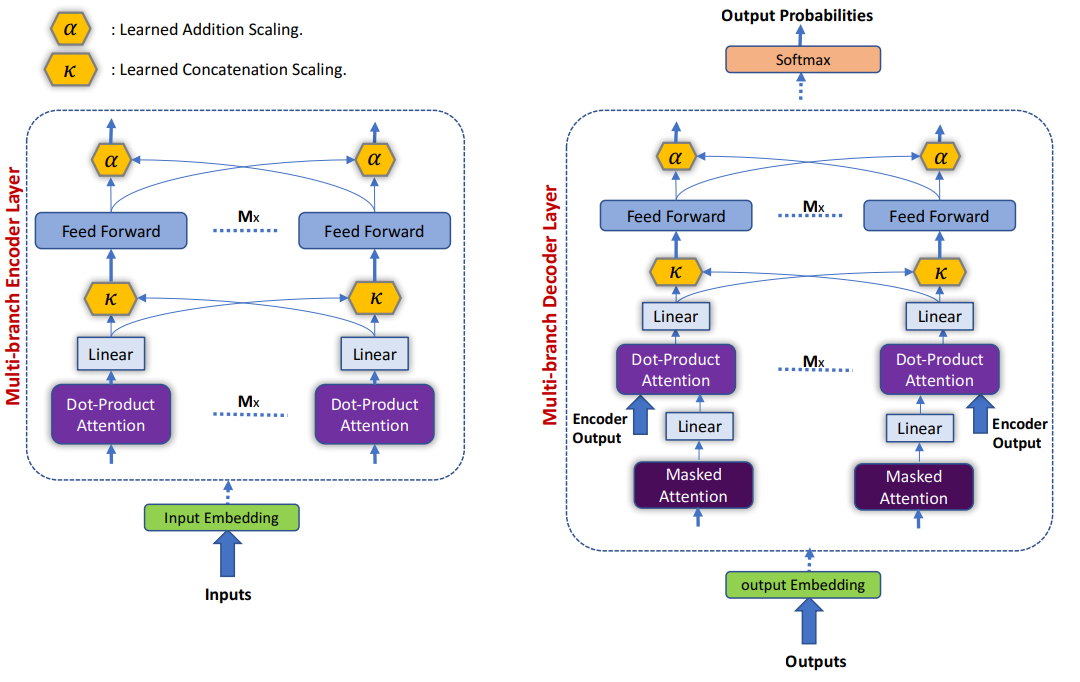
模型在整体结构上和Transformer差不多，不同点有两个：

  • 使用Multi-branch代替Multi-Head；
  • 在FFN上不是直接线性转换，而是Multi-branch线性转换后加权求和。

公式如下：

1.2 Multi-branch Attention

在Weighted Transformer中对Attention的计算和标准的Transformer计算过程是一致的，所以这里不做介绍。接下来对计算完的scaled dot-product attention的处理上，模型就在原始Transformer上做了修改。作为对比，我们把原始的Transformer在这一步的处理也列出来：

Transformer是直接将heads进行线性变换，而Weighted transformer在对每个head进行线性变换后还乘上一个$\kappa$参数，这个参数是可训练的，而且必须满足条件：$\sum_i \kappa_i =1$。这个参数作者称之为concatenation weight。

我们知道Multi-head中的每一个head的作用是学习句子的不同信息，Transformer认为每个head学到的信息对任务来说是平权的，因此直接将多个head直接等权拼接，然后线性变换。而Weighted transformer认为每个head对任务的作用是不同的，因此为每个head分配一个权重，用于表明这个head对任务的重要性，而权重的大小令模型自动从任务中学习。这种假设显然应该比Transformer的平权假设要更加合理。

1.3 Weighted point wise feed forward network

这一部分我认为作者要么是对Transformer的理解有误，要么是论文的表述不准确，在对比Transformer和Weighted Transformer的时候有点小冲突，比如作者说Transformer对应的FFN公式是$BranchedAttention(Q, K, V)=\mathrm{FFN}(\sum_i^M \overline{head_i})$，先不纠结BranchedAttention的函数名问题，作者认为每个head是通过求和， 然后再经过FFN。但是Transformer原始论文写的很清楚head是通过Concat拼接在一起的，并非求和。造成作者在这里使用$\sum_i^M\overline{head_i}$，我个人猜测有两个可能的原因：

1. 作者使用$\sum$的意图其实是Concat

2.作者可能把Transformer结构图中Add当成了对head求和

无论什么原因，下面的介绍我都会替换成Concat。另外，作者介绍Weighted transformer的FFN的时候使用的也是$\sum$，但是从作者在其他的地方的表述来看，这里的求和应该指的也是Concat。比如作者将$\kappa$命名为concatenation weight，另外作者认为weighted transformer的参数只比transformer多了$\alpha$和$\kappa $，所以总的参数量应该是相同的，但是如果在weighted transformer中这一步使用了求和的话，假设$h=8, d_k=d_v=64$， 那么FFN的输出维度应该是（batch_size, seq_len, 64），而Transformer的输出维度是（batch_size, seq_len, 512），这样参数量是不同的， 除非在weighted transformer中作者令$d_k=d_v=512$，但是如果是这样的话，每个head的参数又不同了，所以无论如何weighted trnasformer和transformer的参数都是不同的。因此，我认为这里应该是Concat。

刚开始的时候由于思考的不周全，以为是作者在论文中的表述不准确，所以自己瞎讨论半天，后来发现作者的表述没有任何问题，而是自己的问题，所以上面的内容只保留删除线，不把内容删除，用来提醒自己曾经犯过的错误。

这里解释一下为什么作者表述是正确的，而我的理解是错误的呢？首先说作者在描述transformer的时候用的公式$BranchedAttention(Q, K, V)=\mathrm{FFN}(\sum_i^M \overline{head_i})$，我之前认为原始论文中这里应该是Concat而不应该是$\sum$，但是我忽略了一点，就是在transformer原始论文中，是先进行Concat，这个时候输出tensor.shape == (batch_size, seq_len, d_model)，再进行线性变换的时候$W^{O_i}$的形状应该是（d_model, d_model），所以FFN的输出是(batch_size, seq_len, d_model)。但是本文中是先进行的线性变换，我原先想的是线性变换的tensor.shape == (batch_size, seq_len, d_v)，而$W^{Q_i}.shape == (d_v, d_v)$，这样得到的输出形状是(batch_size, seq_len, d_v)，然后平权求和，如果是这样的话就会出现我上面的错误，缺少Concat和输出维数对应不上的问题。但实际上这里的$W^{Q_i}.shape == (d_v, d_{model})$，这样会输出$M$个形状为(batch_size, seq_len, d_model)的tensor（这就是$\overline{head_i}=head_iW^{O_i}$这一步做的事情），然后通过沿着head方向求和就可以得到一个形状为(batch_size, seq_len, d_model)的tensor（这就是$\mathrm{FFN}(\sum \overline{head_i})$这一步做的事情），实际上本文作者的操作和transformer的原始论文的操作是等效的。我的思考主要问题出现在了线性变换这一步的输出上。下面我们继续跟随作者的脚步，看下他在FFN上做了什么文章。

Transformer在计算FFN的过程如下：

可以看到两者的区别仍然是对不同head信息的加权方式不同，transformer仍然认为是平权的，但是weighted transformer认为是各有不同的权重，和$\kappa$一样，$\alpha$是从任务中学习的，且满足$\sum_i\alpha_i=1$。作者给$\alpha$取了一个名字叫做addition weight。

2. 模型细节

除了以上两点修改以外，其他方面没有做任何修改。但是在训练的时候$\alpha$和$\kappa$的学习率由下式确定：

也就是说将warmup_steps改成400。

3. 代码实现

3.1 pytorch核心代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
class MultiBranchAttention(nn.Module):
    def __init__(self, depth, d_model, d_ff, n_branches, dropout):
        super(MultiBranchAttention, self).__init__()
        self.depth = depth
        self.d_model = d_model
        self.d_ff = d_ff
        self.n_branches = n_branches
        # in practice, d_model == d_k * n_branches
        assert d_model == d_k * n_branches
        
        # Q, K, V Linear
        self.w_q = Linear([d_model, d_model])
        self.w_k = Linear([d_model, d_model])
        self.w_v = Linear([d_model, d_model])

        # scaled dot-product attention
        self.attentions = nn.ModuleList([
            # custom define
            ScaledDotProductAttention(depth, dropout) for _ in range(n_branches)
        ])
        
        # additional parameters for BranchedAttention
        # custom define
        self.w_o = nn.ModuleList([Linear(depth, d_model) for _ in range(n_branches)])
        self.w_kp = torch.rand(n_branches)
        self.w_kp = nn.Parameter(self.w_kp/self.w_kp.sum())
        self.w_a = torch.rand(n_branches)
        self.w_a = nn.Parameter(self.w_a/self.w_a.sum())

        # Position wise feed forward network
        self.ffn = nn.ModuleList([
            # custom define
            PositionwiseFeedForwardNetwork(d_model, d_ff//n_branches, dropout) 
            for _ in range(n_branches)])
        self.dropout = nn.Dropout(dropout)
        # layer normalization
        # custom define
        self.layer_norm = LayerNormalization(d_model)

        init.xavier_normal(self.w_o)

    def forward(self, q, k, v, attn_mask):
        # q: (batch_size, len_q, d_model)
        # k: (batch_size, len_k, d_model)
        # v: (batch_size, len_v, d_model) note (len_k == len_v)
        residual = q

        # Linear
        Q = self.w_q(q)  # (batch_size, len_q, d_model)
        K = self.w_k(k)  # (batch_size, len_q, d_model)
        V = self.w_v(v)  # (batch_size, len_q, d_model)
        
        # split
        Qs = Q.split(self.depth, dim=-1)  # (b_size, len_q, depth) x n_branches
        Ks = K.split(self.depth, dim=-1)  # (b_size, len_k, depth) x n_branches
        Vs = V.split(self.depth, dim=-1)  # (b_size, len_v, depth) x n_branches
        
        # scaled dot product attention
        # scaled_attn: (batch_size, len_q, d_v) x n_branch
        scaled_attn = [
            attn(Qs[i], Ks[i], Vs[i], mask) for i, attn in enumerate(self.attentions)
        ]
        
        # multi-branch attention
        # outputs: (b_size, len_q, d_model) x n_branches 
        outputs = [self.w_o[i](scaled_attn[i]) for i in range(self.n_branches)]
        outputs = [kappa * output for kappa, output in zip(self.w_kp, outputs)]
        # FFN
        outputs = [ffn(output) for ffn, output in zip(self.ffn, outputs)]
        outputs = [alpha * output for alpha, output in zip(self.w_a, outputs)]

        # output: (b_size, len_q, d_model)
        output = self.dropout(torch.stack(outputs).sum(dim=0))
        return self.layer_norm(residual + output)

3.2 tensorflow核心代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class MultiBranchAttention(tf.keras.layers.Layer):
    """
    Implement Multi-branch attention layer.
    """
    def __init__(self, depth, d_model, d_ff, n_branches, dropout):
        super(MultiBranchAttention, self).__init__()
        
        self.depth = depth
        self.d_model= d_model
        self.d_ff = d_ff
        self.n_branches = n_branches
        self.dropout = dropout
        
        # K, Q, V, linear
        self.wq = tf.keras.layers.Dense(d_model)
        self.wk = tf.keras.layers.Dense(d_model)
        self.wv = tf.keras.layers.Dense(d_model)
        
        # scaled dot product attention
        self.attentions = [
            # custom define
            scaled_dot_product_attention(depth, dropout) for _ in range(n_branches)
        ]
        
        # additional parameters for BranchedAttention
        self.w_o = [tf.keras.layers.Dense(d_model) for _ in range(n_branches)]
        self.w_kp = np.random.random((n_branches,))
        self.w_kp = tf.Variable(self.w_kp/self.w_kp.sum(), trainable)
        self.w_a = np.random.random((n_branches,))
        self.w_a = tf.Variable(self.w_a/self.w_a.sum(), trainable)

        # Position wise feed forward network
        self.ffn = [
            # custom define
            PositionwiseFeedForwardNetwork(d_model, d_ff//n_branches, dropout) 
            for _ in range(n_branches)]
        self.dropout = tf.keras.layers.Dropout(dropout)
        # layer normalization
        self.layer_norm = tf.keras.layers.LayerNormalization(epsilon=1e-6)
        
        self.dense = tf.keras.layers.Dense(d_model)
    
    def call(self, q, k, v, mask):
        residual = q
        
        # First linear transition step
        Q = self.wq(q)  # (batch_size, seq_len, d_model)
        K = self.wk(k)  # (batch_size, seq_len, d_model)
        V = self.wv(v)  # (batch_size, seq_len, d_model
        
        # Split K, Q, V into multi-branch
        Qs = tf.split(Q, n_branches, axes=-1)  # (batch_size, len_q, depth) x n_branches
        Ks = tf.split(K, n_branches, axes=-1)  # (batch_size, len_k, depth) x n_branches
        Vs = tf.split(V, n_branches, axes=-1)  # (batch_size, len_v, depth) x n_branches
        
        # Scaled Dot-Product Attention step
        # head_i = Atteniton(QW_Q, KW_K, VW_V)
        scaled_attention = [
            attn(Qs[i], Ks[i], Vs[i], mask) for i, attn in enumerate(self.attentions)
        ]
        # scaled_attention.shape == (batch_size, len_q, depth)
        
        # multi-branch attention
        # outputs: (b_size, len_q, d_model) x n_branches 
        outputs = [self.w_o[i](scaled_attention[i]) for i in range(self.n_branches)]
        outputs = [kappa * output for kappa, output in zip(self.w_kp, outputs)]
        # FFN
        outputs = [ffn(output) for ffn, output in zip(self.ffn, outputs)]
        outputs = [alpha * output for alpha, output in zip(self.w_a, outputs)]

        # output: (b_size, len_q, d_model)
        output = self.dropout(tf.stack(outputs).sum(dim=0))
        return self.layer_norm(residual + output)

4. 参考资料

  1. Weighted Transformer Network for Machine Translation, Ahmed et al., arxiv 2017
 上一页

Transformer NMT

 评论