Rogerspy's Home

关于Transformer的分析

Rogerspy

2019-09-01

NLP

字数统计: 10.9k字   |   阅读时长≈ 44分

Transformer 的模型框架我们已经介绍完了，接下来这篇文章我们讨论一下更多关于 Transformer 的模型细节。比如多头注意力的头越多越好吗？自注意力为什么要进行归一化？训练的时候 Warm-up 有什么用？

1. 模型总览

在进入正题之前，我们先回顾一下 Transformer 的整体结构，大致包含以下几个部分：

  • Input Embedding
  • Positional Encoding
  • Multi-head Attention
  • Add & Norm
  • Feed Forward
  • Masked Multi-head Attention
  • Linear
  • softmax

2. Input Embedding

Input Embedding 实际上可以看成两部分：Input 和 Embedding。神经网络在处理自然语言问题的时候，一个基础的工作就是词向量化。要将自然语言问题转化成计算问题，首先就要将自然语言符号表示转化成数字表示，最简单的表示方法就是 one-hot ，但是 one-hot 有两个问题：① 数据稀疏；② 无法表示词语此之间的语义关系。所以后来人们发明了 embedding 表示法，就是将自然语言符号表示成低维连续的向量，这样可以同时解决上述两个问题。

向量化是自然语言处理的一个必不可少的工作，一般的词向量化有两种方式：

  • 通过一些算法（比如，word2vec 或者 glov2vec）预训练一个词向量表，之后通过查表的方式将句子转化成词向量表示。然后在模型的训练的时候词向量不参与训练；
  • 在模型输入阶段随机初始化一张词向量表，同样是通过查表的方式将句子表示成向量形式，而这张词向量表随着模型一起训练。

以上基本就是任意使用神经网络处理的自然语言问题的必经之路。其中的向量化过程我们不再赘述（在后续的系列文章中会专门讨论自然语言处理中的预训练技术），这里我们详细讨论一下 Input 部分。

上面我们说到我们需要一张词向量表将自然语言符号映射成向量，自然而然地我们同样需要一张词表，这张词表包含的元素就是自然语言符号。在训练模型的时候我们是使用一张固定大小的词表，也就是说模型只能处理词表中出现过的词。一个显然的问题是，大千世界，我们人类发明的自然语言符号虽然不是无穷无尽的，但是却是数量非常庞大的，而且还在不断的增长中，所以我们不可能将所有的符号都纳入到词表中。即使我们将当前所有的符号都纳入到词表中也会面临两个问题：

  • 过于庞大的词表就意味着庞大的词向量表，如此庞大的词向量表会使模型参数量爆炸，大参数量不仅意味着大计算量，同时还有可能意味着较高的错误率。比如机器翻译过程中最后的输出由 softmax 挑选最合适的词进行输出，一个简单的直觉就是从更大的词表中选择会有更大的概率出错；
  • 在所有的符号中，有些是常用的，有些是非常罕见的。对于常用的符号，模型可以得到充分的训练，但对于稀有的符号模型得不到充分训练，实际的效果也不会好。

这就意味着我们的模型只能使用一个有限的词表进行训练，但是当我们的模型训练好了以后，让它去处理实际问题的时候，它面临的却是开放的世界，它需要处理的也是所有的自然语言符号，一旦遇到词表之外的符号，模型就无能为力了。这就是自然语言处理过程中的 OOV（out-of-vocabulary） 问题。

为了解决 OOV 问题，研究人员展开了大量的研究工作，研究的核心就在于以什么样的方式表示自然语言符号。

  • 以词为单位。通常，我们认为一个句子的基本元素是词（word），所以我们通常是使用一个个词组成一个序列，用来表示句子。而使用词作为自然语言符号表示法的话，就会面临上述的所有问题。而且以词为单位不利于模型学习词缀之间的关系，比如模型学到的“old”, “older”, and “oldest”之间的关系无法泛化到“smart”, “smarter”, and “smartest”。
  • 以字为单位。后来人们想到用字（character）来表示。虽然真实世界的词浩如烟海，但是组成词的字却是非常有限的，比如英文只有 26 个字母。但是这种处理方法粒度太细，丢失了词带给句子的潜藏语义关联，因此通常效果不如以词为基础单元的模型。
  • 以子词为单位。什么是子词（sub-word）？就是将一般的词，比如 older 分解成更小单元，old+er，这样这些小单元可以几个词共用，减小了词表大小，同时还能使模型学习到词缀之间的关系。因此子词可以很好的平衡 OOV 问题。所以下面我们详细介绍一下子词技术。

2.1 Byte Pair Encoding

Byte Pair Encoding（BPE） 算法最早是由 Gage 于1994 年提出的一种用于数据压缩的算法，而在 2015 年被 Sennrich 等人推广到了自然语言处理领域。

  • 算法过程

算法过程如下：

1
2
3
4
5
6
1. 准备足够大的训练语料;
2. 确定期望的子词表大小；
3. 将单词拆分为字符序列并在末尾添加后缀“</w>”，统计单词频率；
4. 统计每一个连续字节对的出现频率；
5. 选择最高频者合并成新的子词；
6. 重复 4 ~ 5 步直到达到第2步设定的子词表大小或下一个最高频的字节对出现频率为 1。

举个例子：

  • 假设我们准备了一份语料，语料中包含：$(low, lower, newest, widest)$ 这几个词;

  • 将单词拆分成字符，并在后面添加 “</w>”，然后统计词频，得到：

    vocab = {‘l o w </w>’: 5, ‘l o w e r </w>’: 2, ‘n e w e s t </w>’: 6, ‘w i d e s t </w>’: 3}

  • 统计连续字符对出现的频率：

    {(‘l’, ‘o’): 7, (‘o’, ‘w’): 7, (‘w’, ‘</w>’): 5, (‘w’, ‘e’): 8, (‘e’, ‘r’): 2, (‘r’, ‘</w>’): 2, (‘n’, ‘e’): 6, (‘e’, ‘w’): 6, (‘e’, ‘s’): 9, (‘s’, ‘t’): 9, (‘t’, ‘</w>’): 9, (‘w’, ‘i’): 3, (‘i’, ‘d’): 3, (‘d’, ‘e’): 3}

  • 最高频连续字节对 (“e”, “s”)，合并成 “es”，得到：

    {‘l o w </w>’: 5, ‘l o w e r </w>’: 2, ‘n e w es t </w>’: 6, ‘w i d es t </w>’: 3}

  • 重复以上步骤

注意：停止符”</w>”的意义在于表示subword是词后缀。举例来说：”st”字词不加”</w>”可以出现在词首如”st ar”，加了”</w>”表明改字词位于词尾，如”wide st</w>”，二者意义截然不同。

  • 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import re, collections

def get_stats(vocab):
    pairs = collections.defaultdict(int)
    for word, freq in vocab.items():
        symbols = word.split()
        for i in range(len(symbols)-1):
            pairs[symbols[i],symbols[i+1]] += freq
    return pairs

def merge_vocab(pair, v_in):
    v_out = {}
    bigram = re.escape(' '.join(pair))
    p = re.compile(r'(?<!\S)' + bigram + r'(?!\S)')
    for word in v_in:
        w_out = p.sub(''.join(pair), word)
        v_out[w_out] = v_in[word]
    return v_out

训练示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vocab = {'l o w </w>': 5, 
         'l o w e r </w>': 2, 
         'n e w e s t </w>': 6, 
         'w i d e s t </w>': 3}
num_merges = 1000
for i in range(num_merges):
    pairs = get_stats(vocab)
    if not pairs:
        break
    best = max(pairs, key=pairs.get)
    vocab = merge_vocab(best, vocab)
    print(best)
    print(vocab)
    print('='*20)

输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
('e', 's')
{'l o w </w>': 5, 'l o w e r </w>': 2, 'n e w es t </w>': 6, 'w i d es t </w>': 3}
====================
('es', 't')
{'l o w </w>': 5, 'l o w e r </w>': 2, 'n e w est </w>': 6, 'w i d est </w>': 3}
====================
('est', '</w>')
{'l o w </w>': 5, 'l o w e r </w>': 2, 'n e w est</w>': 6, 'w i d est</w>': 3}
====================
('l', 'o')
{'lo w </w>': 5, 'lo w e r </w>': 2, 'n e w est</w>': 6, 'w i d est</w>': 3}
====================
('lo', 'w')
{'low </w>': 5, 'low e r </w>': 2, 'n e w est</w>': 6, 'w i d est</w>': 3}
====================
('n', 'e')
{'low </w>': 5, 'low e r </w>': 2, 'ne w est</w>': 6, 'w i d est</w>': 3}
====================
('ne', 'w')
{'low </w>': 5, 'low e r </w>': 2, 'new est</w>': 6, 'w i d est</w>': 3}
====================
('new', 'est</w>')
{'low </w>': 5, 'low e r </w>': 2, 'newest</w>': 6, 'w i d est</w>': 3}
====================
('low', '</w>')
{'low</w>': 5, 'low e r </w>': 2, 'newest</w>': 6, 'w i d est</w>': 3}
====================
('w', 'i')
{'low</w>': 5, 'low e r </w>': 2, 'newest</w>': 6, 'wi d est</w>': 3}
====================
('wi', 'd')
{'low</w>': 5, 'low e r </w>': 2, 'newest</w>': 6, 'wid est</w>': 3}
====================
('wid', 'est</w>')
{'low</w>': 5, 'low e r </w>': 2, 'newest</w>': 6, 'widest</w>': 3}
====================
('low', 'e')
{'low</w>': 5, 'lowe r </w>': 2, 'newest</w>': 6, 'widest</w>': 3}
====================
('lowe', 'r')
{'low</w>': 5, 'lower </w>': 2, 'newest</w>': 6, 'widest</w>': 3}
====================
('lower', '</w>')
{'low</w>': 5, 'lower</w>': 2, 'newest</w>': 6, 'widest</w>': 3}
====================

2.2 WordPiece

WordPiece 算法可以看作是 BPE 的变种。不同点在于，WordPiece 基于概率生成新的子词而不是最高频字节对。

  • 算法过程
1
2
3
4
5
6
1. 准备足够大的训练语料;
2. 确定期望的子词表大小;
3. 将单词拆分成字符序列;
4. 基于第3步数据训练语言模型;
5. 从所有可能的子词单元中选择加入语言模型后能最大程度地增加训练数据概率的单元作为新的单元;
6. 重复第5步直到达到第2步设定的子词表大小或概率增量低于某一阈值;

注意：因为加入每个可能的词对都需重新训练语言模型，这样需要的计算资源会很大，因此作者通过以下策略降低计算量：

  1. 只测试语料中出现的词对；
  2. 只测试有很大可能（高优先）是最好词对的候选；
  3. 同时测试几个词对，只要它们互不影响；
  4. 重训语言模型（并不需要是神经网络型），只重新计算受影响的部分。

2.3 Unigram Language Model

ULM 是另外一种子词分隔算法，它能够输出带概率的多个子词分段。它引入了一个假设：所有子词的出现都是独立的，并且子词序列由子词出现概率的乘积产生。

ULM 和 WordPiece 一样都是利用语言模型建立子词表。与前两者都不相同的是，前两者构建词表的时候是增量的，而 ULM 是减量的。

  • 算法过程
1
2
3
4
5
6
7
1. 先建立一个足够大的种子词表，可以用所有字符的组合加上语料中常见的子字符串。
   对于种子词表，也能用 BPE 法来生成。
2. 固定词表，用 EM 算法来最优化当前词表在语料上的概率；
3. 之后计算每个子词的 loss，对应的 loss 相当于该子词有多大可能使总的 loss 降低；
4. 接着按照每个子词 loss 大小来排序，保留最大一定比例（比如说80%）的子词，
   为了避免OOV，建议保留字符级的单元；
6. 不断重复 2 ~ 4，直到词表量减少到限定范围。
  • 子词采样

相比于之前的两种方法，分词结果是确定的，ULM 会使用一定的概率对分词结果进行采样。这样给训练过程带来了随机性。结果表明相比起只用一种方案的确定性分词法，子词正则能够获得很大的提升。但同时也正如看到的，子词正则加上 ULM 法过于复杂，所以应用难度也相应增大，不像 BPE 应用广泛。

2.4 BPE-Dropout

该方法非常简单，采取和子词正则相同思路，对 BPE 算法训练做了些改进，加入了一定的随机性。具体在每次对训练数据进行处理分词时，设定一定概率（10%）让一些融合不通过，于是即使是相同词，每次用 BPE dropout 生成出来的子词也都不一样。

  • 算法过程
1
2
1. 用 BPE 生成所有的融合候选子词；
2. 根据一定的概率 p 删除一部分候选子词；

2.5 小结

  1. 子词可以平衡词汇量和对未知词的覆盖。
  2. 对于包括中文在内的许多亚洲语言，单词不能用空格分隔。 因此，初始词汇量需要比英语大很多。
  3. 另外需要注意一点的是，对于中文这种不以空格分隔的语言，在应用子词技术的时候，需要先用分词算法进行分词。

3. Positional Encoding

3.1 What, why and when？

所谓位置编码指的是，在训练深度模型的时候，在输入训练数据的时候添加一种编码，使得模型的输出可以表征输入数据的时序特征。对于文本数据，词与词之间的顺序关系往往影响整个句子的含义。因此，在对文本进行建模的时候，词序是一个必须考虑的问题。但是否是所有的文本建模都需要使用位置编码呢？

答案是：No!

只有当我们使用对位置不敏感（position-insensitive）的模型对文本数据建模的时候，才需要额外使用位置编码。那么什么是位置敏感模型？什么是位置不敏感模型呢？

如果模型的输出会随着输入文本数据顺序的变化而变化，那么这个模型就是关于位置敏感的，反之则是位置不敏感的。

用形式化的语言描述为：假设模型函数 $y = f(x)$，其中 $x = (x_1, …, x_n)$ 为输入序列，$y$ 为输出。如果将 $x$ 找那个任意元素的位置进行了置换， $x’ = (x_{k_1}, …x_{k_n})$。此时，如果 $f(x) = f(x’)$，那么我们称模型是位置不敏感的；反之则为位置敏感的。

传统的 RNN 模型是关于位置敏感的模型，我们在使用 RNN 相关模型进行文本建模的时候是不需要位置编码的。只有使用位置不敏感的模型进行文本建模的时候才需要位置编码。

3.2 How?

从直观上来讲，我们可以给序列中的第一个词的位置编码为 1，第二个词位置编码为 2 …… 依此类推。但是这种方法会带来两个问题：① 句子比较长的话，位置编码数字会变得很大；② 模型在推理的时候会遇到比训练数据更长的句子，这种编码会削弱模型的泛化性。

我们直接能想到的第二种方法是，将序列长度归一化到 $[0, 1]$ 范围内，0 表示第一个词， 1 表示最后一个词。但是这种编码方式也是有问题的：句子是变长的，我们不知道模型遇到的句子的长度是多少，对于不同长度的句子，每个词对应的位置编码是不一样的，也就是说这样的位置编码是无效编码。举个例子：

I love you

I love you!

这两句话，实际上意思相同，只不过第二句话多了一个句号，在用上面的方式进行位置编码的时候，两句话中对应的词的位置编码是不一样的，最后模型输出的结果也很难表征出相同的意思。因此，这种方式同样不可取。

理想的位置编码应该具备以下几个特征：

  • 每一个词的位置都有一个唯一的编码；
  • 不同长度的句子中任意两个词之间的距离应该是相同的；
  • 编码值应该是有界的，而且可以轻松泛化到更长的句子中；
  • 必须具有确定性。

目前主流的位置编码有三种：

  1. 可学习的位置编码（Learned Positional Embedding）；
  2. 正余弦位置编码（Sinusoidal Position Encoding）；
  3. 相对位置编码（Relative Position Representations）。

3.2.1 可学习的位置编码

这种编码方式相对简单也容易理解。它的做法是，随机初始化一个位置矩阵，然后加到（或者拼接）词向量矩阵上，输入给模型作为模型参数参与模型训练。

3.2.2 正弦位置编码

这种位置编码方式就是 Transformer 中使用的位置编码。假设 $t$ 是输入序列的位置，$\vec{p}_t \in \mathbb{R}^d$ 表示其对应的编码。$\vec{p}_t$ 定义如下：

其中 $\omega_k = 1/10000^{2k/d}$。

有了位置编码以后，将词向量与位置向量相加得到带有位置信息的新序列。注意为了相加操作的正确，要保证此项来那个维度和位置向量维度一致：

正弦位置编码的优势是，对于任意固定的偏移量 $k$，$\vec{p}_{t+k}$ 可以表示成 $\vec{p }_t$ 的线性函数。也就是说，模型可以很容易通过先验绝对位置编码学习到相对位置编码。通常对于句子中的词序，我们更关注的是词与词之间的相对位置。我们来证明一下吧。

  • 问题描述

    令 $ \vec{p}_t$ 表示第 $t$ 个位置的位置编码：

    我们希望能找到一个与 $t$ 无关的矩阵，使得 $\vec{p}_t$ 通过线性变换成为 $\vec{p}_{t+k}$。（因为如果是关于 $t$ 的矩阵， 那这个变换就是非线性的了）

  • 证明

    我们令

我们希望找到一个 $M \in \mathbb{R}^{2 \times 2}$ ，使得

令 $M = \begin{bmatrix}u_1 & v_1 \\\ u_2 & v_2\end{bmatrix}$，代入上式，并分解等式右边得

由此可得：

通过对比等式两边，我们可以得到 $u_1, v_1, u_2, v_2$ 的一组解：

也就是说

我们可以看到 $M$ 是一个与 $t$ 无关的矩阵。最后，我们令

其中 $0$ 表示 $2 \times 2$ 的全零矩阵。$T^{(k)}$ 即为我们想要的线性变换矩阵。

  • 正弦位置编码的性质

    在计算自注意力的时候， Transformer 是计算序列中任意两个元素的注意力权重。因此，我们这里探究一下正弦位置编码的内积的性质。

    ① 内积随相对位置递增而减小

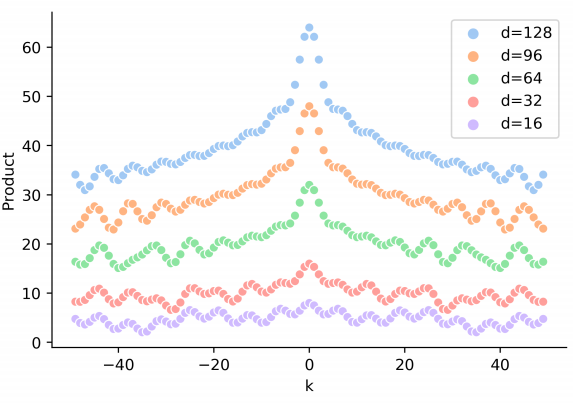
    由此我们可以发现，随着相对位置的递增，正弦位置编码的内积会减小。如上图所示，点积的结果是对称的，并且随 $|k|$ 增加而减少（但并不单调）。

    但是在 Transformer 中，由于需要经过映射，即两者间的点积实际是 $\vec{p}_t \cdot W \cdot \vec{p}_{t+k}$，下图展示了经过映射之后的位置向量点积：

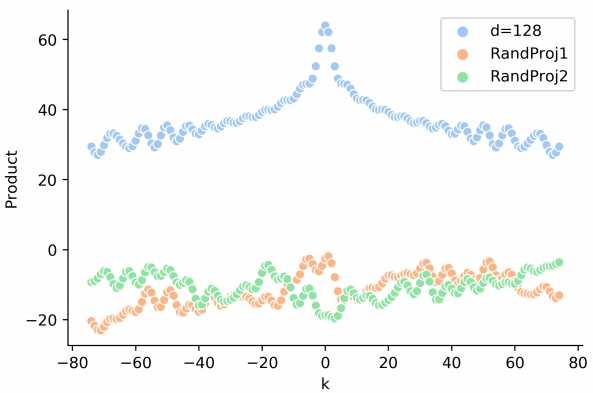
    我们可以看到，此时位置向量的点积并没有展现出明确的趋势。

    ② 对称性

    由此我们发现，$ \vec{p}_t \cdot \vec{p}_{t+k} = \vec{p}_t \cdot \vec{p}_{t-k} $，这说明正弦位置编码无法区分词与词的前后关系。

  • 词向量和位置向量直接相加是否合理？

    Transformer 对模型输入的词向量和位置向量的处理是直接相加，作者并没有给出一个理论解释，为什么要直接相加。但是如果我们读过足够多的的 NLP 论文，我们会发现，对位置向量的处理通常只有两种方法：相加和拼接。这两种处理方式在不同的模型中有不同的表现，但总体上并没有太大的差别。Transformer 之所以使用相加的方式，可能主要是考虑减少模型参数，毕竟自注意力矩阵的参数已经足够多了。

    但是我们仔细考虑一下，无论是直接相加还是拼接，都隐含了一个假设：词向量和位置向量都是独立分布的。这个假设对词向量来说是成立的，因为词向量的 index 与我们使用的字典排序有关，而这个排序是任意的，任意的 index 与 index+k 或者 index-k 都没有任何依赖关系，所以这个假设是成立的。但是对于位置向量却并不满足这一假设，其顺序关系对模型理解文本有着重要的影响。我们称之为位置不敏感问题（position-insensitive problem）。

    为了解决这一问题 Wang 等人提出关于位置的连续函数来表征词在位置上的表示，即：

    其中 $\pmb{g}_j(t) = [g_{j,1}(t), g_{j, 2}(t), …, g_{j, D}(t)]$，$g_{j, d}(t)$ 是一个关于 $t$ 的函数。为了让这个函数更好的表征位置信息，$g_{j, d}(t)$ 必须要满足一下两个性质：

    1. Position-free offset transformation

      存在一个线性函数 $\mathrm{Transform}_k(\cdot)=\mathrm{Transform}(g(t))$ 使得

      也就是说在位置 $t+k$ 上的词 $w_{j,t+k}$ 可以通过位置 $t$ 上的词 $w_{i, t}$ 通过一个只和 $k$ 相关的变换得到，而与具体这个词无关。有点类似正弦位置编码的线性变换，只是这里不仅是位置的变换，还有词的变换。

    2. Boundedness

      这个线性函数必须是有界的。这是一个非常合理的限制，不做过多解释。

    最后，作者提出了 $g(t)$ 的函数形式：

    我们可以看到这是一个复数形式的函数，其中 $r$ 为振幅， $\omega$ 为角频率，$\theta$ 为初相，都是需要学习的参数。

3.2.3 相对位置编码

无论是可学习位置编码还是正弦位置编码都是将位置编码作为额外的信息输入给模型，相对位置编码是将位置信息作为模型本身的属性，使模型不需要额外输入位置编码即可处理序列的位置信息。

这部分因为涉及到的都是模型架构的修改，因此我们会在后续的论文解读中解读相关的论文，这里不做解释。有兴趣的话可以看以下几篇论文（这几篇论文都会在后面详细解读）：

  1. Self-Attention with Relative Position Representations
  2. Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
  3. Gaussian Transformer: A Lightweight Approach for Natural Language Inference

4. Multi-head Attention

4.1 为什么需要 K、Q、V，只用K、Q/K、V/Q、V行不行？

实际上这个问题，我们在 NLP中的注意力机制简介（一） 这篇文章中介绍过了。最初的注意力机制实际上是只用了两个值的，直到 Sukhbaatar et al., 2015 将注意力机制引入到对话系统模型中才出现了 $k, q, v$ 三值的注意力形式。这样的注意力形式有两个好处：

  • 可复用性
  • 灵活性

更详细的内容可以参考上面的博客以及论文，这里不赘述。

4.2 自注意力为什么scaled?

知乎上关于这个问题有很详细的讨论与解释，我就不自由发挥了，照抄过来。原文地址：transformer中的attention为什么scaled?

4.2.1 为什么比较大的输入会使得 softmax 的梯度变得很小？

对于输入向量 $\pmb{x} \in \mathbb{R}^d$，softmax 函数将其映射/归一化到一个 $\pmb{\hat{y}} \in \mathbb{R}^d$。这个过程中，softmax 先用一个自然底数 $e$ 将输入的元素距离先拉大，然后归一化为一个分布。假设某个输入 $\pmb{x}_k$ 表示最大的元素，如果输入的数量级变大（每个元素都很大），那么 $\pmb{x}_k$ 对应的 $\pmb{\hat{y}}_k$ 会非常接近 1。

我们可以用一个小例子来看看。假定输入 $\pmb{x} = [a, a, 2a]^T$，

  • $a = 1$ 时，$\hat{y}_2=0.5761168847658291$；
  • $a=10$ 时，$\hat{y}_2 = 0.999909208284341$；
  • $a = 100$ 时，$\hat{y}_2 \approx 1$ （计算机精度限制）。

我们不妨把不同的 $a$ 对应的 $\hat{y}_2$ 绘制成一条曲线，更能清晰的看出问题。

1
2
3
4
5
6
7
8
from math import exp
from matplotlib import pyplot as plt
import numpy as np 
f = lambda x: exp(x * 2) / (exp(x) + exp(x) + exp(x * 2))
x = np.linspace(0, 100, 100)
y_3 = [f(x_i) for x_i in x]
plt.plot(x, y_3)
plt.show()

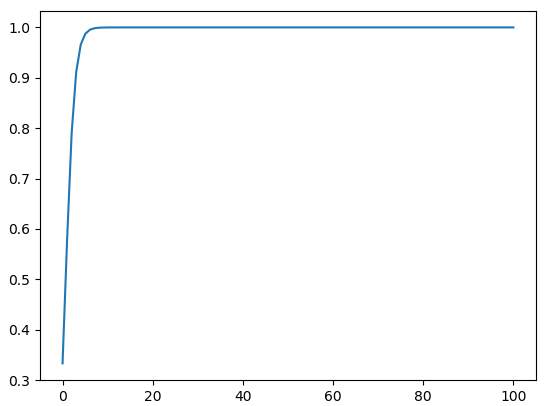
可以看到，数量级对 softmax 得到的分布影响非常大。在数量级较大时，softmax 将几乎全部的概率分布都分配给了最大值对应的标签。这里的数学证明请参考文章：浅谈Softmax函数（见A.补充）。

然后我们来看 softmax 的梯度。不妨简记 softmax 函数为 $g(\cdot)$，$\pmb{\hat{y}} = g(\pmb{x})$ 对 $\pmb{x}$ 的梯度为：

根据前面的讨论，当输入 $ \pmb{x}$ 的元素均较大时，softmax 会把大部分概率分布分配给最大的元素。假设我们的输入数量级很大，最大的元素是 $\pmb{x}_1$，那么就将产生一个接近 one-hot 的向量 $\pmb{\hat{y}} = [1, 0, \cdots, 0]^T$，此时此时上面的矩阵变为如下形式：

也就是说，在输入的数量级很大时，梯度消失为0，造成参数更新困难。

4.2.2 维度与点积大小的关系是怎么样的，为什么使用维度的根号来放缩？

假设向量 $\pmb{q}$ 和 $\pmb{k}$ 的各个分量是相互独立的随机变量，均值是 $0$，方差为 $1$，则点积 $\pmb{q \cdot k}$ 的均值为 $0$，方差为 $d_k$，$d_k$ 表示向量维度。这里给出一点详细的推导：

$\forall i = 1, …, d_k$，$q_i$ 和 $k_i$ 都是随机变量。为方便书写，不妨记 $X = q_i, Y=k_i$。已知：$D(X) = D(Y) = 1$ ， $E(X)=E(Y)=0$。

则有：

  1. $E(XY)=E(X)E(Y) = 0 \times 0 = 0$

由期望和方差的性质， 对相互独立的分量 $Z_i$ 有：

所以 $\pmb{q} \cdot \pmb{k}$ 的均值 $E(\pmb{q \cdot k}) = 0$，方差 $D(\pmb{q \cdot k}) = d_k$。方差越大也就说明，点积的数量级越大（以越大的概率取大值）。那么一个自然的做法就是把方差稳定到 1，做法是将点积除以 $\sqrt{d_k}$：

将方差控制为 1，也就有效地控制了前面提到的梯度消失的问题。

4.2.3 为什么在其他 softmax 的应用场景，不需要做 scaled?

参考：Massive Exploration of Neural Machine Translation Architectures

具体来说，分为以下两个层面：

  • 为什么在普通形式的 attention 中，使用非 scaled 的 softmax？

    最基础的注意力机制有两种形式， 一种是加性的，另一种是乘性的。数学描述为：

    在计算自注意力的时候之所以用乘性注意力机制，主要是为了计算更快。因为虽然矩阵加法的计算更简单，但是加性注意力包含 $\tanh$ ，相当于是一个完整的神经网络层。在整体计算复杂度上两者接近，但是矩阵乘法已经有了非常成熟的加速实现。在 $d_k$ 较小的时候两者效果接近，但随着 $d_k$ 增大，加性效果开始明显超越乘性注意力。

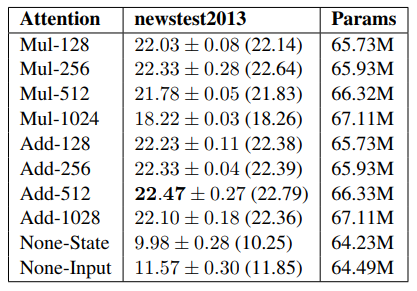
    作者分析乘性注意力效果不佳的原因，认为是极大的点积值将整个 softmax 推向梯度平缓区，使得收敛困难。也就是上面讨论的梯度消失。这才有了 scaled。所以加性注意力机制天然不需要 scaled，在乘性注意力中，$d_k$ 较大的时候必须要做 scaled。

    那么，极大的点积值是从哪里来的呢？

    乘性注意力的极大点积值的来源上面讨论过，是由于两向量点积方差会从 $[0, 1]$ 范围扩散到 $[0, d_k]$ 范围。而加性的注意力，由于存在 $\tanh$ 将值限制在 $[-1, 1]$ 范围内，整体的方差和 $d_k$ 没有关系。

  • 为什么在分类层（最后一层），使用非 scaled 的 softmax？

    同上面部分，分类层的 softmax 也没有两个随机变量相乘的情况。此外，这一层的 softmax 通常和交叉熵联合求导，在某个目标类别 $i$ 上的整体梯度会变成 $\pmb{y}’_i-\pmb{y}_i$，即预测值与真值的差。当出现某个极大值时，softmax 的输出概率会集中在该类别上。如果预测正确，整体梯度接近于 0，如果类别错误，整体梯度会接近于 1，给出最大程度的负反馈。

    也就是说，这个时候的梯度形式改变，不会出现极大值导致梯度消失的情况。

4.3 Transformer 为什么要用 Multi-head？

Multi-head 应该是借鉴的 Multi-dimension attention 的思想。最早由 Wang et al., 2017 提出 2D-attention，希望模型能在不同的语境下，关注句子中不同的点。后来由 Lin et al. 2017 将 2D-attention 扩展到 Multi-dimension attention 。多维注意力的初衷是使注意力形成多个子空间，可以让模型去关注不同方面的信息，多头注意力也继承了这一想法。但是在实际的训练中，模型真的如我们的预期那样，去学习了不同方面的特征吗？

现在的研究表明，Transformer 的底层更偏向于关注语法，顶层更偏向于关注语义。虽然在同一层中多数头的关注模式是一样的，但是总有那么一两个头与众不同。这种模式是很普遍的，为什么会出现这种情况？目前还不清楚。

针对不同的头，我们思考以下几个问题：

  • 同一层中，不同头之间的差距有多少？（用 $h_i$ 度量）
  • 同一层中，不同头的数量是否对 $h_i $ 有影响？
  • $h_i$ 是否随层数的变化而变化？
  • 我们能否使用 single-head 达到 multi-head 的效果？

另外，初始化对 $h_i$ 的影响也是一个值得探究的问题，这个我们专门开一篇文章讲解，这里略过。

论文 What Does BERT Look At? An Analysis of BERT’s Attention 研究指出，头之间的差距随着所在层数变大而减少。换句话说，头之间的方差随着所在层数的增大而减小。

而在论文 Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned 中，作者研究了翻译的质量在何种程度上依赖单个头以及能否去掉一些头而不失效果等问题。研究结果表明，只有一小部分头对翻译而言是重要的，其他的头都是次要的（可以丢掉）。 这说明注意力头并非越多越好，但要足够多，single-head attention 目前来看还是无法取代 multi-head attention。

另外，其实还有一个有意思的问题是，不同头之间的差距有什么作用？在 Lin et al. 2017 的这篇文章中，通过引入一个正则化项，将不同头之间的注意力差距变大。他给出的解释是，是模型尽可能多的关注到不同的点上。那么拉大注意力头之间的差距在 Transformer 中有什么效果，目前还没有相关的实验。

更多关于 Multi-head attention 的探讨可以参考：

5. Add & Norm

还记得我们在介绍 Transformer 的时候，模型训练的初期我们使用了 warm-up 的小技巧。那么问题就来了，warm-up 为什么有效？

On Layer Normalization in the Transformer Architecture 就试图从 LayerNorm 的角度去解释。

首先我们先思考：为什么 warm-up 是必须的？能不能把它去掉？本文的出发点是：既然 warm-up 是训练的初始阶段使用的，那肯定是训练的初始阶段优化有问题，包括模型的初始化。顺着这个思路，作者发现在训练的初始阶段，输出层附近的期望梯度非常大，如果没有 warm-up，模型优化过程就会炸裂，非常不稳定。使用 warm-up 既可以保持分布的平稳，也可以保持深层的稳定。

作者发现这一现象与 LayerNorm 的位置有关。在原始的 Transformer 中，LayerNorm 在跟在 Add 之后的（也就是跟在残差之后），我们把这个称为 Post-LN Transformer。那我们很自然的想到，如果我们把 LayerNorm 换个位置，比如放到残差计算过程中（称为Pre-LN Transformer）会怎么样呢？

下图是两种结构的示意图：

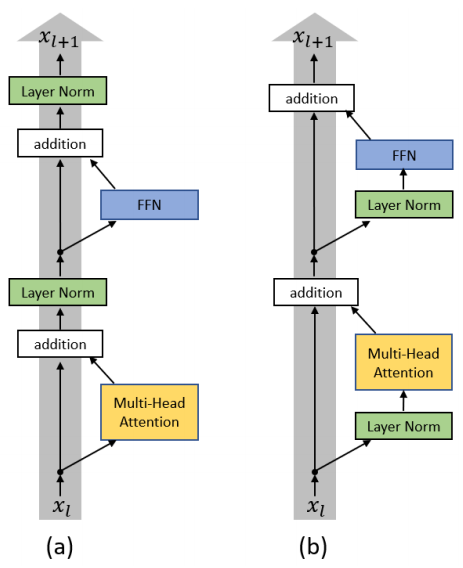
作者通过理论证明了：

  • Post-LN Transformer的梯度范数在输出层附近很大，因此很可能随着后向传播的进行梯度越来越小；
  • Pre-LN Transformer在每层的梯度范数都近似不变。

因此， warm-up 对 Post-LN Transformer 来说是必不可少的，实验结果也证实了这一点。而对于 Pre-LN Transformer 来说，理论上 warm-up 是可有可无的。然后作者通过实验证明 Pre-LN Transformer 似乎的确不再需要 warm-up 了。

6. Masked Multi-head Attention

Mask 在 NLP 中是一个很常规的操作，也有多种应用的场景和形式。那么 Mask 到底有什么用呢？先上结论：

  • 处理非定长序列
  • 防止标签泄露

总的来说 Mask 无非就是这两种用途，下面我们详细解释一下。

6.1 处理非定长序列

在 NLP 中，文本一般是不定长的，所以在进行训练之前，要先进行长度的统一，过长的句子可以通过截断到固定的长度，过短的句子可以通过 padding 增加到固定的长度，但是 padding 对应的字符只是为了统一长度，并没有实际的价值，因此希望在之后的计算中屏蔽它们，这时候就需要 Mask。

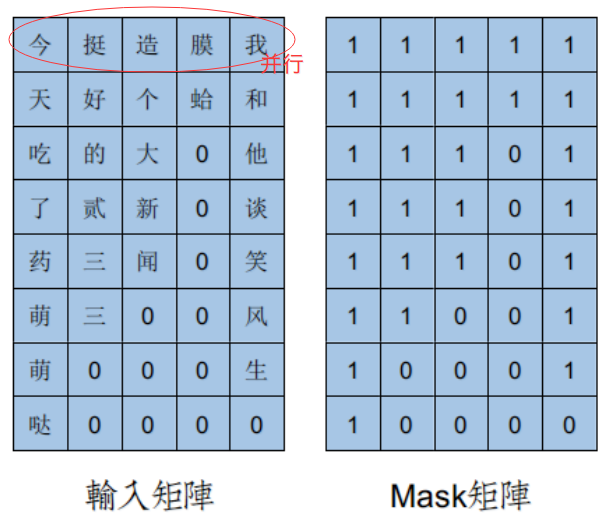
上图中的 1 表示有效字，0 代表无效字。

  • RNN 中的 Mask

    对于 RNN 等模型，本身是可以直接处理不定长数据的，因此它不需要提前告知序列长度。但是在实践中，为了 批量训练，一般会把不定长的序列 padding 到相同长度，再用 mask 去区分非 padding 部分和 padding 部分。做这样区分的目的是使得 RNN 只作用到它实际长度的句子，而不会处理无用的 padding 部分，这样 RNN 的输出和隐状态都会是对应句子实际的最后一位。另外，对于 token 级别的任务，也可以通过 mask 去忽略 padding 部分对应的 loss。

  • Attention 中的 Mask

    在 Transformer 中，有两种不同的 Mask。其中作用在序列上的 Mask 同样是为了忽略 padding 部分的影响。

6.2 防止标签泄露

在一些任务中，模型输入的序列中可能包含需要预测的一些信息，为了防止模型“提前看答案”，我们需要将输入序列中的一些信息 mask 掉。

  • Transformer 中的 mask

    Transformer 中 masked multi-head attention 中的 mask 目的就是掩盖输入序列中的一些信息。在进行机器翻译的时候，模型 decoder 的输入是目标序列（已经预测的部分），比如 $t$ 时刻，模型是不可能知道 $t+1$ 时刻的输入的，因此，在训练的时候我们要模拟这一过程。至于怎么样进行 mask 这个在 Transformer 的介绍中已经详细介绍过了，不再赘述。

  • BERT 中的 Mask

    BERT 实际上是 Transformer 的 Encoder，为了在语言模型的训练中，使用上下文信息又不泄露标签信息，采用了 Masked LM，简单来说就是随机的选择序列的部分 token 用 [Mask] 标记代替。至于这么做为什么有效，实际上 Data Noising as Smoothing in Neural Network Language Models 就首次提出了此方法，而且给出了理论解释。这种替换其实本质上属于语言建模里面基于 interpolation 的平滑方式。

  • XLNet 中的 Mask

    XLNet 通过 Permutation Language Modeling 实现了不在输入中加 [Mask]，同样可以利用上下文信息。

    为了更直观的解释，我们举个例子：

    假设输入的序列是[1,2,3,4], 排列共有 4x3x2=24 种。

    选其中的四种分别为[3,2,4,1],[2,4,3,1],[1,4,2,3],[4,3,1,2]。

    在预测位置3的单词时，

    第一种排列看不到任何单词，第二种排列能看到[2,4]

    第三种排列能看到[1,2,4],第四种排列能看到[4],

    所以预测位置 3 的单词时，不仅能看到上文[1,2],也能看到下文的[4]。

关于 Mask 的讨论也就到此为止了。

同时关于 Transformer 中的一些细节，以及引申出来的一些讨论，我们也就介绍到这。

7. Appendix

Appendix A： BPE 初始版本

假设有一段序列 $aaabdaaabac$，我们想对其进行编码。通过观察我们会发现 $aa$ 的出现概率最高（只考虑字符对），那么我们用一个序列中没有出现过的字符 $Z$ 来代替 $aa$ ：

得到新序列之后我们会发现 $ab$ 字符对出现的概率最高，同样的我们使用一个新序列中没有出现过的字符 $Y$ 来代替 $ab$ ：

继续重复上面的步骤，我们得到：

最后，序列中的所有字符对出现的频率都是 1，BPE 编码结束。解码的时候按照相反的顺序更新替换即可。

Reference

  1. Neural machine translation of rare words with subword units. Rico Sennrich, Barry Haddow, Alexandra Birch. 2015. arXiv: 1508.07909
  2. Japanese and Korean Voice Search. Schuster, Mike, and Kaisuke Nakajima. 2012. IEEE
  3. BPE-Dropout: Simple and Effective Subword Regularization. Ivan Provilkov, Dmitrii Emelianenko, Elena Voita. 2019. arXiv:1910.13267
  4. Subword regularization: Improving neural network translation models with multiple subword candidates. Taku Kudo. 2018. arXiv: 1804.10959
  5. 深入理解NLP Subword算法：BPE、WordPiece、ULM Luke. 知乎
  6. 子词技巧：The Tricks of Subword Andy Yang. 知乎
  7. 一分钟搞懂的算法之BPE算法
  8. Transformer Architecture: The Positional Encoding
  9. Linear Relationships in the Transformer’s Positional Encoding Timo Denk’s Blog
  10. Encoding Word Oder In Complex Embeddings Benyou Wang, Donghao Zhao, Christina Lioma, Qiuchi Li, Peng Zhang, Jakob Grue Simonsen. 2020. ICLR
  11. 如何优雅地编码文本中的位置信息？三种positioanl encoding方法简述 小鹿鹿 lulu, 微信公众号
  12. How Much Attention Do You Need? A Granular Analysis of Neural Machine Translation Architectures Tobias Domhan. 2018. ACL
  13. Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned Elena Voita, David Talbot, Fedor Moiseev, Rico Sennrich, Ivan Titov. 2019. arXiv: 1905.09418
  14. Are Sixteen Heads Really Better than One? Paul Michel, Omer Levy, Graham Neubig. 2019. arXiv: 1905.10650
  15. On Layer Normalization in the Transformer Architecture Ruibin Xiong, Yunchang Yang, Di He, Kai Zheng, Shuxin Zheng, Huishuai Zhang, Yanyan Lan, Liwei Wang, Tie-Yan Liu. 2020. ICLR (rejected)
  16. NLP中的Mask全解，海晨威 PaperWeekly
  17. 关于Transformer的若干问题整理记录 Adherer 知乎
  18. 香侬读 | Transformer中warm-up和LayerNorm的重要性探究 香侬科技， 知乎
  19. transformer中的attention为什么scaled?
  20. Massive Exploration of Neural Machine Translation Architectures, Denny Britz, Anna Goldie, Minh-Thang Luong, Quoc Le. 2017. arXiv: 1703.03906
  21. TENER: Adapting Transformer Encoder for Named Entity Recognition Hang Yan, Bocao Deng, Xiaonan Li, Xipeng Qiu. 2019. arXiv:1911.04474
 上一页

Transformer pytorch

 评论