NLP中的注意力机制简介（二）

Rogerspy

2019-08-27

NLP

字数统计: 5.6k字 | 阅读时长≈ 23分

——Transformer专题篇

1. 前言

之前我们介绍了各种各样的注意力机制，如果仔细回想一下就可以发现无论是哪种注意力机制都不是单独出现的，都是伴随着RNN或者其他RNN的变种。这种基于RNN的注意力机制会面临一个问题就是，难以处理长序列的句子，因为无法实现并行计算，所以非常消耗计算资源。

CNN虽然可以实现并行计算，但是它无法获得序列的位置信息，这样它也就难以获得远距离信息上的依赖关系。后来虽然有人提出了完全基于CNN的seq2seq模型，但是却非常消耗内存。

由于基于RNN的注意力机制遇到了计算资源上的瓶颈，Vaswani et al., 2017提出了一个新的模型——Transformer！从目前的发展来看，这个模型对得起这个名字，因为它真的很能打，自从2018年基于Transformer的BERT预训练语言模型的横空出世到今天，几乎每一次NLP的重大进展都与它息息相关。因此，我们专门开一个专题篇来详细介绍一下这个模型。

Transformer的创新点在于抛弃了之前传统的基于CNN或者RNN的encoder-decoder模型的固有模式，只用Attention实现encoder-decoder。Transformer的主要目的在于减少计算量和提高并行效率的同时不损害最终的实验结果。

2. 模型结构

2.1 模型结构总览

在初始的论文中Transformer仍然是被用于机器翻译任务上：

下面我们来打开擎天柱，看下它到底是怎么构成的？

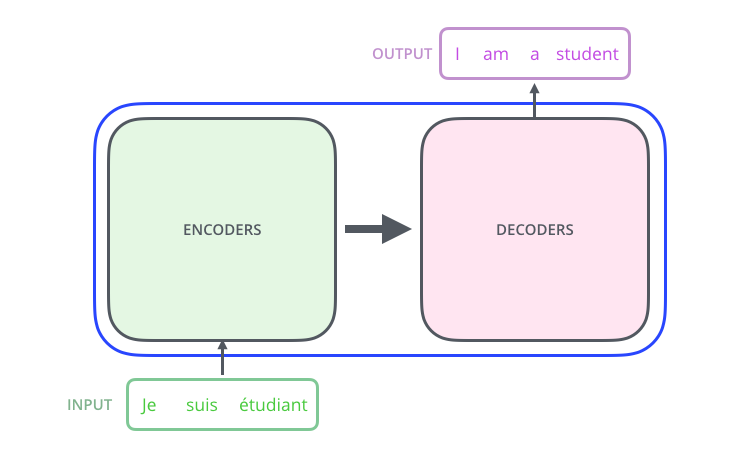
可以看到Transformer仍然采用了encoder-decoder结构，原始论文中encoder是由6个相同的编码模块堆叠而成（这里的相同指的是结构相同，但是其中的权重却是不共享的，下面的解码器与之相同），而decoder同样也是用6个解码器堆叠而成的。6这个数字并没有什么特殊之处，只是原始论文使用的层数，我们可以在实验过程中任意设置层数。如下图所示：

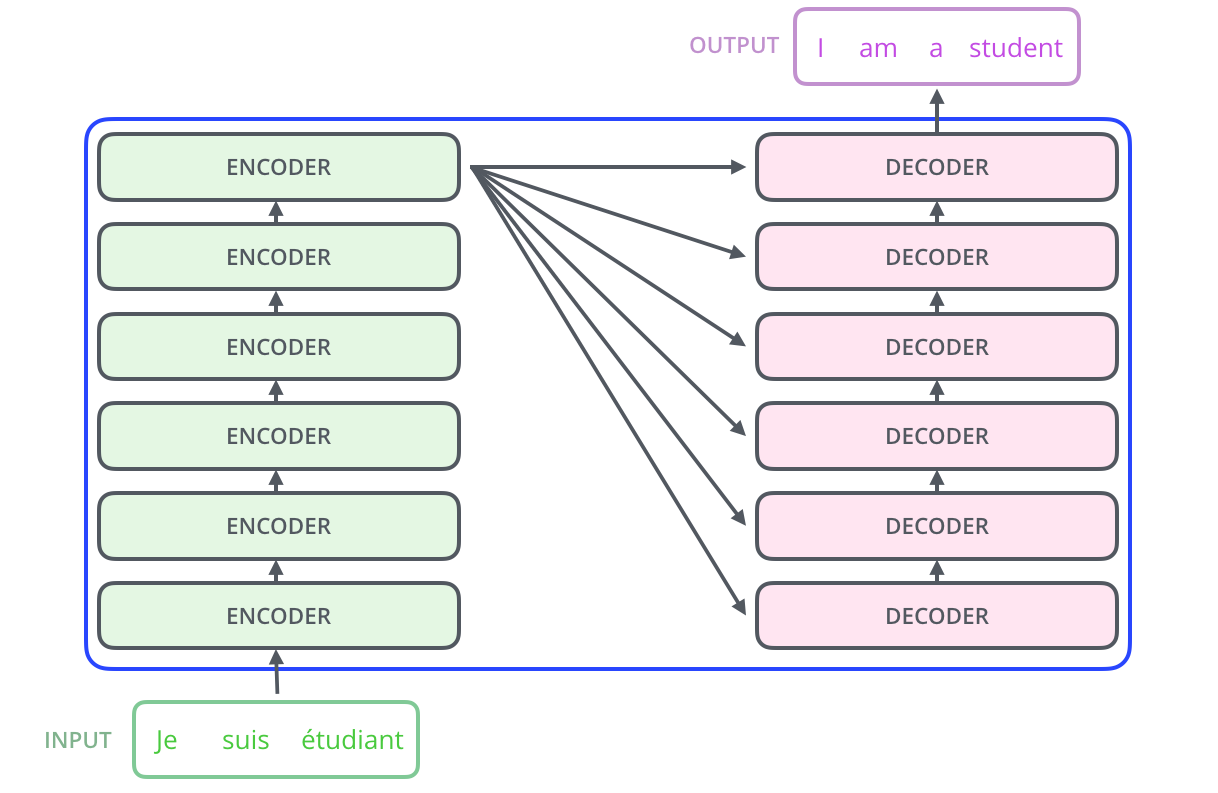
注意一个细节，encoder和decoder的链接方式是encoder的最后一层输出与decoder的每一层相连。下面我们打开其中一个编码器和解码器看下里面是什么结构：

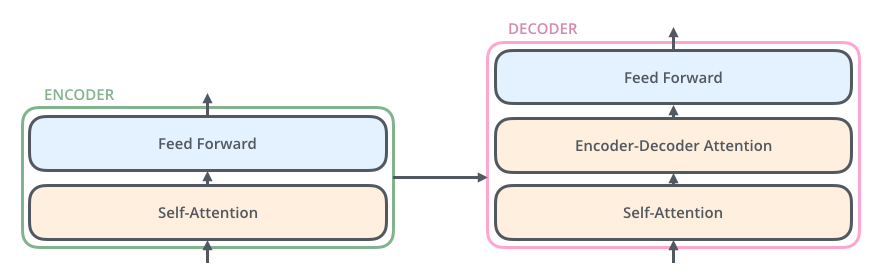
encoder的输入先经过一个自注意力层对句子进行编码获取词的注意力权重，然后将自注意力输入给一个全连接层。

对于decoder中自注意力层和全连接层和encoder相同，但是在自注意力输出后要经过一个注意力编码层与encoder进行联合编码，然后再传入给全连接层。这个联合编码其实就类似于在seq2seq模型中解码过程中，decoder隐状态和注意力联合编码然后再输出的过程是类似的。

下面我们继续拆解擎天柱的零件，看看这个自注意力和全连接层下面埋藏着什么秘密。

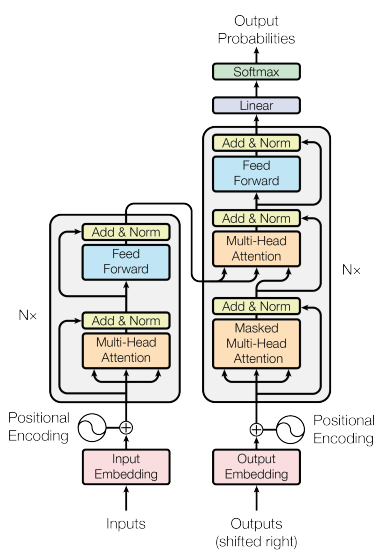
原来所谓的Self-attention是一个叫做Multi-Head Attention的东西，这个就是擎天柱的核心部件了。其他的小零件比如Add, Norm, Linear, softmax, Feed Forward等等都是在五金店都能买到的小玩意儿。下面我们就详细看下这个能量块到底隐藏着什么秘密吧。

2.2 Multi-Head Attention

从字面上就可以看出所谓Multi-Head Attention是由两部分组成——Multi-Head和Attention，而实际情况也是如此。其实严格来讲这是一个一般化的名称，如果具体到论文使用的自注意力机制的话，应该叫做Self-Multi-Head Attention。应该有三部分组成，除了上面提到的两个，还应该加上一个自注意力。

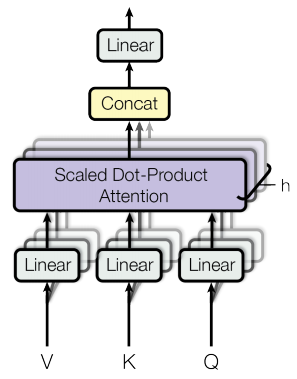
还记得我们上一篇介绍注意力机制的文章中提到一种使用$\mathbf{k}, \mathbf{q}, \mathbf{v}$计算注意力的注意力机制。而Scaled Dot-Product也是我们之前提到的一种计算Alignment score function的方法。也就是说，图中下半部分是在计算Scaled-Dot Product Attention，而图中上半部分的Concat操作就是拼接操作，拼接什么？仔细看下半部分计算注意力的时候，不是只计算一个Scaled-Dot Product Attention，而是在同时计算h个Scaled-Dot Product Attention。而Concat拼接的的就是这h个Scaled-Dot Product Attention。这就是所谓的Multi-Head Attention，每一个Head就是一个Scaled-Dot Product Attention。

形式化描述如下：

$MultiHead(Q, K, V) = Concat(head_1, head_2, ..., head_h)W^O$ $head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)$

其中$W_i^Q \in \mathbb{R}^{d_{model}\times d_q}$，$W_i^K \in \mathbb{R}^{d_{model}\times d_k}$，$W_i^V \in \mathbb{R}^{d_{model}\times d_v}$，$W_i^O \in \mathbb{R}^{d_{model}\times d_o}$。在原始论文中$h=8$，$d_k=d_v=d_{model}/h=64$。由于对每一个Head进行了降维，所以总的计算量和使用一个单独的不降维的Head是一样的。本文涉及到的公式所用标记都与原论文保持一致，避免混淆。

我们仔细思考一下这个Multi-Head Attention，和我们提到的Multi-dimensional Attention有异曲同工之妙。论文里提到，相对于使用单个注意力而言，使用Multi-Head能获得更好的效果。但是论文并没有解释为什么。我们这里结合Multi-dimensional Attention做一个大胆的猜想：Transformer的强大之处正是由于这个Multi-Head！因为多维注意力机制能够获得一句话中在不同语境下的不同理解。而在语言模型中，词语和句子的歧义性一直是自然语言处理的难点，而Transformer在多维注意力机制的作用下能够很好的获取句子的多重含义，并且能根据上下文信息自动获取正确的语义，因此Transformer能够在预训练语言模型中大放异彩。

下面我们就应该看一下这个核心中的核心——Scaled-Dot Product Attention了。

2.3 Scaled-Dot Product Attention

Scaled-Dot Product Attention结构如图所示：

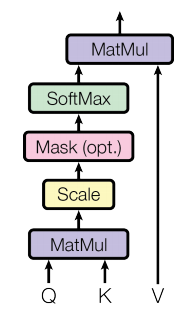
首先我们先给出其形式化定义：

$Attention(K, Q, V) = softmax(\frac{QK^T}{\sqrt {d_k}})V$

我们把图中结构分解开来，一步一步解释清楚：

第一步MatMul：计算Alignment score function

$MatMul(Q, K_i) = QK_i^T$

第二步Scale：调节Alignment score function分数

$Scale(Q, K_i) = \frac{Q,K_i^T}{\sqrt{d_k}}$

第三步Mask（可选）：encoder不需要这一步，decoder需要这一步。

这里的masked就是要在训练语言模型的时候，不给模型看到未来的信息，让模型自己预测下一个词。

第四步Softmax：相似度归一化

$\alpha_i = Softmax(Q, K_i) =softmax(\frac{QK_i^T}{\sqrt {d_k}})$

第五步MatMul：通过计算出来的权重与$V$加权求和得到最终的Attention向量

$Attention(K_i, Q, V_i) = \sum_i \alpha_i V_i$

下面我们从序列输入开始详细解释一下每一步到底是在做什么。

第一步：计算K, Q, V

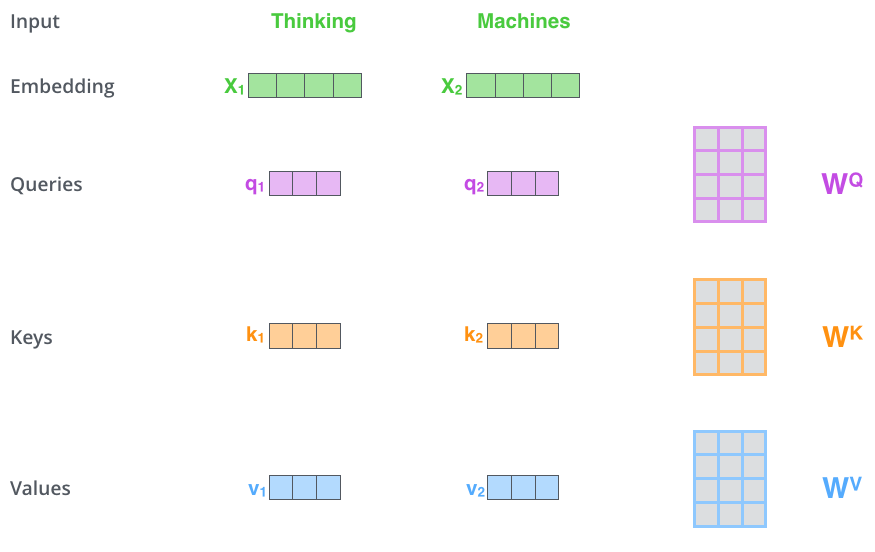
将输入的每一个词转化成词向量，词向量可以是预训练好的（比如用word2vec）词向量，在网络训练过程中固定词向量矩阵不参与训练，也可以是随时初始化，然后随着网络的训练不断更新词向量矩阵。

将序列中每个元素对应的词向量分别与$W^Q, W^K, W^V$相乘计算得到queries, keys, values。计算得到的queries, keys, values的维度为64，当然维度缩减并非必须。

第二步：计算自注意力的alignment score function

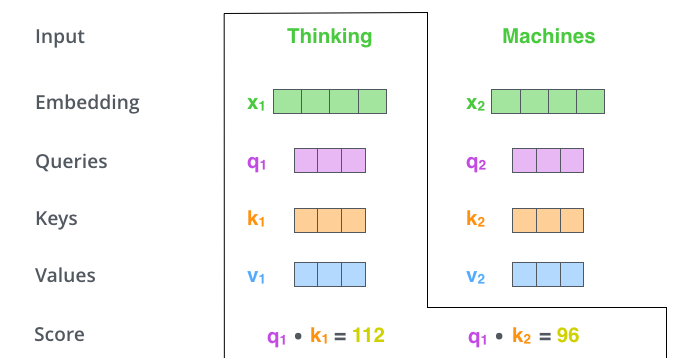
所谓自注意力就是计算序列中两两元素之前的依赖关系，这个分数表示当前这个词需要把多少注意力放在句子中的其他部分上。

以上图举例，Thinking的得分是$\mathbf{q}_1\cdot \mathbf{k}_1=112$，Machines的得分是$\mathbf{q}_1\cdot \mathbf{k}_2=96$，后面的以此类推。

第三步和第四步：对上一步的得分进行缩放，然后计算softmax

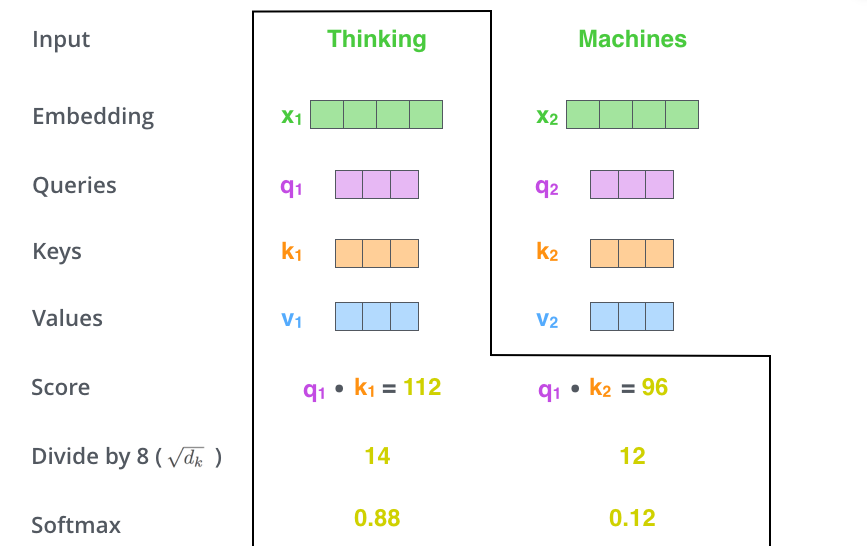
上一步的得分除以8（因为前面我们提到queries, keys, values的维度为64，开方之后就是8）。之所以要做这个缩放论文给出的解释是防止这个得分过大或者过小，在做softmax的时候不是0就是1，这样的话就不够soft了。

得到放缩后的得分之后就是计算softmax了。

第五步：在decoder中对句子进行Mask。比如输入是一句话 “i have a dream” 总共4个单词，这里就会形成一张4x4的注意力机制的图：

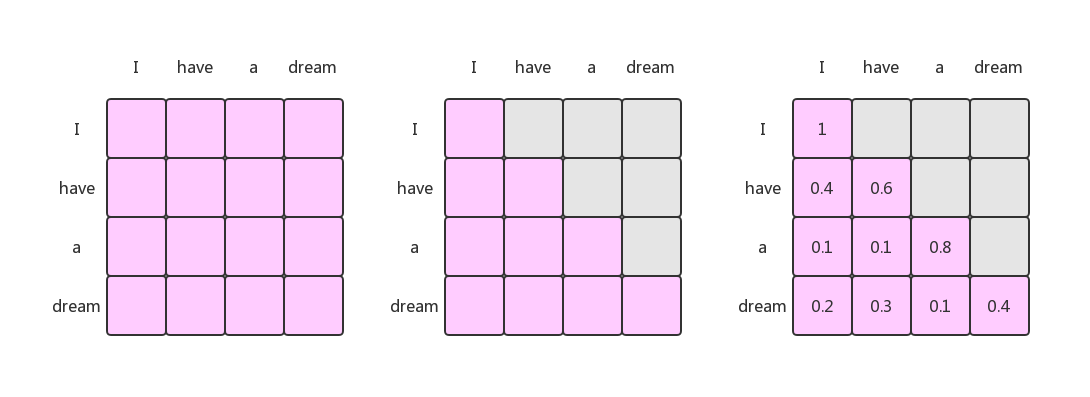
这里的mask就是要在做语言建模的时候，不给模型看到未来的信息，让模型自己预测后面的信息。比如上图中，“I”作为第一个词，只能和自己进行Attention；“have”作为第二个词，可以和“I”和“have”本身进行Attention；“a”作为第三个单词，可以和“I”，“have”，“a” 三个单词进行Attention；到了最后一个单词“dream”的时候，才有对整个句子4个单词的attention。

第六步：用上面计算出来的softmax与values进行加权求和

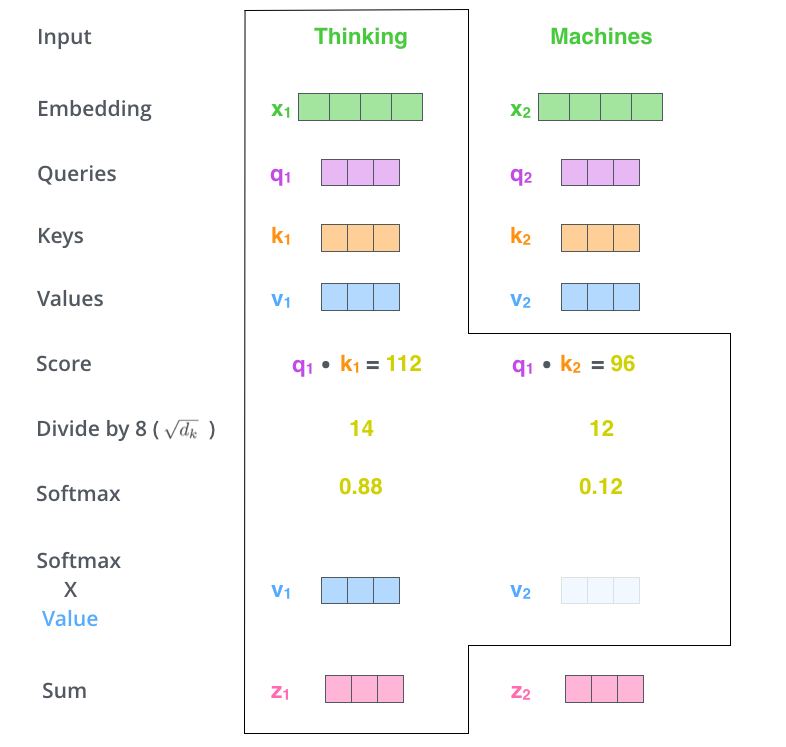
至此Scaled-Dot Product Attention就计算完了。

2.4 矩阵计算 Scaled-Dot Product Attention

前面我们说过，Transformer的初衷就是并行计算，所谓并行计算就是矩阵计算，上面的例子是通过一个一个向量进行计算的，如果我们把向量堆叠成矩阵，就可以实现并行运算了：

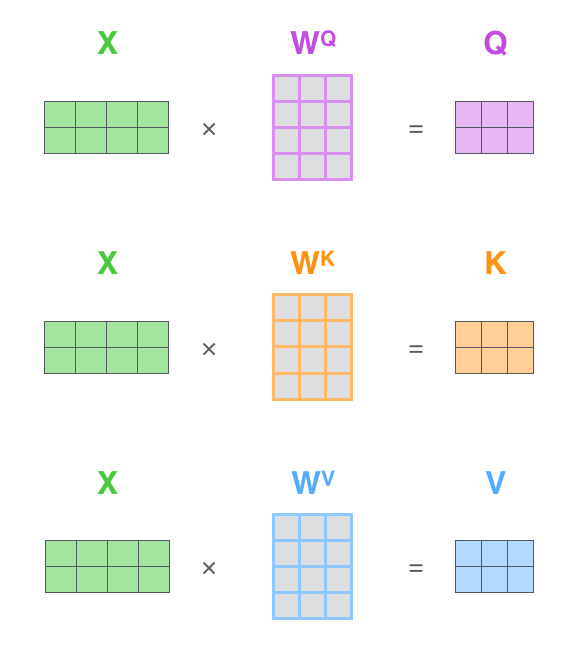
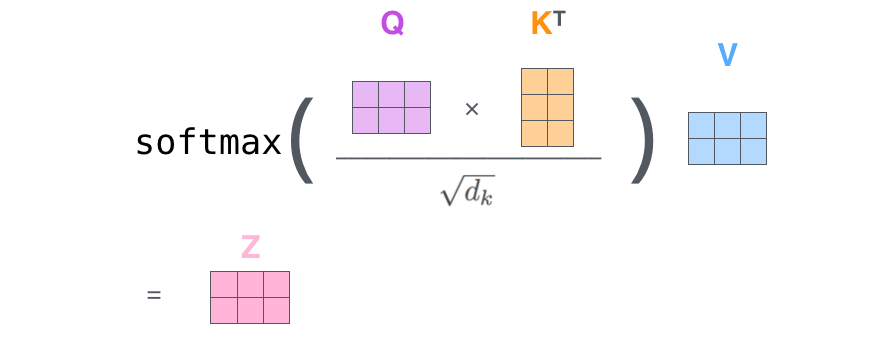
2.5 矩阵计算 Multi-Head

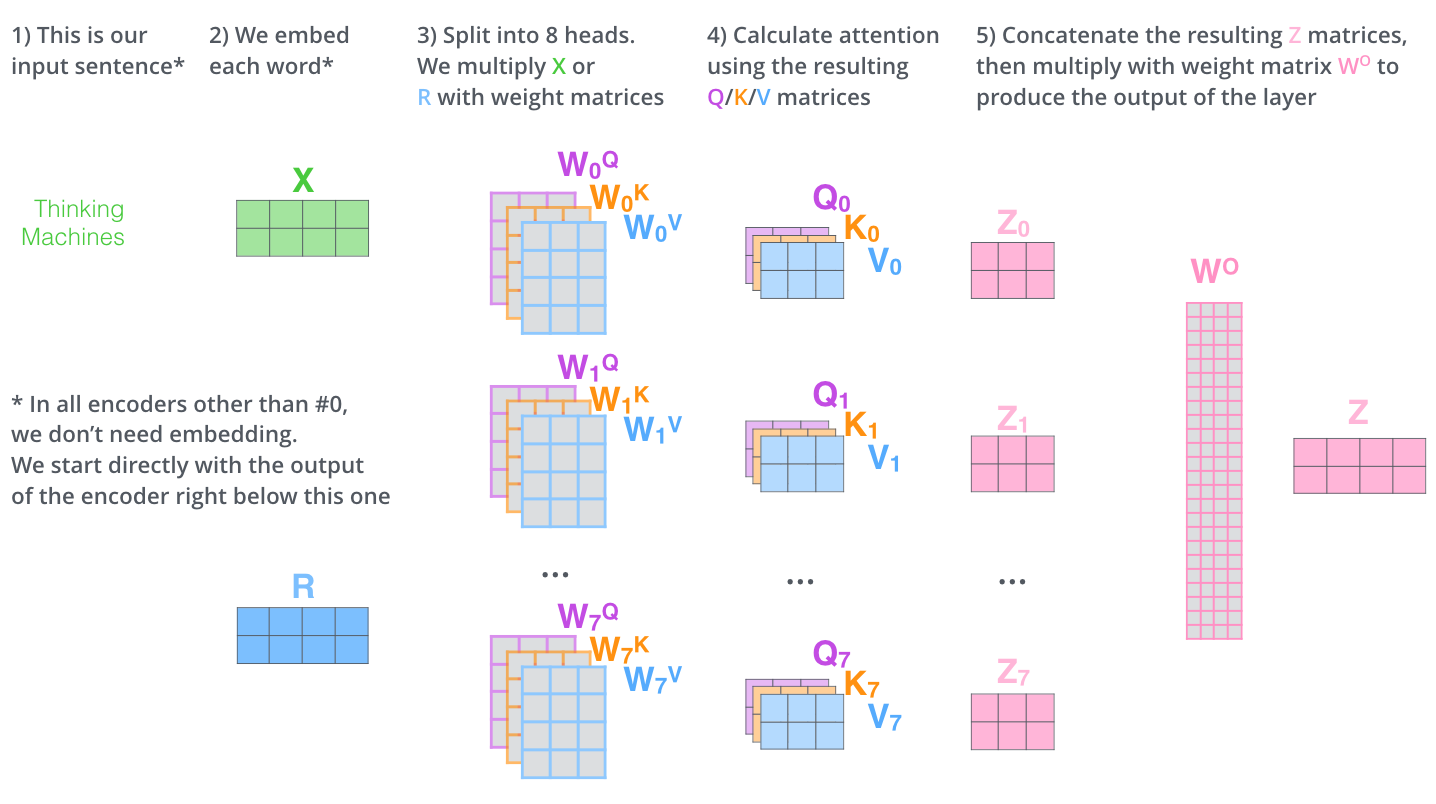
2.6 Position Encoding

到目前为止，擎天柱的能量核心结构我们介绍完了，但是我们还忽略了一个问题：句子是一个有序的序列，句子中两个词的位置互换的话，这个句子的意思完全不同了，因此在处理自然语言的时候词与词的绝对位置或者相对位置也是一个非常重要的信息。

为了解决位置信息的问题，Transformer在每一个输入向量中增加了一个位置向量，这个位置向量的维度为$d_{model}$，这样输入向量和位置向量就可以直接相加了。

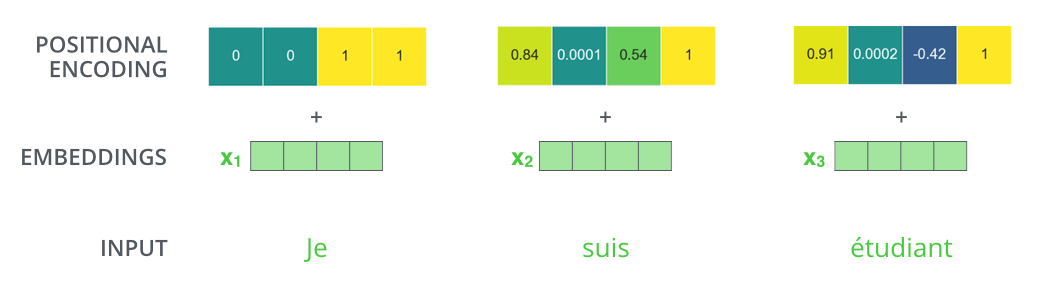
在NLP的很多模型中都有位置向量的使用，比如前面我们提到基于CNN的seq2seq模型（Gehring et al., 2017）。但是通常其他模型中的位置向量都是通过学习得来的，本文采用的是直接通过函数构造出来的：

$\left\{ \begin{aligned} PE_{(pos, 2i)} & = \sin(pos/10000^{2i/d_{model}}) \\\\ PE_{(pos, 2i+1)} & = \cos(pos/10000^{2i/d_{model}}) \end{aligned} \right.$

其中$pos$表示位置索引，$i$表示维度索引。也就是说位置向量中的每一维都是一个余弦曲线，波长是一个从$2\pi$到$10000 \cdot 2\pi$的等比数列。之所以选择这个函数，是因为它允许模型能很容易的学习到相对位置信息，因为对于任意固定的偏置$k$，$PE_{pos+k}$能通过一个$PE_{pos} $的线性函数推理得到：

$\begin{aligned} \sin(\alpha+\beta) &= \sin(\alpha) \cos(\beta) + \cos(\alpha)\sin(\beta)\\\\ \cos(\alpha+\beta) &= \cos(\alpha) \cos(\beta) - \sin(\alpha)\sin(\beta) \end{aligned}$

另外，作者也做过实验，使用通过学习得到的位置向量，最后发现两者的效果差别不大。在效果差别不大的情况下使用直接构造的方法能够避免训练过程的权重更新，这样可以加速训练。另外一个很重要的原因就是，选择这个余弦版本的位置向量还可以处理比训练时遇到的更长的序列。

2.6 残差结构

如果我们仔细看模型结构图就会发现，数据的流向并不是从一层单项流向下一层的这种简单的串联结构，而是采用了类似残差网络的残差式连接。

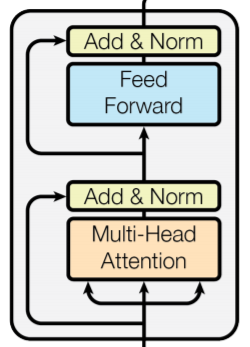
第一步：计算Multi-Head Attention
第二步：原始的输入+Multi-Head Attention
第三步：使用LayerNorm进行正则化
第四步：正则化后的数据经过全连接层，全连接层的激活函数使用ReLU函数。注意这里面的全连接层是每个位置每个位置单独进行计算的，其实更像是卷积核大小为1的卷积层。
第五步：第三步正则化的数据与全连接层后的数据相加
第六步：第五步相加后的数据再次正则化

这就是Transformer的残差网络计算过程。

到目前为止，擎天柱身上的主要零部件我们都已经介绍完了，接下来就该把这些零部件再组装回去了。

3. 模型组装

3.1 Encoder

Encoder包含6个相同的层

每一层包含2个sub-layer：Multi-Head Attention和全连接层。
每个sub-layer都要正则化
sub-layer内部通过残差结构连接
每一层的输出维度为$d_{model}=512$

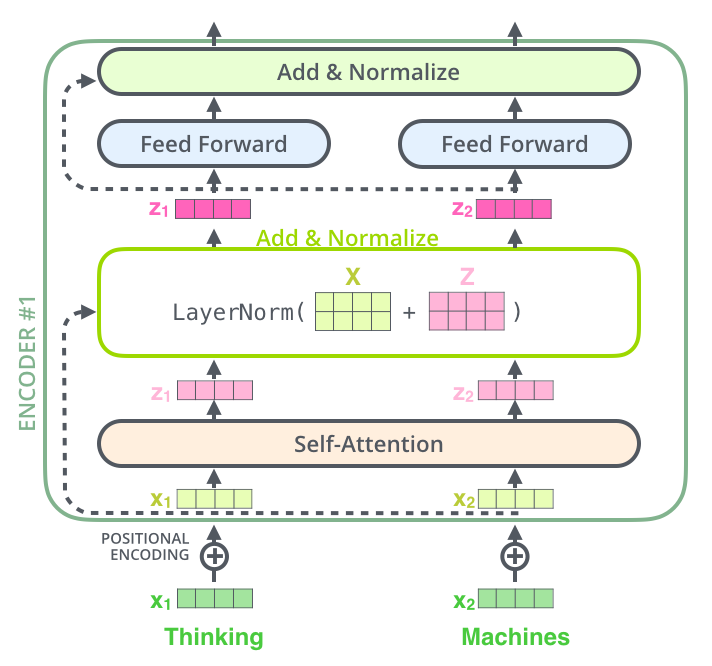
3.2 Decoder

Decoder也是6层

每层包含3个sub-layer：Multi-Head Attention，Encoder-Decoder Attention和全连接层
其中Encoder-Decoder Attention的结构和其他的注意力相同，但是不同的是这一层的$K, V$都是来源于Encoder，而$Q$来源于上一层注意力产生的。
Decoder中的Multi-Head Attention层需要进行修改，因为只能获取到当前时刻之前的输入，因此只对时刻 t 之前的时刻输入进行Attention计算，这也称为Mask操作

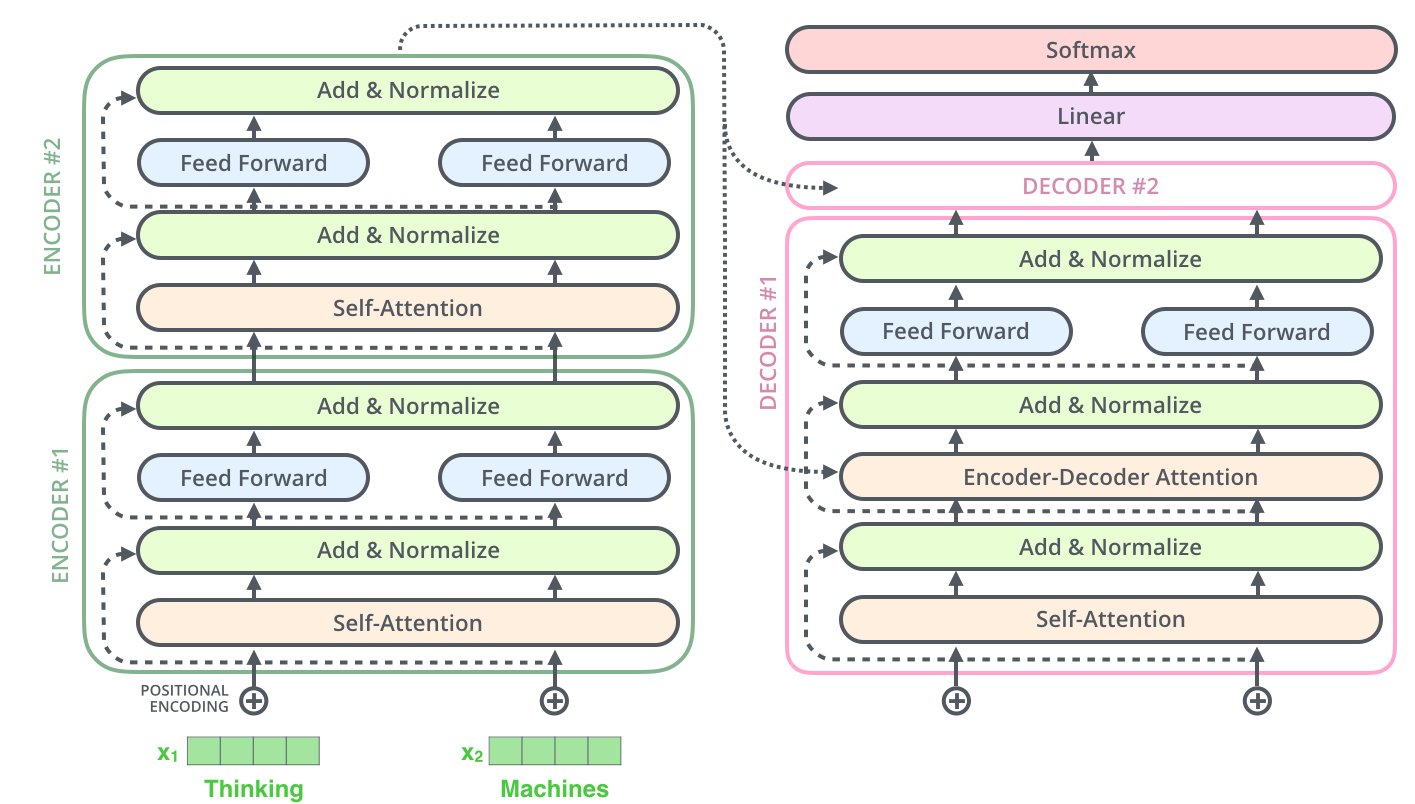
3.3 最后的Linear层和Softmax层

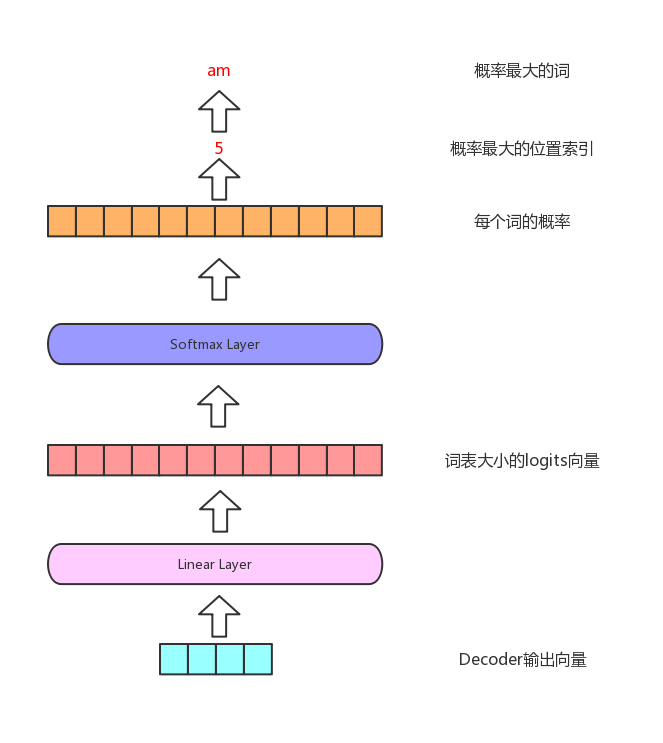
Decoder输出一个向量，我们怎么把这个向量转化成单词呢？这就是最后的Linear和Softmax层做的事情。

线性变换层是一个简单的全连接层，将Decoder输出的向量转化成一个logits vector。假设模型的词表中有10000个词，这个logits vector的维度就是10000，每一维对应词表中的一个词的得分。

然后softmax将这些得分进行归一化，将得分变成每个词的概率，然后选出概率最大的那个位置对应到词就是最后的输出了。

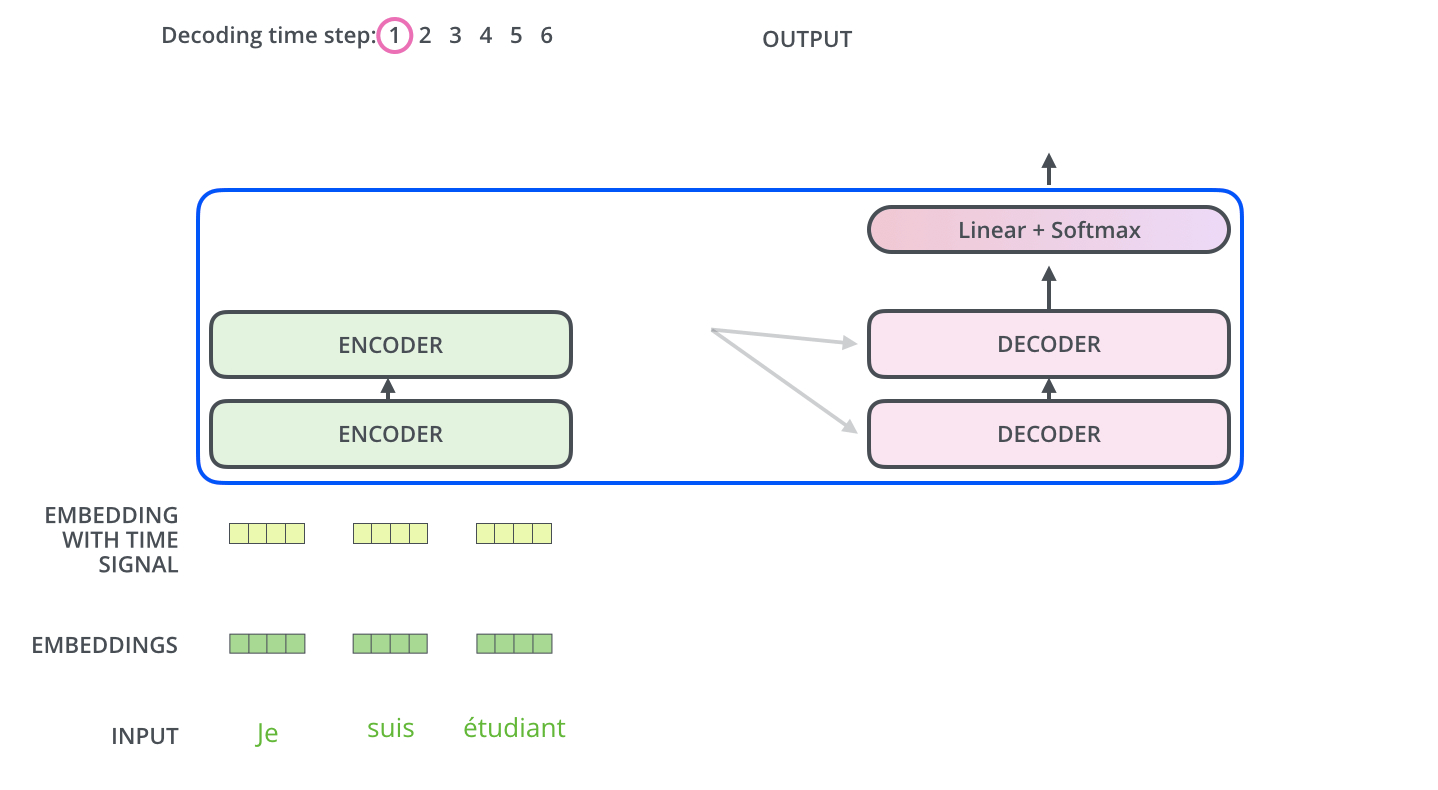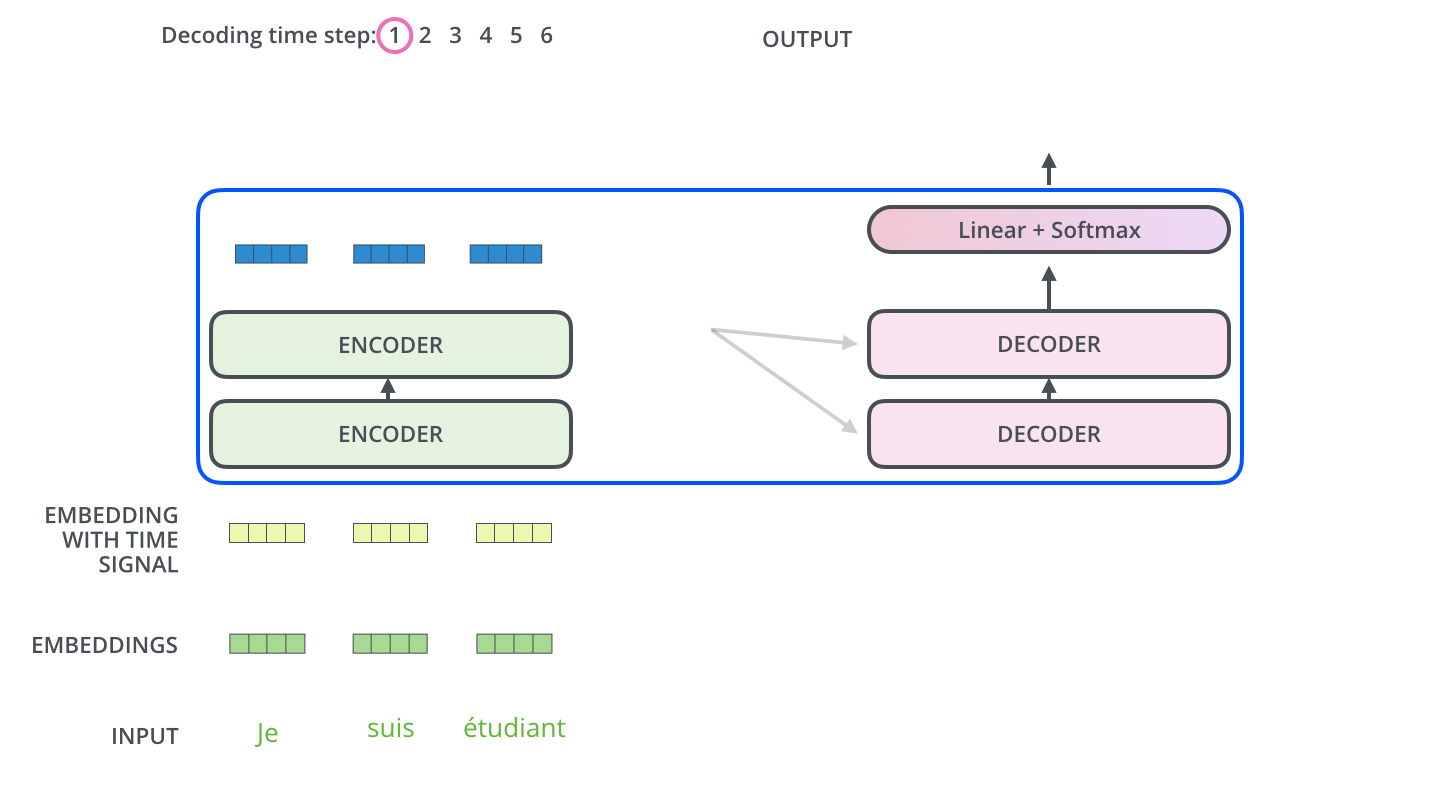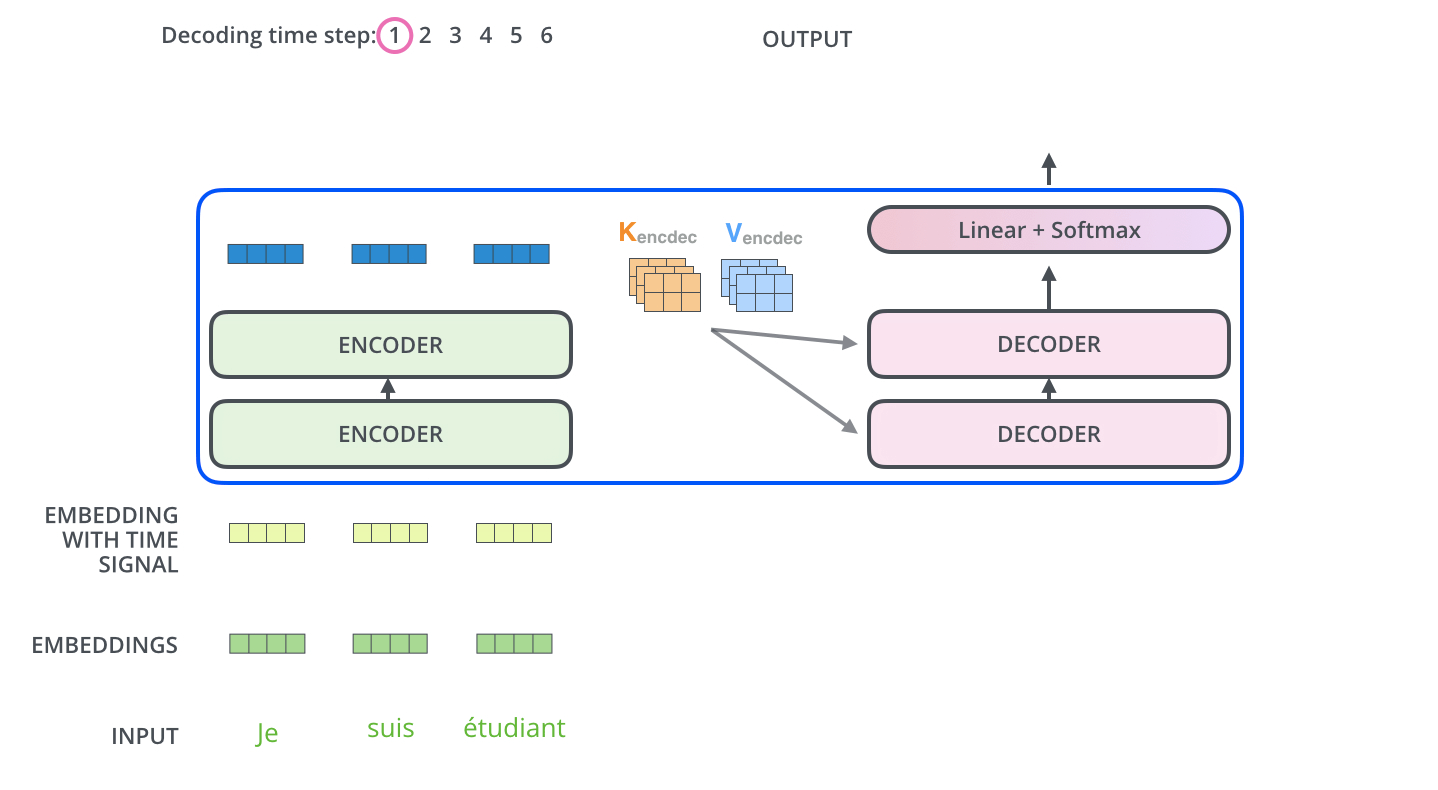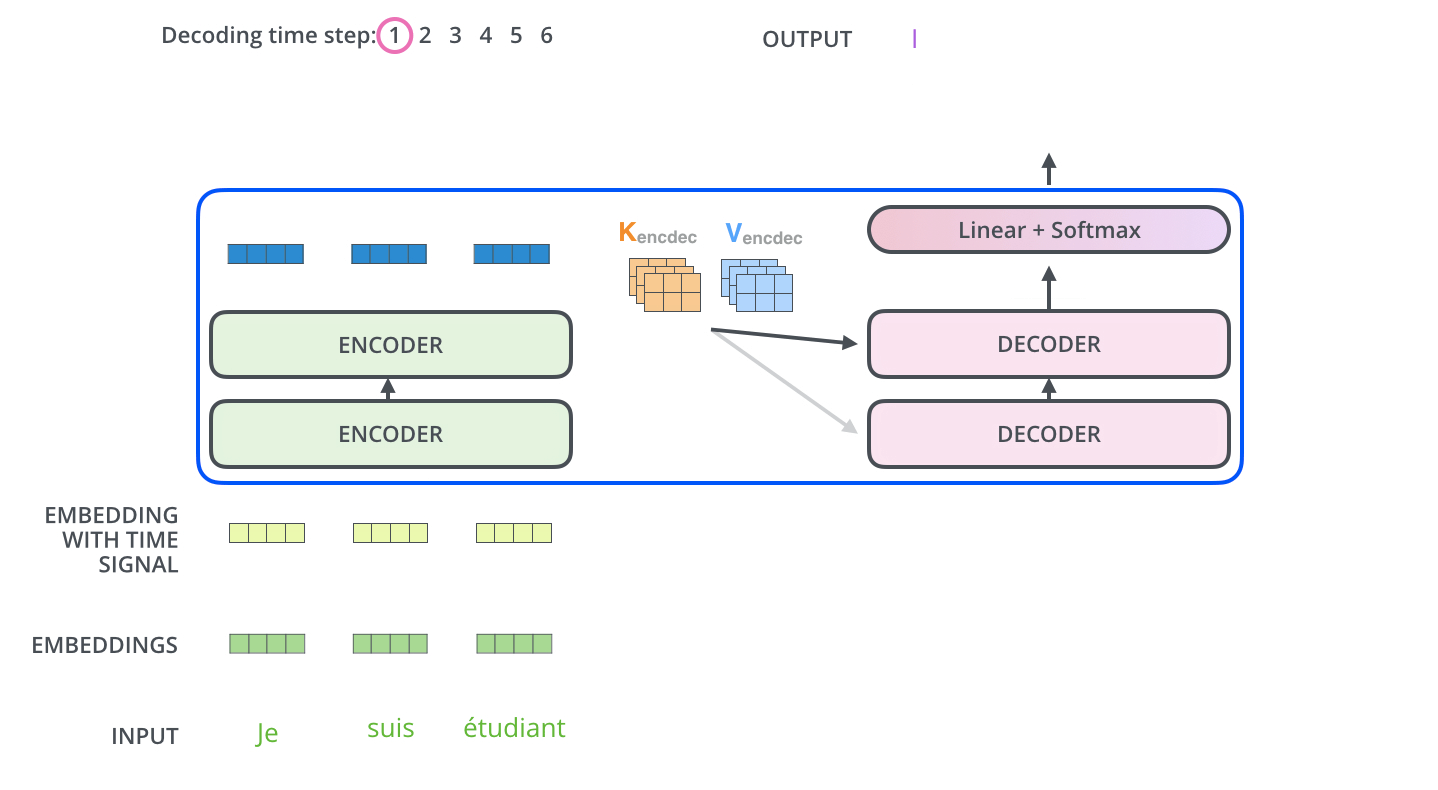
4. Transformer在机器翻译中的应用

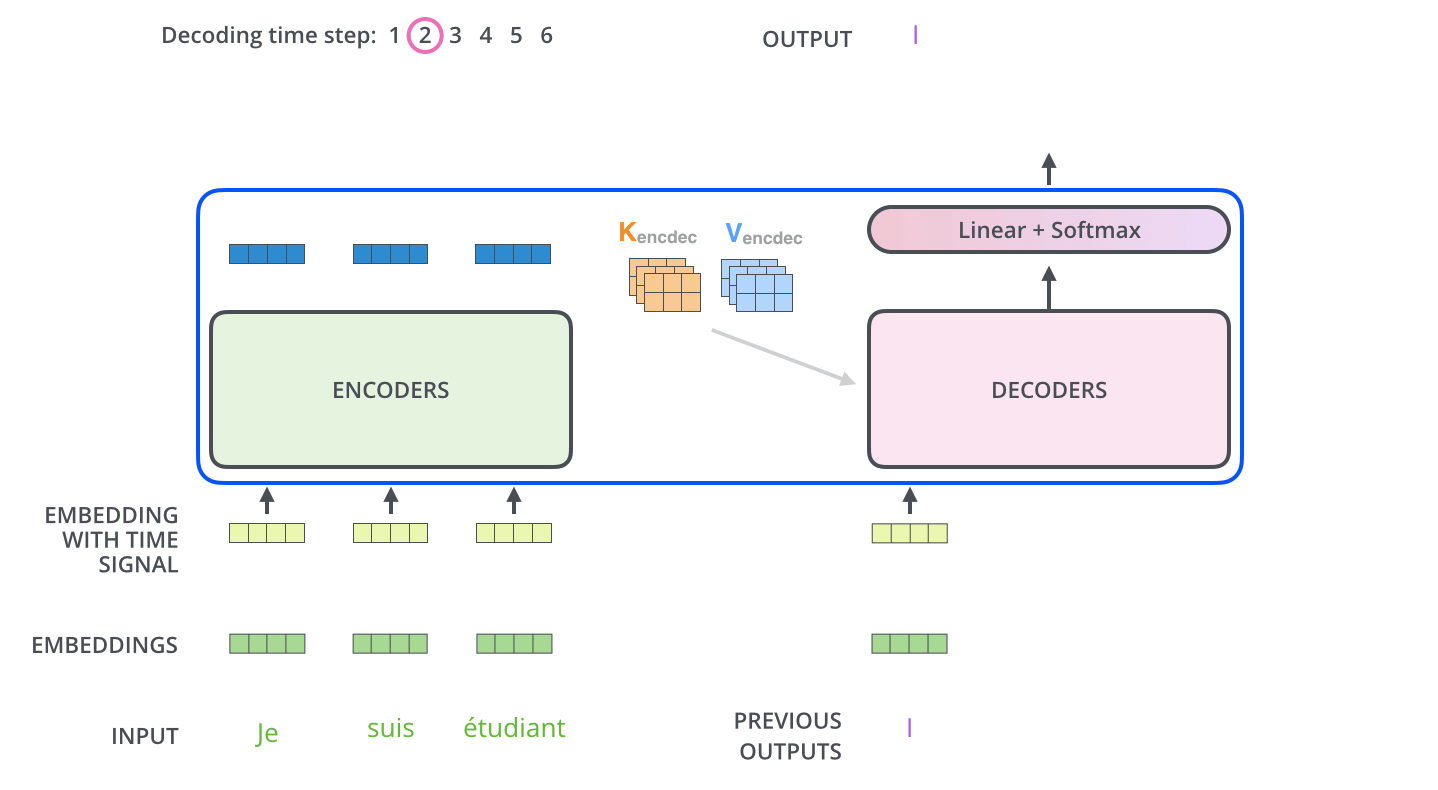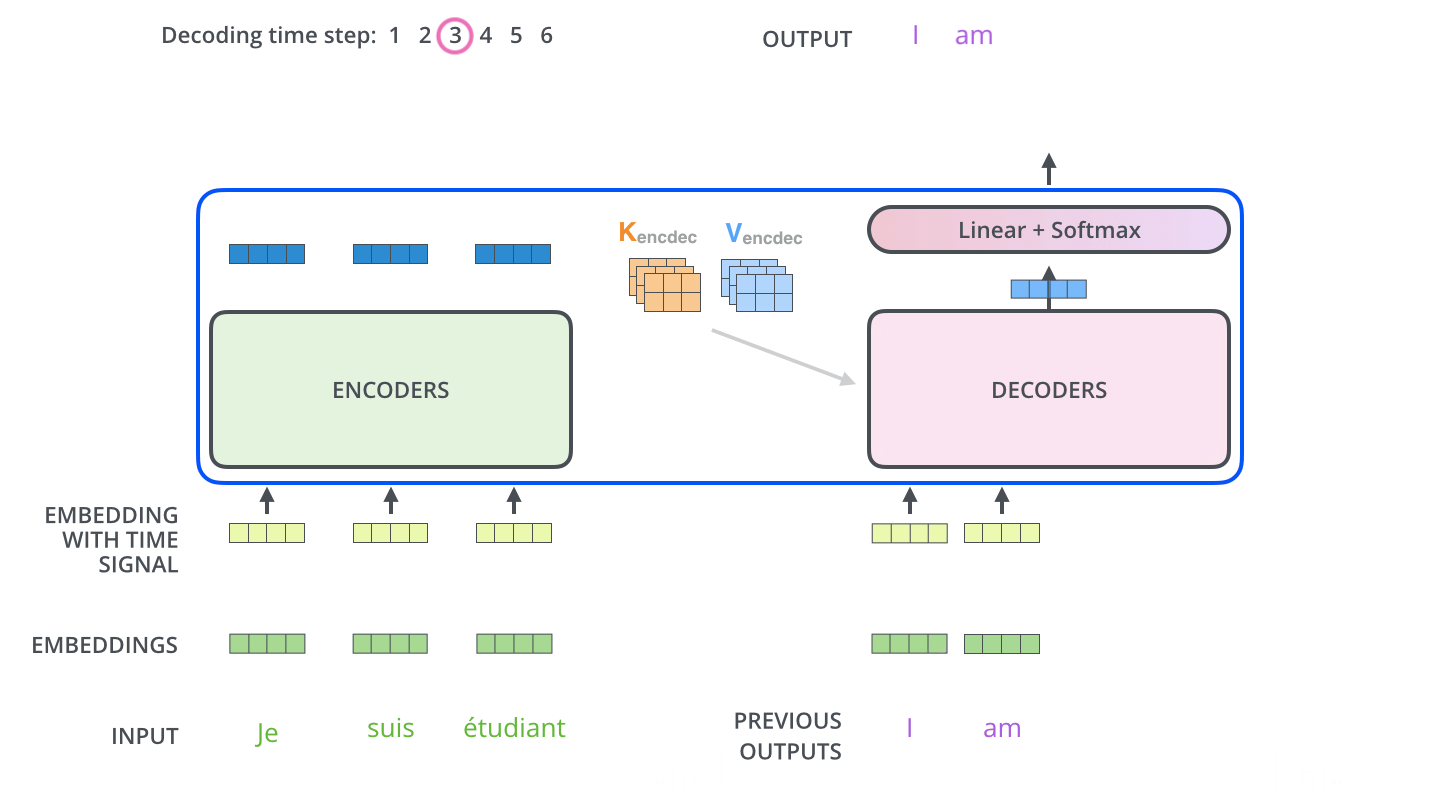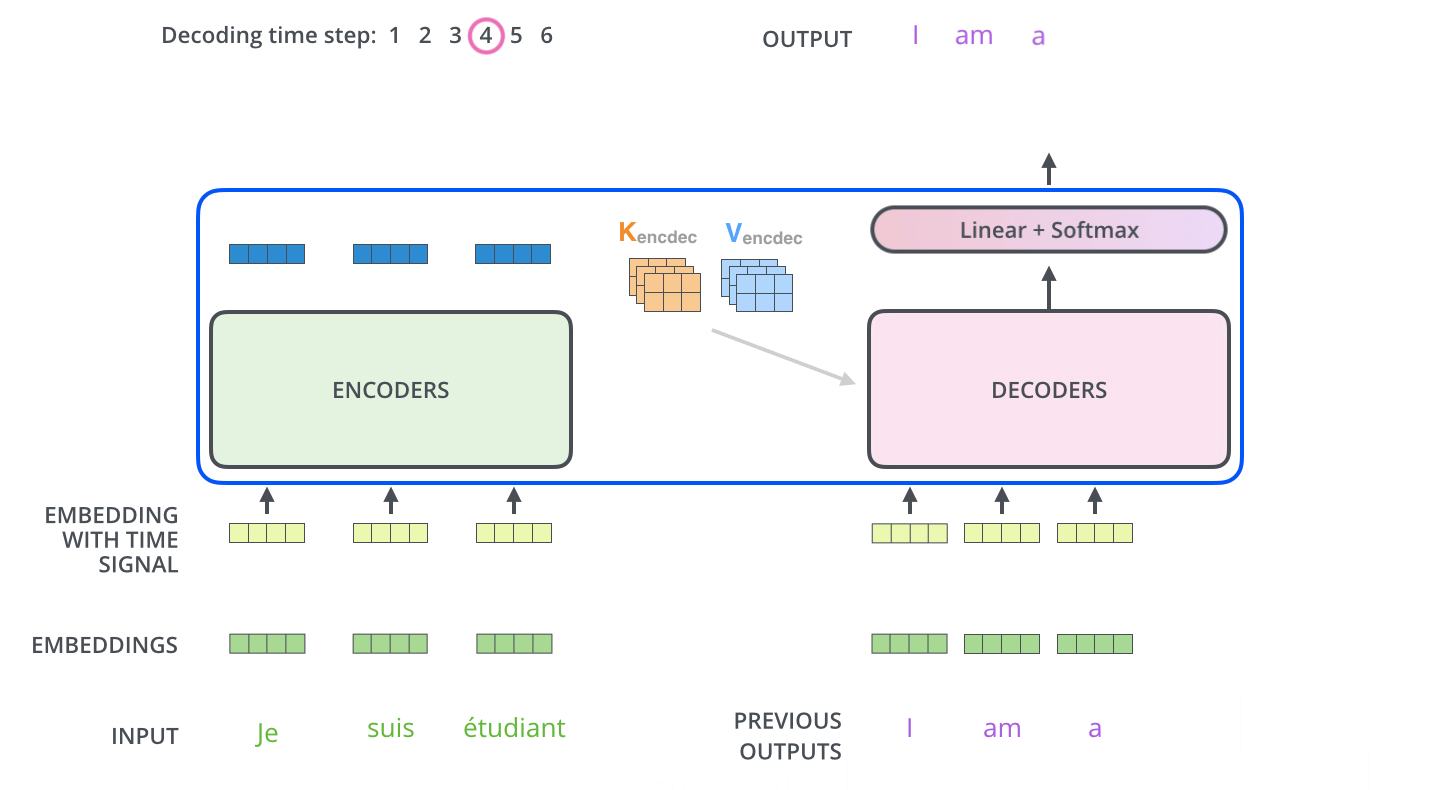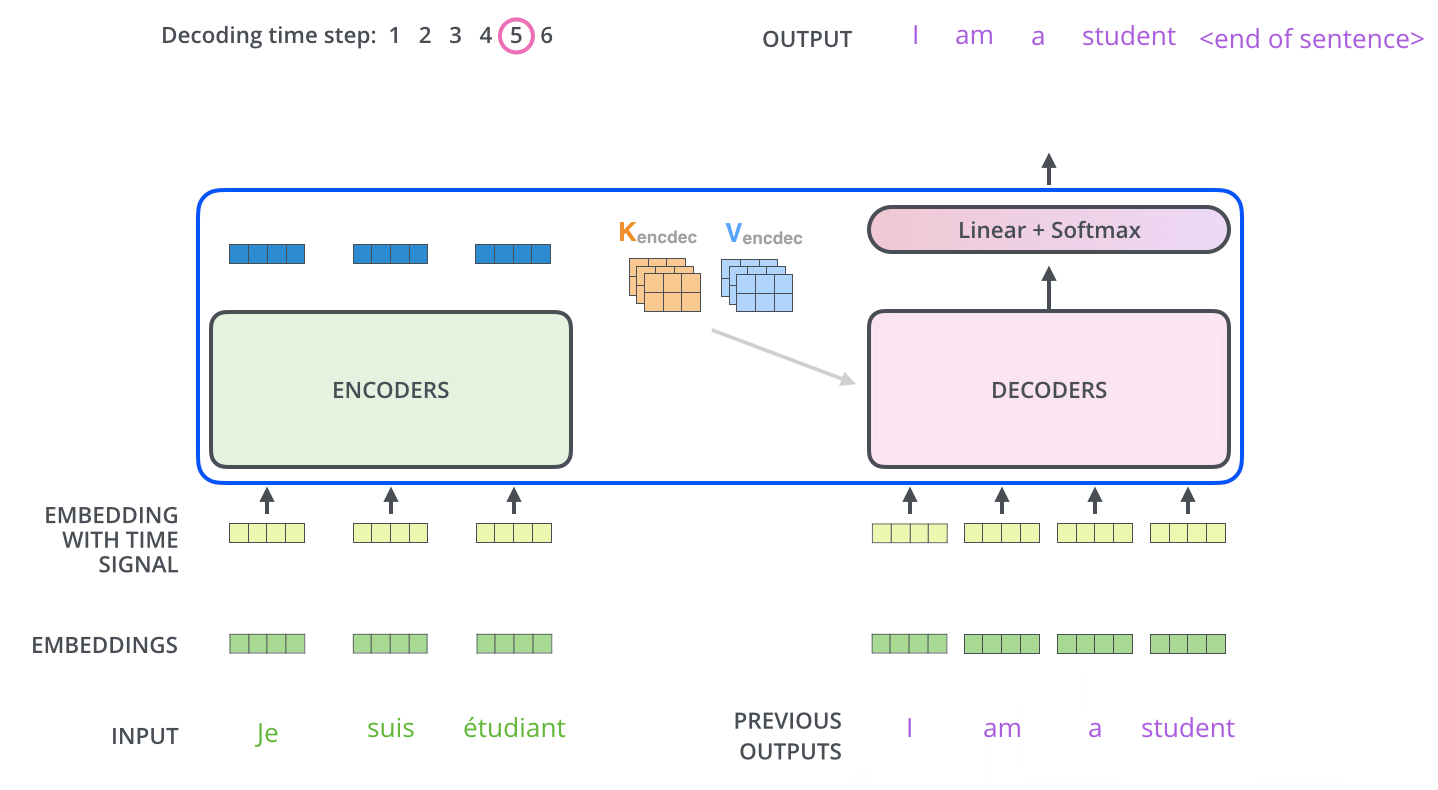
5. 关于K, Q, V的讨论

到这里我们关于整个Transformer的介绍就结束了，我们先从整体上介绍了Transformer也是一个基于encoder-decoder的结构，然后抽丝剥茧般的一层一层的剥开模型，看看它的每一部分到底长什么样子，然后我们了解了每个零件之后又重新把每个零件组装回去。但是还是有两个问题我们可以再细致的讨论一下的，比如为什么需要$V$？为什么$K, Q$使用不同的权重获得？

5.1 我们为什么需要V？

注意力权重矩阵可以表示序列中任意两个元素的相似性，但是不能用来表示原始的序列，因为它缺少了词向量。注意力的作用是给原始序列中的不同位置上的元素以不同的权重，这样可以更好的获取到这个句子中哪一部分重要哪一部分不那么重要，或者说对于句子中的某个词来说，哪个词对它更有依赖关系，哪些词跟它关系没那么密切。所以说，注意力有两个重要的组成部分，一个是注意力权重，也就是词与词之间的相似性，另一个就是原始的句子序列。从模型结构就可以看出来，$K, Q$是用来计算相似性的，那么$V$其实就是用来表征句子序列特征的。

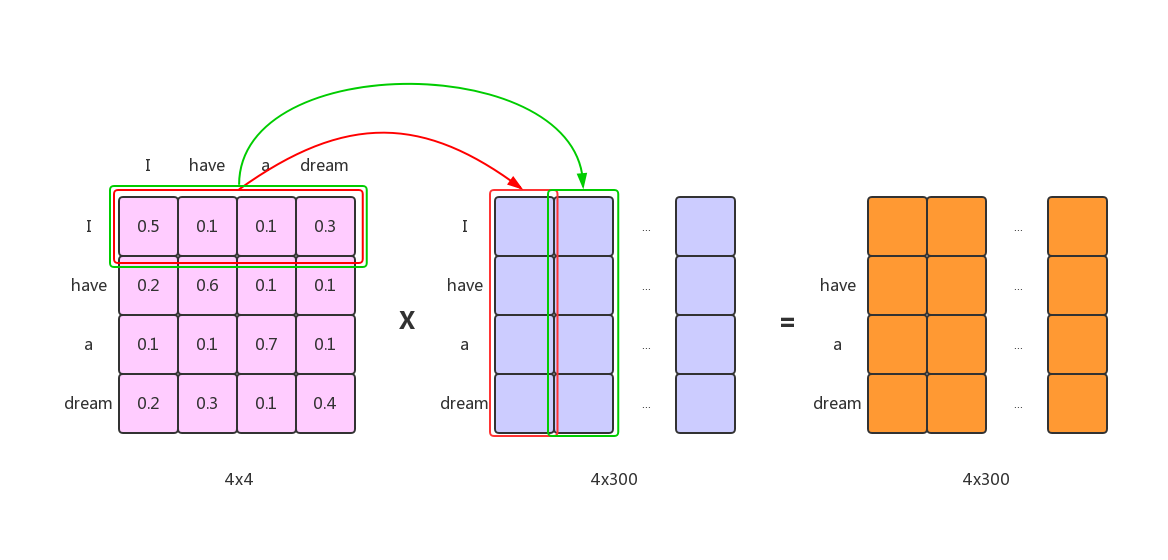
我们可以认为注意力权重矩阵是一个过滤矩阵 ，把更多的注意力给重要的词，给那些不那么重要的词以更少的注意力。

5.2 为什么使用两个不同的权重获得K, Q?

另一个问题就是，我们为什么要用两个不同的矩阵来获得$K, Q$？换句话说，就是我们为什么要用两个不同的矩阵来计算注意力呢？

正如我们前面所说的，注意力实际上是在计算两个词的相似度，如果使用相同的矩阵的话那就相当于计算自己与自己的相似度了，最后我们会得到一个对称矩阵，这样最后的模型的泛化性会大打折扣。

5.3 Transformer是如何实现All You Need的？

回顾一下前一篇文章，我们介绍了各种各样的注意力机制：

用于seq2seq的注意力机制
用于多语义理解的多维注意力机制
用于文本分类和语法纠正的层级注意力机制
用于阅读理解的基于记忆力的注意力机制
用于语言模型的自注意力机制
用于排序的指针网络
其他基于特定任务的注意力机制等等

而Transformer本身就是基于encoder-decoder的结构，由于才用了Multi-Head这种类似多维度注意力机制，所以也能在多维度理解语义，另外由于本身是完全基于注意力的网络所以类层级注意力和类指针网络的的特性应该是Transformer的内秉属性。最后重要的两点：自注意力和基于记忆力的注意力机制在Transformer中表现尤为明显。所以说Transformer可以说是注意力机制的集大成者。

6. 代码实现（Pytorch）

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time
from torch.autograd import Variable


class EncoderDecoder(nn.Module):
    """
    A standard Encoder-Decoder architecture. Base for this and many 
    other models.
    """
    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.generator = generator
        
    def forward(self, src, tgt, src_mask, tgt_mask):
        "Take in and process masked src and target sequences."
        return self.decode(self.encode(src, src_mask), src_mask,
                            tgt, tgt_mask)
    
    def encode(self, src, src_mask):
        return self.encoder(self.src_embed(src), src_mask)
    
    def decode(self, memory, src_mask, tgt, tgt_mask):
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
    
 
class Generator(nn.Module):
    "Define standard linear + softmax generation step."
    def __init__(self, d_model, vocab):
        super(Generator, self).__init__()
        self.proj = nn.Linear(d_model, vocab)

    def forward(self, x):
        return F.log_softmax(self.proj(x), dim=-1)
    
    
def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])


class Encoder(nn.Module):
    "Core encoder is a stack of N layers"
    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, mask):
        "Pass the input (and mask) through each layer in turn."
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)
    
    
class LayerNorm(nn.Module):
    "Construct a layernorm module (See citation for details)."
    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
    
    
class SublayerConnection(nn.Module):
    """
    A residual connection followed by a layer norm.
    Note for code simplicity the norm is first as opposed to last.
    """
    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        "Apply residual connection to any sublayer with the same size."
        return x + self.dropout(sublayer(self.norm(x)))
    
    
class EncoderLayer(nn.Module):
    "Encoder is made up of self-attn and feed forward (defined below)"
    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size

    def forward(self, x, mask):
        "Follow Figure 1 (left) for connections."
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)
    
    
class Decoder(nn.Module):
    "Generic N layer decoder with masking."
    def __init__(self, layer, N):
        super(Decoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, memory, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)
    
    
class DecoderLayer(nn.Module):
    "Decoder is made of self-attn, src-attn, and feed forward (defined below)"
    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 3)
 
    def forward(self, x, memory, src_mask, tgt_mask):
        "Follow Figure 1 (right) for connections."
        m = memory
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        return self.sublayer[2](x, self.feed_forward)
    
    
def subsequent_mask(size):
    "Mask out subsequent positions."
    attn_shape = (1, size, size)
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
    return torch.from_numpy(subsequent_mask) == 0


def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) \
             / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn


class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        "Implements Figure 2"
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d_k 
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        
        # 2) Apply attention on all the projected vectors in batch. 
        x, self.attn = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)
        
        # 3) "Concat" using a view and apply a final linear. 
        x = x.transpose(1, 2).contiguous() \
             .view(nbatches, -1, self.h * self.d_k)
        return self.linears[-1](x)
    
    
class PositionwiseFeedForward(nn.Module):
    "Implements FFN equation."
    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(F.relu(self.w_1(x))))
    
    
class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)
    
    
class PositionalEncoding(nn.Module):
    "Implement the PE function."
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        
        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
        
    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], 
                         requires_grad=False)
        return self.dropout(x)
    
    
def make_model(src_vocab, tgt_vocab, N=6, 
               d_model=512, d_ff=2048, h=8, dropout=0.1):
    "Helper: Construct a model from hyperparameters."
    c = copy.deepcopy
    attn = MultiHeadedAttention(h, d_model)
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    position = PositionalEncoding(d_model, dropout)
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        Decoder(DecoderLayer(d_model, c(attn), c(attn), 
                             c(ff), dropout), N),
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        Generator(d_model, tgt_vocab))
    
    # This was important from their code. 
    # Initialize parameters with Glorot / fan_avg.
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform(p)
    return model

Rogerspy's Home