NLP中的注意力机制简介（一）

1. 简介

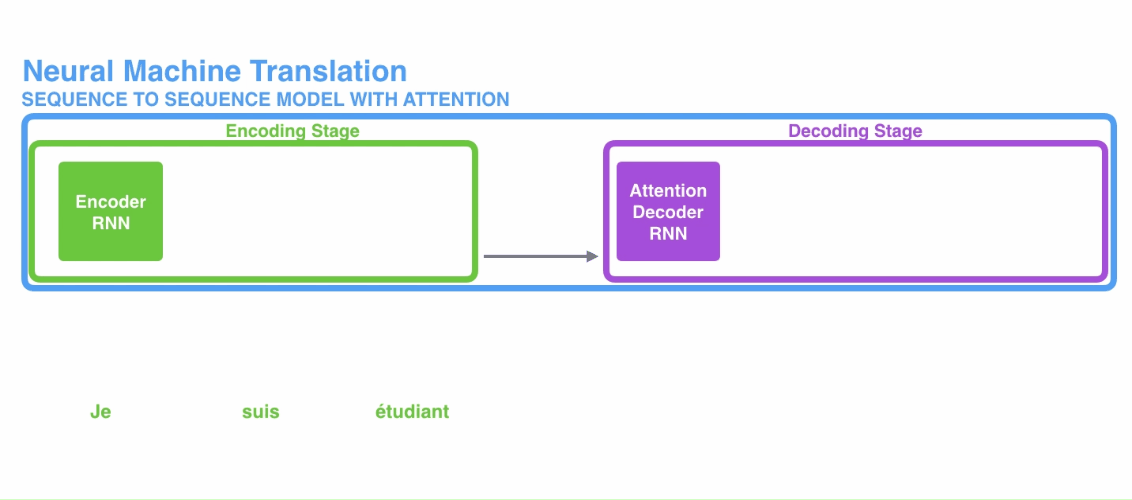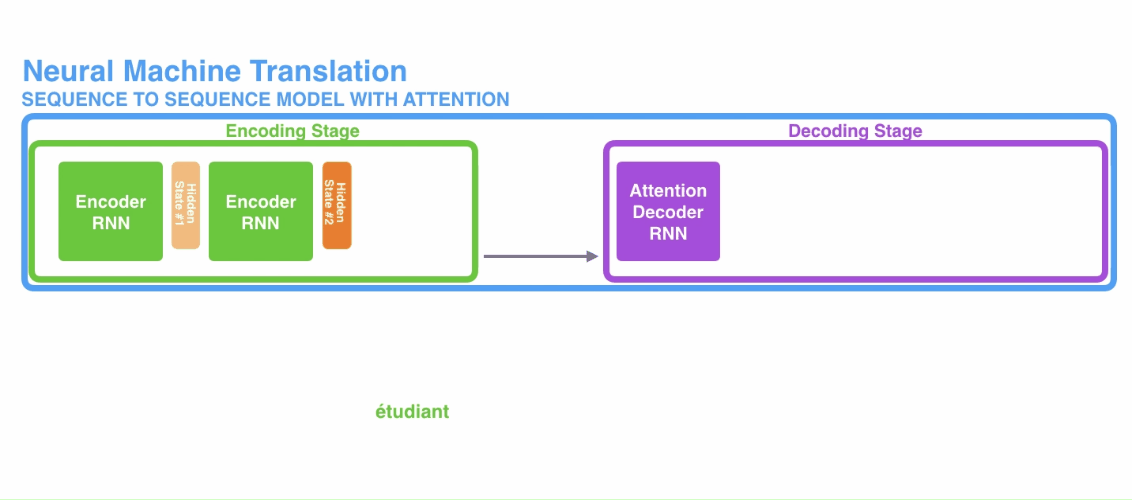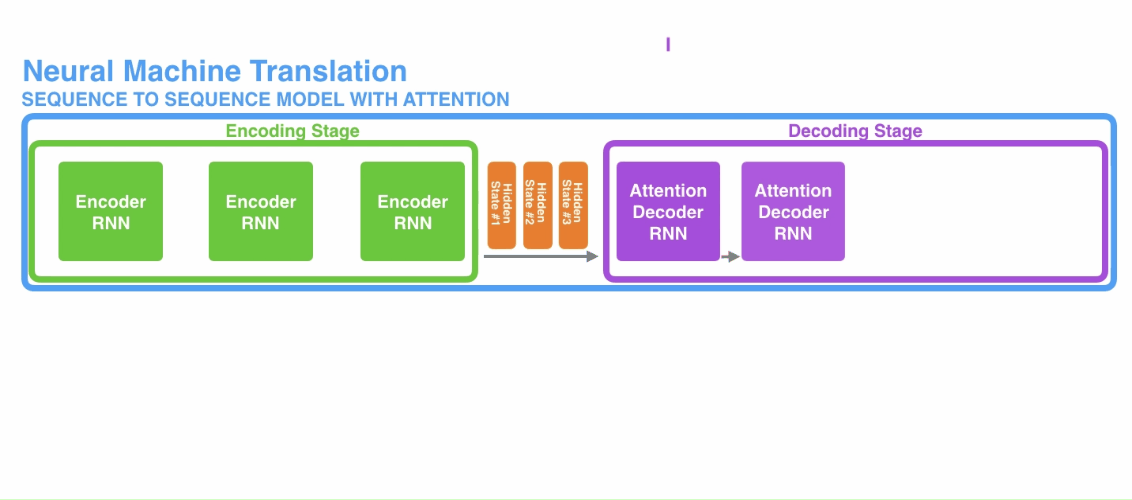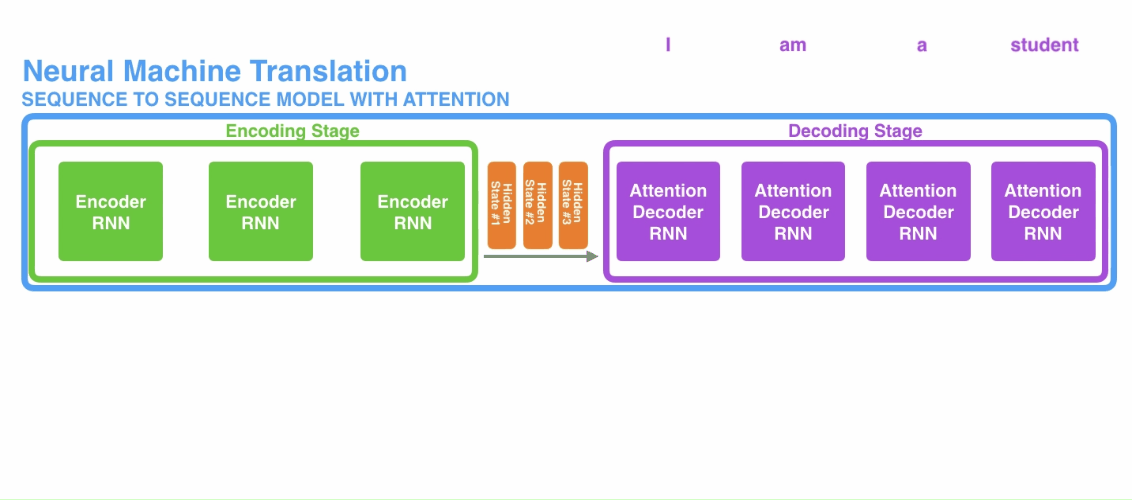
传统的注意力机制是与encoder-decoder架构相结合的，其中编码器和解码器都是RNN。首先是一段文本序列输入到编码器当中，然后将编码器的最后一个隐状态单元作为解码器的初始状态，然后一个接一个地产生目标序列，如下所示：

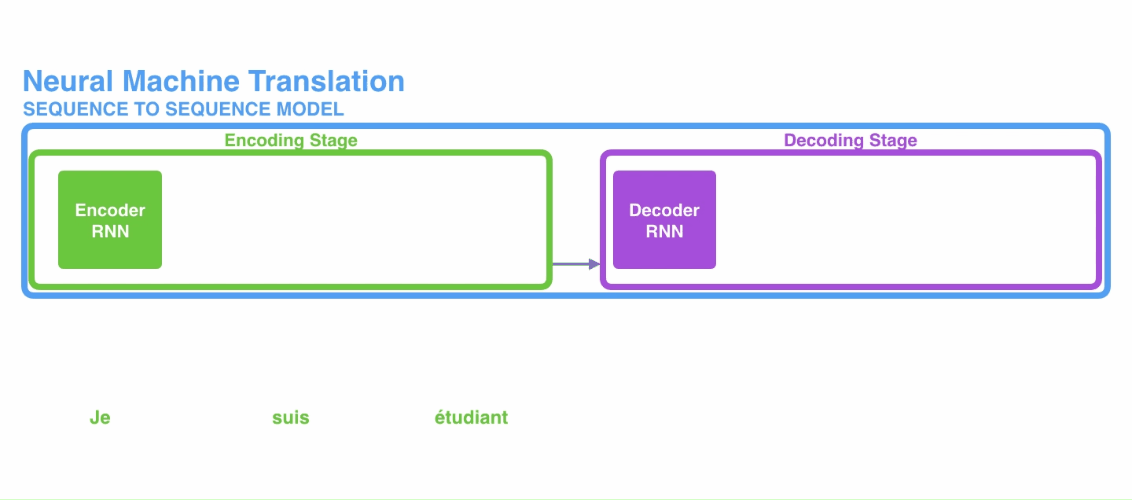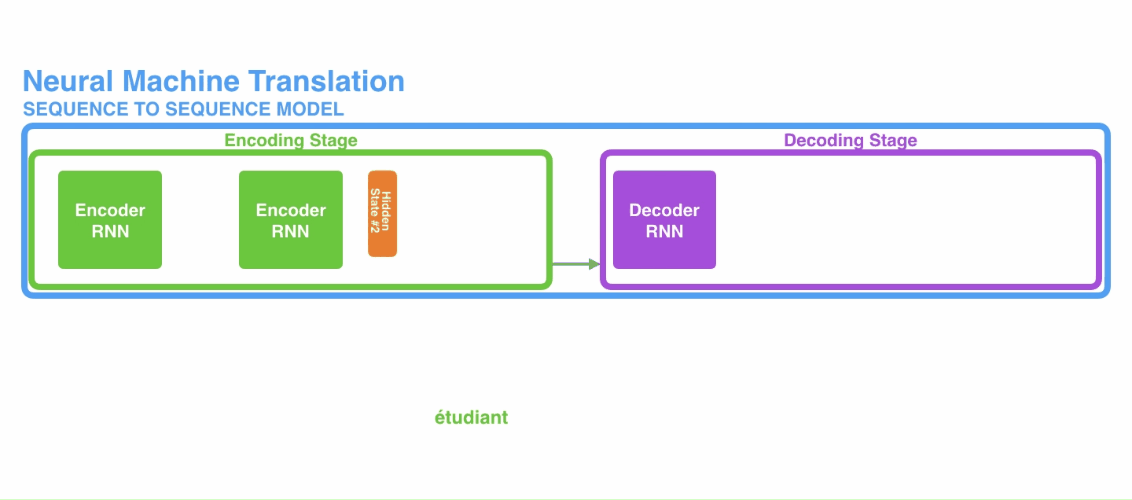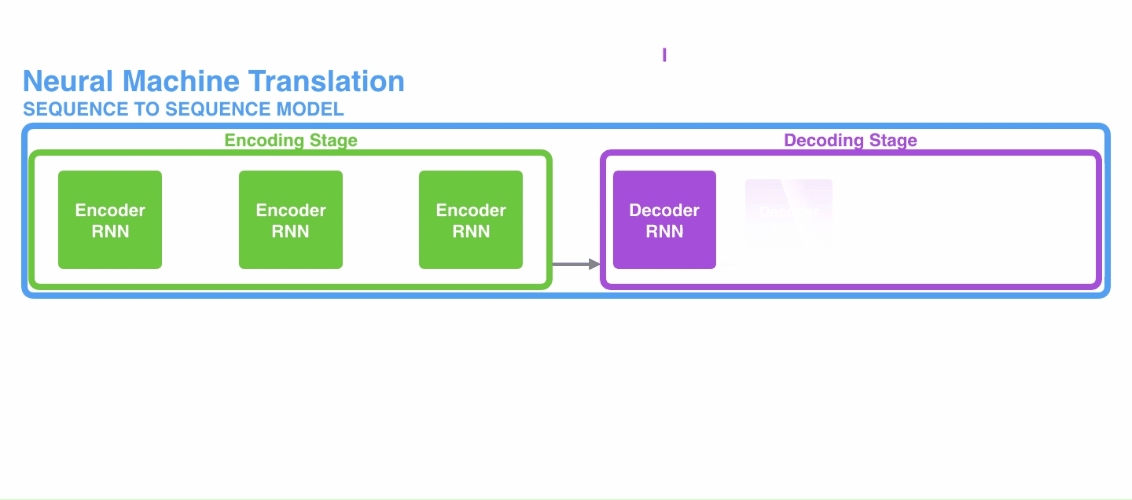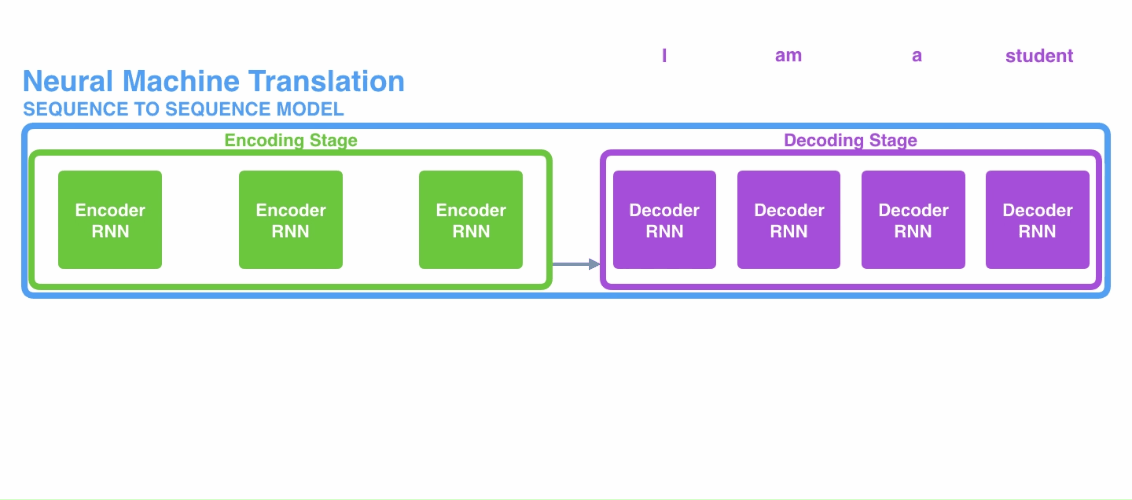
encoder-decoder结构在机器翻译任务中被广泛使用，尽管这种方法相较之前的统计翻译方法对翻译效果有很大的提升，但是这种基于RNN的结构也存在两个非常严重的问题：

1. RNN是可遗忘的（forgetful），这就意味着随着信息的传递，在经历了多个时间步长之后，旧的信息可能会丢失；（长程依赖问题）
2. 在解码过程中没有利用词对齐信息，也就是说在产生目标序列的过程中每产生一个词是基于整个源序列的信息的，由于注意力分散，所以在产生目标序列的过程中也容易出错。（注意力分散问题）

为了解决以上两个问题， Bahdanau et al., 2014和 Luong et al., 2015提出了注意力机制。论文中仍然使用基于RNN的encoder-decoder结构，但是在解码过程中每个时间步长都会计算注意力得分，然后再生成该隐状态下对应的输出。下面我们以seq2seq with attention模型为例，介绍传统注意力机制过程：

加入了注意力机制的encoder-decoder模型与标准的encoder-encoder有两点区别：

1. 传入decoder的数据不再是单纯的encoder的最后一个隐状态，而是encoder的所有隐状态；
2. decoder在产生输出之前还会有额外的计算，用于确定当前decoder的隐状态应该对应到哪个encoder的隐状态，这样相当于集中注意力来产生与之对应的输出，这也是注意力机制得名的由来。

注意力得分的计算过程如下所示：

1. 准备好输入到decoder的所有encoder隐状态$\mathbf{h}_1,\mathbf{h}_2,\mathbf{h}_3$；
2. 对每一个隐状态给定一个得分；
3. 对得分使用softmax进行归一化，即为注意力得分；
4. 使用注意力得分和每个decoder隐状态相乘，得到隐状态在当前decoder下的重要性；
5. 最后对加权后的encoder隐状态进行求和，求和后的隐状态即相当于原始encoder-decoder中的单一隐状态。

以上步骤在decoder中的每一个时间步长上都进行一次计算，仍然以翻译模型为例，对整个过程进行简单的介绍：

1. 首先是encoder中对输入的句子序列进行编码，得到$h_1, h_2, h_3$三个隐状态待用；
2. 第一个decoder单元接收到源序列中的终止符开始进行解码，decoder单元首先初始化一个隐状态权重，此时与接收到的源序列终止符相互作用，但并不产生输出，而是产生一个新的隐状态$\mathbf{h}_4$；
3. 利用上述计算注意力得分的方法对$\mathbf{h}_1,\mathbf{h}_2,\mathbf{h}_3$，进行注意力计算得到$C_4$；
4. 将$C_4$和$\mathbf{h}_4$进行拼接得到一个新的向量；
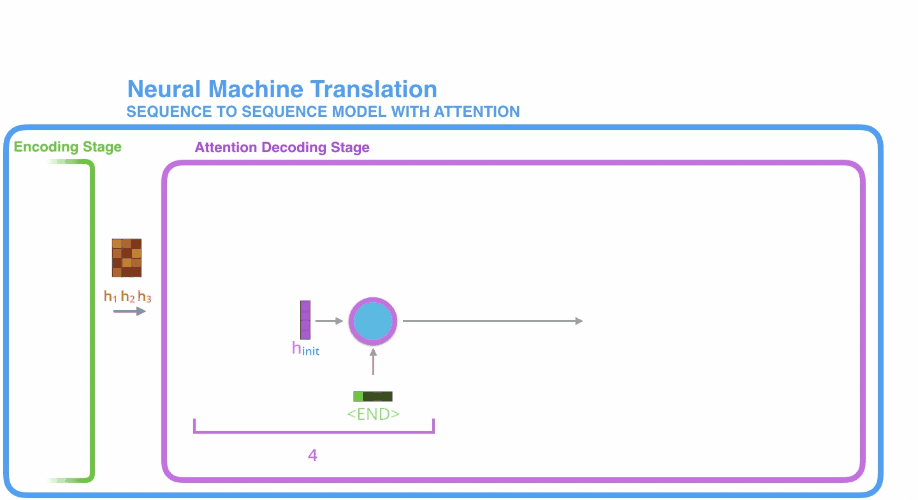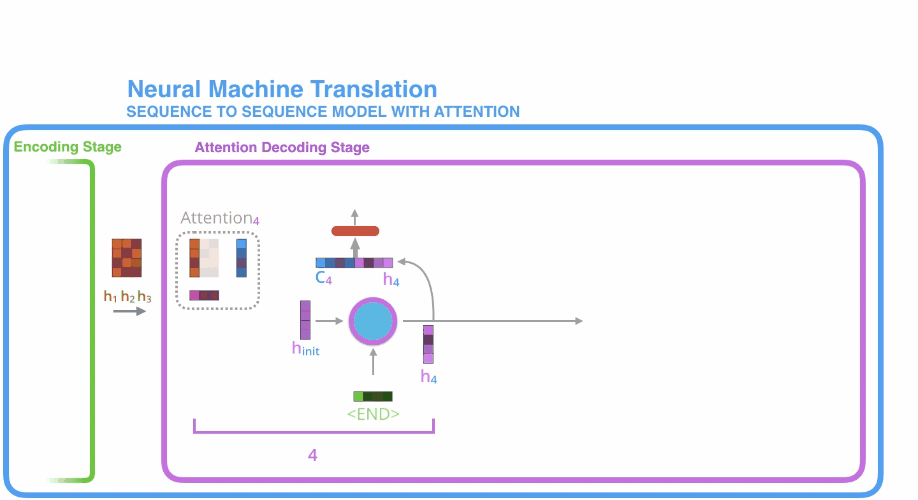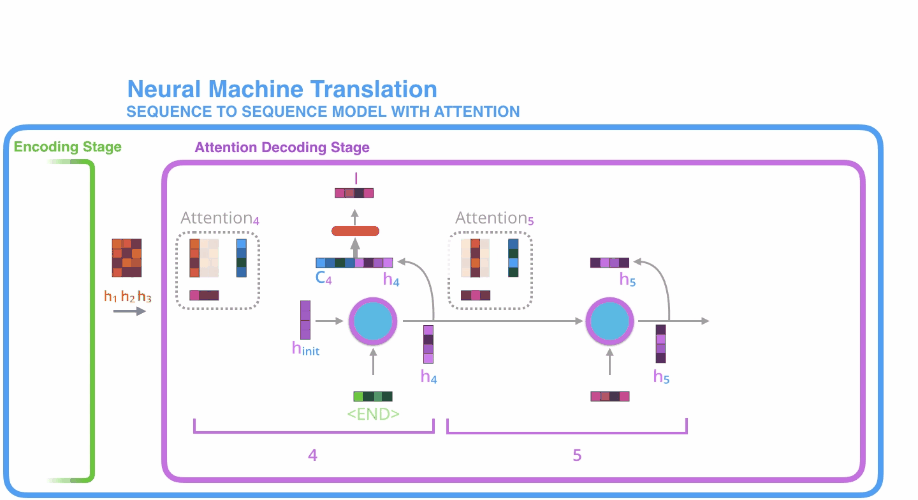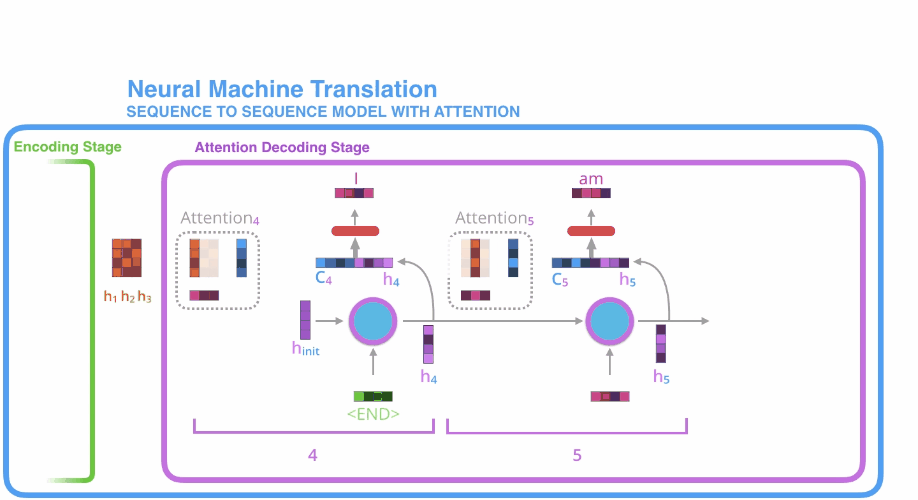
5. 将新向量传入到一个全连接层，全连接层的输出则是第一个decoder的输出，即目标序列的第一个元素；
6. 将上述$\mathbf{h}_4$隐状态作为第二个decoder单元的初始隐状态，第一个decoder的输出向量（即全连接层的输出）作为第二个decoder的输入，再次重复上面的步骤$3-5$。

从上面的过程可以看出，注意力机制的核心点在于注意力权重的计算，下面呢我们对这个计算过程进行公式化描述：

$$e_{ji} = a(\mathbf{h}_i^{in}, \mathbf{h}_j^{out})$$ $$\alpha_{ji} = \frac{exp(e_{ji})}{\sum_iexp(e_{ji})}$$ $$\mathbf{c}_j = \sum_i\alpha_{ji}\mathbf{h}_i^{in}$$

其中$\mathbf{h}_i^{in}$表示decoder单元的输入隐状态（即encoder第$i$个隐状态），$\mathbf{h}_j^{out}$表示当前decoder单元的输出，$e_{ji}$表示第$i$个encoder隐藏层对当前decoder单元输出的影响权重（$j$表示第$j$个decoder时间步长，为了方便这里指当前step）,此即为上述注意力全忠计算过程中的步骤$2$。公式$(2)$即使用softmax进行权重的归一化，$\alpha_{ji}$就是归一化后的注意力权重，即为注意力权重计算过程步骤$3$。公式$(3)$表示的就是注意力权重计算过程步骤$4-5$。

得到注意力权重以后，与当前的decoder隐状态$h_j$和输入$y_{j-1}$结合最终输出目标元素（注意：这里当前decoder的输入是上一个decoder的输出，可参考前面的seq2seq模型的整个过程的介绍。）

$$\mathbf{y}_j = f_y(\mathbf{h}_j^{out}, \mathbf{y}_{j-1},\mathbf{c}_j)$$ $$\mathbf{h}_{j+1}^{out} = f_h(\mathbf{h}_j^{out}, \mathbf{y}_j)$$

其中$f_y$和$f_h$表示RNN的输出层和隐状态层。

将上述计算过程对每一个RNN时间步长进行重复计算就能解决最开始我们提出的单纯基于RNN的encoder-decoder模型所带来的问题：

1. 对于长程依赖问题，由于计算注意力过程每次都会通过输入序列的隐状态来计算，因此$\mathbf{c}_j$不会受到源序列长度的影响；
2. 对于注意力分散的问题，由于我们在每一次进行decode的时候都会进行注意力加权，注意力只会集中在对当前影响较大的部分序列上，而不是把注意力分散到整个序列中，因此有效的解决了注意力分散的问题。

注意力机制自从被提出来以后，在机器翻译领域取得了非常打的成功，随后注意力机制被广泛应用于NLP各个领域中，并且为了解决不同领域中各种问题，注意力机制也出现了各种各样的变种，下图总结了最近几年关于注意力机制的一些比较重要的研究。

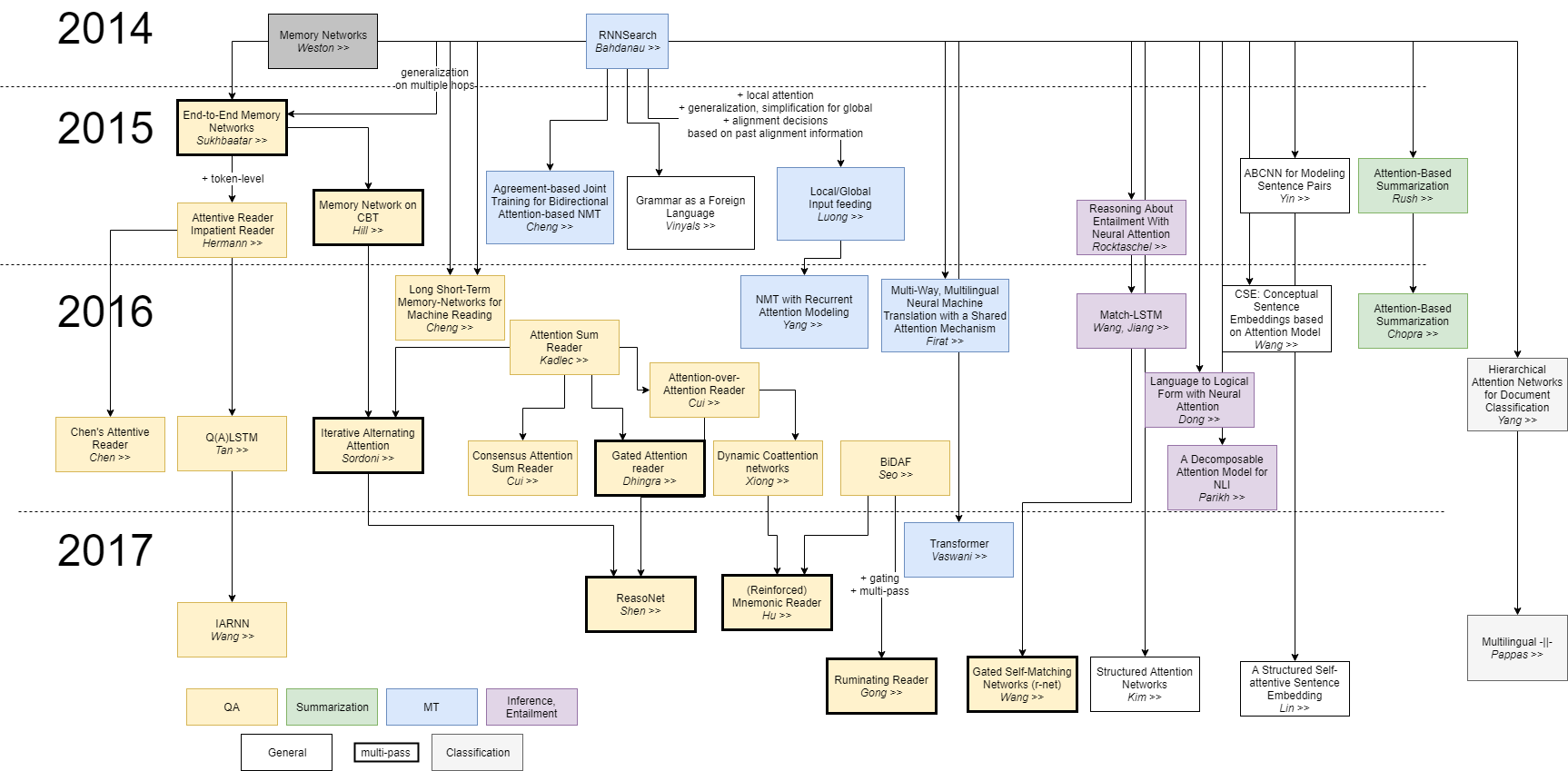
下面我们就介绍一些比较重要的注意力模型。

2. 注意力模型的基本形式

前面我们介绍了注意力机制在神经机器翻译中的应用，为了更一般化、形式化注意力机制，首先定义$V=\{\mathbf{v}_i\} \in \mathbb{R}^{n\times d_v}$，其中$\mathbf{v}_i$表示序列元素对应的向量（这里实际上应该是经过编码后的隐状态向量即前文所说的$\mathbf{h}_i$），重写之前的注意力模型：

$$e_i = a(\mathbf{v}_i, \mathbf{u})$$ $$\alpha_i = \frac{exp(e_i)}{\sum_i exp(e_i)}$$ $$c = \sum \alpha_i \mathbf{v}_i$$

其中$\mathbf{u} \in \mathbb{R}^{d_v}$表示序列$\{\mathbf{v}_i\}$对应的输出（pattern vector）， 而$e_i$则表示序列$\{\mathbf{v}_i\}$中第$i$个元素对输出的影响，多数情况下$d_u=d_v=d$，而$a(\cdot)$函数（又叫Alignment score function）通常有一下几种选择：

Name	Alignment score function $a(\cdot )$	Notes	Citation
Content-base	$a(\mathbf{v}_i, \mathbf{u})=cosine([\mathbf{v}_i, \mathbf{u}])$	—	Graves2014
Additive	$a(\mathbf{v}_i, \mathbf{u}) = \mathbf{w}_2^{T}tanh(W_1[\mathbf{v}_i;\mathbf{u}])$	—	Bahdanau2015
Location-base	$\alpha_i=softmax(W\mathbf{u})$	只依赖目标输出，直接计算注意力权重	Luong2015
General	$ a(\mathbf{v}_i, \mathbf{u}) = \mathbf{u}^TW\mathbf{v}_i$	—	Luong2015
Dot-product	$a(\mathbf{v}_i, \mathbf{u}) = \mathbf{u}^T\mathbf{v}_i$	—	Luong2015
Scaled Dot-product	$a(\mathbf{v}_i, \mathbf{u}) = \frac{\mathbf{u}^T\mathbf{v}_i}{\sqrt{n}}$	其中$n$是$\mathbf{v}_i$的向量维度	Vaswani2017

以Content-base为例，计算出$e_i$在进行归一化，实际上可以认为这是一个相似性计算（类似$cos(\cdot)$）的操作，也就是说这里是在计算$\mathbf{v}_i$与输出之间的相似性。

为了避免混淆，我们先解释一下本文所采用的符号：

• 小写符号表示标量，如$e_i$;
• 小写加粗符号表示向量， 如$\mathbf{v}_i$;
• 大写符号表示矩阵， 如$W$；
• 大写加粗符号表示张量，如$\mathbf{W}$；
• $W, b$默认为待学习的权重矩阵和偏置

3. 注意力机制的变种

前面我们讨论了注意力机制的基本形式，由于其简单且有效使得注意力机制在NLP领域被广泛使用，但是通常在一些复杂性况下，这种简单形式的注意力机制仍然不够强大。随着注意力机制在不同场景下的应用，各种各样与之相关的注意力机制被提出来，总结起来可以概括为：基础注意力（Basic Attention），多维注意力（Multi-dimensional Attention），层级注意力（Hierarchical Attention），自注意力（Self-Attention），基于记忆的注意力（Memory-based Attention），指针网络（Pointer Network），特定任务下的注意力（Task-specific Attention）。

注意我们是根据不同的NLP任务应用场景对注意力机制进行分类的，在一些论文或者博客中通常见到的注意力模型分类将注意力分成soft attention, hard attention, global attention, local attention, self-attention等，与本文的分法不太相同，这是因为分类的依据不同。这里对这种分类方法的注意力机制做简单的介绍：

soft/hard attention的区别类似于word embedding和one-hot的区别。soft attention的优势在于注意力平滑可微分，也就是说可以利用梯度下降进行权重更新，缺点就是如果输入较大（输入序列过长）比较消耗计算资源。hard attention的优势就是计算资源消耗少，但缺点就是不能微分，在进行权重更新的时候需要比较复杂的技术来处理这个问题。

global attention 类似于soft attention将整个序列的信息融合进一个向量中，local attention类似于hard attention，它是在一个选定的窗口内进行soft attention，而在窗口之外仍然是hard attention。在特定任务下的注意力机制中我们会介绍一个local attention在机器翻译中的应用。

表1总结了不同注意力模型各自的特点：

注意力机制类型	特点
Basic Attention	从一个序列中抽取出重要的元素
Multi-dimensional Attention	获得元素之间的多种操作类型
Hierarchical Attention	抽取全局和局部的重要信息
Self-Attention	抽取序列中隐含的上下文信息
Memory-based Attention	获取NLP任务中的隐藏的依赖关系
Pointer Network	对输入序列进行排序
Task-specific Attention	获取特定任务中的重要信息

3.1 多维注意力机制

前面我们介绍的基础注意力模型可以认为是一维的注意力机制（1D-attention），因为对于序列$V=\{\mathbf{v}_i\}$中的每一个元素计算出来的注意力权重$\alpha_i$都是一个标量，即$V=\{\mathbf{v}_i\}$对应的注意力权重为$\mathbf{\alpha}=\{\alpha_i\} \in \mathbb{R}^n$。但是在需要提取多种信息表示的情况下1D-attention就显得无能为力了，比如：

Fish Burger is the best dish it tastes fresh.

这样一句很简单的话，我们可以有不同的理解方式：

1. 晚餐之中哪道菜是最好的？
2. 晚餐中Fish Burger这道菜和其他菜比起来怎么样？

对于第一个理解方式，那么注意力应该在Fish Burger；而对于第二种理解方式，注意力应该在the best上面。也就是说针对不同语境（representation space），同一句话的注意力重点也是不同的。因此，我们需要多个注意力来处理这类情况，即所谓的Multi-dimensional attention。

最简单的方式就是多个1D-attention堆积成一个Multi-dimensional attention。例如Wang et al., 2017提出的2D-attention：给定一个输入序列$V=\{\mathbf{v}_i\}$，两个representation space $U = \{\mathbf{u}^a, \mathbf{u}^p\}$，权重张量$\mathbf{W}=\{W_a, W_p\}$，注意力权重的计算变为：

$$\mathbf{e}_i = tanh([\mathbf{v}_i^TW_a\mathbf{u}^a:\mathbf{v}_i^TW_p\mathbf{u}^p])$$

其中$[:]$表示两个向量的拼接，$E = \{\mathbf{e}_i\}$， 经过softmax归一化之后得到注意力矩阵$\Lambda = \{\alpha_i\}$。结果如图所示：

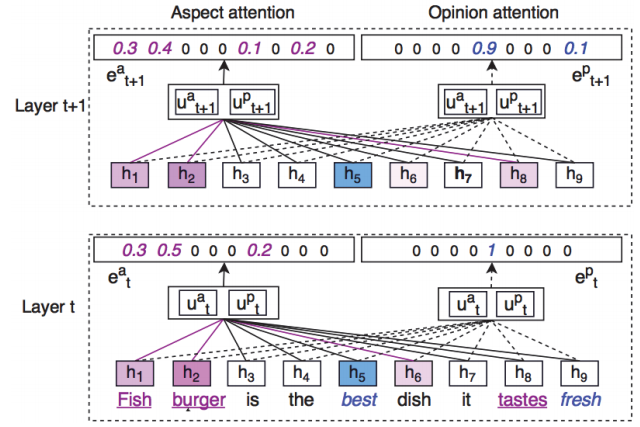
Aspect attention和Opinion attention表示两个representation space，Aspect attention能把注意力集中在Fish Burger上，而Opinion attention能把注意力集中在best上，这样就解决了上面提到的问题。

然而这种多维注意力机制存在一个问题：

如果每一维注意力都有相似的注意力，那么最后得到的信息会存在信息冗余的问题。

针对这个问题Lin et al. 2017提出一种惩罚机制，即

$$P = \|(\Lambda \Lambda^T-I)\|_F^2$$

其中$\Lambda$ 表示注意力矩阵，$I$表示单位矩阵，$|\cdot|_F$表示Frobenius范数。类似于添加一个$L_2$正则项，这个惩罚项会乘以一个系数（超参数）然后和原始的损失函数一同计算最小化。

下面我们讨论一下这个惩罚项的有效性（原始论文中作者最先考虑的是KL散度，但是在实际测试过程中发现效果并不理想，所以才考虑添加这样一个惩罚项）。

考虑 $\Lambda = \{\alpha_a, \alpha_p\}$，由于$\alpha_a$和$\alpha_p$都经过了softmax，因此$\alpha_a$和$\alpha_p$可以被认为是离散概率分布中的概率质量（probability mass），对于$\Lambda \Lambda^T$矩阵中任意非对角的元素$\alpha_{ij}(i\neq j)$，对应于两个分布的元素级乘积求和：

$$0 \lt \alpha_{ij}=\sum_{k=1}^n\alpha_k^i\alpha_k^j \lt 1$$

其中$\alpha_k^i$和$\alpha_k^j$分别对应$\mathbf{\alpha}_a$和$\mathbf{\alpha}_p$的第$k$个元素。最极端情况下假设$\mathbf{\alpha}_a$和$\mathbf{\alpha}_p$没有任何交叉点，即$\alpha_{ij}=0$，否则$\alpha_{ij} \gt 0$；另一个极端情况是假设$\mathbf{\alpha}_a$和$\mathbf{\alpha}_p$完全相等，即两个注意力全部在同一个词上面，此时$\alpha_{ij}=1$。我们从$\Lambda \Lambda^T$中减去一个单位矩阵，相当于强迫$\Lambda \Lambda^T$的对角元素都约等于1，当$\alpha_{ij}=1(i=j)$时，$\alpha_{ij}=0(i \neq j) $，而我们的目的就是使每个维度上的注意力都不相同，所以我们需要$\alpha_{ij}=0(i \neq j)$，满足第一种极端假设。

实际上我们最小化这个惩罚项的时候是在将注意力矩阵$\Lambda $进行正交化，每一行都与其他行正交，即每一行都与其他行的注意力不同。

3.2 层级注意力机制

3.2.1 自下而上的层级注意力机制（Bottom-up Hierarchical Attention）

下面我们考虑文本分类任务。文本分类可以说是NLP中最基础的任务之一了。文本具有典型的层级结构：

character => word => sentence => document

document的类别取决于构成它的sentence，而sentence的意思又取决于word以及词序，也就是说要想对文本很好的进行分类，需要抓住其中的关键词和关键句子（语序可以通过RNN等网络结构来解决，这里不讨论语序的问题）。

针对这个问题Yang et al., 2016提出了Hierarchical Attention Networks (HAN)，也就是层级注意力神经网络。HAN使用双向GRU网络对序列进行编码。给定一个序列$V_j=\{\mathbf{v}_i\}$表示文档中第$j$个句子，$\mathbf{v}_i$则表示句子中第$i$个词。给定一个序列集$\mathbf{D} = \{V_i\}$表示一篇文档。

• Word Encoder

$$\mathbf{h}_i^{word} = BiGRU(\mathbf{v}_i)$$ $$\mathbf{u}_i^{word} = tanh(W_w\mathbf{h}_i^{word}+b_w)$$

这里encoder编码后的隐状态又经过了一层全连接层进行编码。

• Word Attention

$$e_i^{word} = a(\mathbf{u}_i^{word}, \mathbf{u}_w) = \mathbf{u}_w{^T}\mathbf{u}_i{^{word}}$$ $$\alpha_i^{word} = softmax(e_i^{word})$$ $$\mathbf{s}_i = \sum_t \alpha_i^{word}\mathbf{h}_i^{word}$$

其中$\mathbf{s}_i$表示$V_i$经过编码后的句向量，$t$表示句子长度，$\mathbf{u}_w$是随机初始化的可学习参数。

• Sentence Encoder

$$\mathbf{h}_i^{sent} = BiGRU(\mathbf{s}_i)$$ $$\mathbf{u}_i^{sent} = tanh(W_s\mathbf{h}_i^{sent}+b_s)$$

• Sentence Attention

$$e_i^{sent} = a(\mathbf{u}_i^{sent}, \mathbf{u}_s) = \mathbf{u}_s{^T}\mathbf{u}_s^{sent}$$ $$\alpha_i^{sent} = softmax(e_i^{sent})$$ $$\mathbf{d} = \sum_i \alpha_i^{sent}\mathbf{h}_i^{sent}$$

其中$\mathbf{d}$就是document对应的向量。

3.2.2 自上而下的层级注意力机制（Top-down Hierarchical Attention）

HAN是一种bottom-up类型的层级注意力机制，除此之外还有top-down类型的层级注意力机制，比如Ji et al., 2017提出使用层级注意力机制进行语法错误改正（grammatical error correction）。在这篇文章中，在编码阶段使用GRU进行编码，但是为了解决OOV (out-of-vocabulary)问题，作者提出了所谓的Hybrid encoder，即对于不在词表中的词（UNK），使用字母编码向量代替UNK，这个并非本文讨论的重点，因此下面我们集中讨论这篇文章中top-down层级注意力机制：word-level attention和character-level attention。

语法错误改正的特点正好和文本分类相反，文本分类是需要从词到句再到文档一层一层抓住文本所描述的语义，而语法错误改正是需要先理解文本的语义，然后根据语义对其中的词进行修改。词的修改也并不是修改全词，有可能只是其中几个字母的错误，因此需要用top-down层级注意力机制。

目标词的确定是通过以下两种方式：

1. 如果目标词在词表内，则使用word-level attention
2. 如果目标词不在词表内，则使用character-level attention

具体来说就是：

1. 以词为基础利用GRU进行句子编码（此处的编码指的是Hybrid encoder），得到隐状态$\mathbf{h}_1, \mathbf{h}_2, …, \mathbf{h}_T$；

2. 对于源词和目标词都在词表中的情况，直接使用word-level注意力权重进行解码，生成目标序列；

3. 对于目标词不在词表的情况（模型预测出来的目标词为UNK），$p(UNK|\mathbf{x}_c)\cdot p(char_seq|\mathbf{x}_c)$；

4. 其中character-sequence的生成方法如下：

   初始化character-decoder隐状态：$\mathbf{d}_s^\sim = Relu(W[\mathbf{c}_s;\mathbf{d}_s])$，其中$\mathbf{c}_s=\sum_T\alpha_j\mathbf{h}_j$，$\mathbf{d_s}$表示当前word-decoder的隐状态；

   • 若目标词对应的源词在词表中，直接使用character-decoder生成一个词；
   • 若目标词对应的源词也不在此表中（即源词和目标词都为UNK），首先使用character-decoder生成一个词，然后利用编码时使用的character-encoder得到的UNK源词编码与生成的词进行加权求和即得到目标词
   $$\mathbf{d}_n^{cc} = Relu(W_c[\mathbf{c}_n^c;\mathbf{d}_n^c])$$

另外，这种自上而下的注意力机制还被应用于为唱片挑选合适的海报Yu et al., 2017以及文本生成，这里就不详细介绍了。总的来说想这种需要先从全局信息来确定局部信息的场景都可以使用这种从上而下的层级注意力机制。

3.3 自注意力机制

回顾一下基础的注意力机制：给定一个序列$V=\{\mathbf{v}_i\}$和模式向量$\mathbf{u}$，对于每一个$\mathbf{v}_i$我们都可以计算一个注意力权重$\alpha_i=softmax(a(\mathbf{v}_i, \mathbf{u}))$。实际上这种注意力机制是一种外部注意力，正如前面我们讨论的，这种注意力实际上有点类似于计算$\mathbf{v}_i$与外部模式向量$ \mathbf{u}$的匹配度（或者相似度），注意力权重依赖于外部模式。

所谓自注意力机制指的是$\mathbf{u}$是输入序列自身的一部分，即：

$$e_{ij} = a(\mathbf{v}_i, \mathbf{v}_j)$$ $$\alpha_{ij} = softmax(e_{ij})$$

通常情况下，

$$\alpha_{ij} = softmax(tanh(\mathbf{w}^T[\mathbf{v}_i;\mathbf{v}_j]+b))$$

那么自注意力机制通常在什么场景下使用呢？

• 获取序列内部元素之间的相互依赖关系。比如”Volleyball match is in progress between ladies“，这句话中其他词都是在围绕match进行描述的。从上面的形式描述也可以看出，自注意力机制是在计算序列内部元素之间的匹配度，因此当我们需要获取序列内部的依赖关系的时候自注意力机制就可发挥作用。

• 通过语义获取词义，类似于词义消歧。举个例子：

  I arrived at the bank after crossing the street.

  I arrived at the bank after crossing the river.

  其中bank再第一句中最可能的意思应该是银行， 而第二句中的bank最可能的语义应该是岸边。因为自注意力能使第一句中的bank注意到street，而第二句中的bank注意到river。

自注意力机制最成功的的案例应该属于最近大火的Transformer了，下面我们会对Transformer进行单独的介绍，这里就先跳过。

3.4 基于记忆力的注意力机制

为了介绍基于记忆力的注意力机制，我们重新构建旧的注意力机制。

假设有一组键值对$V =\{(\mathbf{k}_i, \mathbf{v}_i)\}$和一个检索向量（query vector）$\mathbf{q}$，重新定义注意力权重计算过程：

$$e_i = a(\mathbf{k}_i, \mathbf{q})$$ $$\alpha_i = softmax(e_i)$$ $$\mathbf{c} = \sum_i \alpha_i \mathbf{v}_i$$

这种注意力机制有点类似信息检索，给定一些文本和一个检索词，根据这些文本与检索词之间的匹配度（注意力权重$\{\alpha_i\}$）提取文本中的信息。当然信息检索是根据文本与检索词之间的匹配度进行文本排序，这里不做讨论。需要注意的是，如果所有的$\mathbf{k}_i=\mathbf{v}_i$的话，基于记忆力的注意力机制又转化成基础的注意力机制。更多关于$\mathbf{k}$和$\mathbf{v}$的内容我们会在Transformer专题里面进行讨论。

下面我们从两个方面详细讨论基于记忆力的注意力机制相对于基础记忆力机制的优势：

• 可复用性（Reusability）

  对于问答系统来说，一个基本的问题是答案与问题并不是直接相关的，举个例子：

  1. Sam walks into the kitchen.
  2. Sam picks up an apple.
  3. Sam walks into bedroom.
  4. Sam drops the apple.

  Q: Where is the apple?

  上面四个句子与apple匹配度比较高的应该是第2和第4句话，在用基础注意力机制的时候，注意力权重会集中在这两句话上，但是我们知道正确答案却在第3句话。因此，基础注意力机制没有办法解决这种间接相关（或者说需要进行一定程度上的推理）的任务。

  但是如果我们通过迭代更新记忆信息来模拟时序推理的话，这个问题就可以得到解决。Sukhbaatar et al., 2015通过结合记忆神经网络和注意力机制，为这类问题提出了一种解决方案。这里我们只讨论Sukhbaatar et al., 2015的论文中的注意力机制和记忆力神经网络结合的部分，其他的细节问题不做讨论，过程如下：

  1. 初始化$\mathbf{q}_t=\phi_q(question)$；
  2. 计算句向量$\mathbf{k}_i=\phi_k(x_i )$；
  3. $e_i=\mathbf{q}_t^T\mathbf{k}_i$；
  4. $\alpha_i=softmax(e_i)$；
  5. $\mathbf{v}_i=\phi_v(x_i)$；
  6. $\mathbf{c}_i=\sum_i \alpha_i \mathbf{v}_i$；
  7. 更新问题向量$\mathbf{q}_{t+1}=\mathbf{q}_{t}+\mathbf{c}_i$；
  8. 重复$2-7$

  我们对上面的过程做一个解释：

  第一步：初始化问题，将问题转化成向量，需要注意这里是一个一维向量，不是多个词向量序列构成的句矩阵，包括下面$x_i$指的是一个句子而不是词。$\phi_q, \phi_k, \phi_v$都是将句子转化成一维的向量，具体怎么转化的在文章中有具体的介绍，这里不是我们讨论的重点。

  第二步：将第$i$个句子转化成句向量。

  第三至第六步：就是标准的注意力加权求和。

  第七步：更新问题向量。

  整个推理过程如下：

  

  另外有很多人在这方面也做了很多工作，比如Kumar et al. 2016，Graves et al., 2014这里不详细介绍了。下面我们继续介绍第二点优势。

• 灵活性（Flexibility）

  由于键 和值 有不同的向量表示，我们就可以自由的设计相应的嵌入层更好的获得相应的信息，比如分别设计针对问题和答案的向量表示，比如Miller et al., 2016提出的key-value memory network：设计一个窗口结构，窗口中心的词为值向量，而窗口周围的词为键向量，用上面的例子则apple和bedroom为值向量，他们周围的词为键向量。

  如果我们希望使用基础的注意力机制只需要令$\mathbf{k}=\mathbf{v}$即可，这也是其灵活性的表现。另外还有一些其他的键值向量的设计方式，这里我们不再过多介绍了。

3.5 指针网络

对于一些排序的问题（sorting）或者“巡回推销员”（travelling salesman）问题输出并不是确定的，而是随着输入的变化输出也随之改变。面对这类问题前面提到的各种注意力模型都无能为力了，因此 Vinyals, et al. 2015提出了指针网络的方法。不同于其他注意力模型将上下文信息糅合进一个向量里面，指针网络是在解码阶段通过注意力机制一个一个从输入序列中选择元素进行输出。

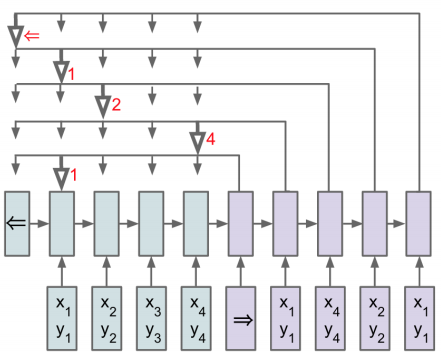
给定一个输入序列$V=\{\mathbf{v}_i\}$，指针网络输出一个序列$\mathbf{c}=\{c_i\}$，其中$c_i$是$V$中元素的索引。

$$\begin{align} y_i &= p(c_i|c_1,...c_{i-1}, V) \nonumber\\ &= \sigma(a(\mathbf{v}_i, \mathbf{u})) \nonumber\\ &= \sigma(\mathbf{w}_2^{T}tanh(W_1[\mathbf{v}_i;\mathbf{u}])) \nonumber \end{align}$$

3.6 特定任务下的注意力机制

• 文本摘要

Tan et al., 2017在文本摘要任务中提出了一种类似于PageRank的graph-based attention。给定一篇文档$V=\{\mathbf{v}_i\}$，其中$\mathbf{v}_i$表示句子向量， 假设注意力分布为$\mathbf{\alpha}=\{\alpha_i\}$，则$\mathbf{\alpha}$满足一下条件：

$$\mathbf{\alpha}(t+1)=\lambda WD^{-1}\mathbf{\alpha}(t)+(1-\lambda)\mathbf{y}$$

其中$W$表示方阵$W(i,j)=\mathbf{v}_i^TM\mathbf{v}_j$，其中M是一个待学习的权重矩阵。$D$是一个对角矩阵，对角线上的元素$d_i=W(i,i)$，这是为了保证$WD^{-1}=1$，$\lambda$是一个阻尼系数，$\mathbf{y} \in \mathbb{R}^n$，并且$\mathbf{y} $中的所有元素都是$1/n$。

我们来考虑下这个注意力的物理意义是什么？忽略阻尼系数$\lambda$，我们来看下$WD^{-1}$表示什么：

$$WD^{-1} =(\mathbf{v}_i^TM\mathbf{v}_j)D^{-1}$$

其中的$W$与之前的$e_i$何其相似（公式$(9) $），而$D^{-1}$的存在是为了保证这一项能各元素相加为$1$，这又与$softmax(e_i)$何其相似。也就是说$WD^{-1}$我们也可以看成是一个注意力权重，而这个注意力权重是把注意力放在另一个注意力上。从公式$(32)$我们可以看出$\alpha_i(t)$注意力越大$\alpha_i(t+1)$也就会越大。也就是说，如果一个句子与其他重要的句子有更多的关联性的话，那么这个句子也会更重要。这个思想如同我们前面提到的和PageRank非常相似。

• 机器翻译

Luong et al., 2015为了解决机器翻译过程中，对长序列的所有元素都计算注意力太过消耗资源，因此提出一个叫做局部注意力机制（local attention）的方法。

所谓局部注意力机制其实很简单，就是从整个序列中设定一个窗口$D$，选取$[p_t-D, p_t+D]$范围内的序列计算注意力。其中$p_t$有两种确定方法：

1. 假设源序列和目标序列是一一对应的，则$p_t=t$，即以步长为1沿着序列依次向后滑动窗口取子序列；
2. 假设源序列和目标序列并不是一一对应的，则$p_t=S\cdot sigmoid(\mathbf{v}_p^Ttanh(W_p\mathbf{h}_t))$，其中$S$表示序列的源总长度。然后计算注意力权重，最后视同高斯平滑得到输出。

• 其他

除了以上介绍的各种各样的注意力机制以外，Kim et al., 2017还提出一种叫做结构化注意力机制的方法。这种注意力机制可用于处理序列选择性问题，例如从一个序列中选出一个子序列，或者从语法树中选取一个子树。基本方法是将注意力模型看成是条件随机场（CRF），引入一个隐变量$Z={\mathbf{z}_i}$，然后对序列进行编码-解码。这里不再详细介绍这种方法了，如有兴趣可以看论文原文。

4. 小结

从上面的介绍我们可以看到，注意力机制的强大之处几乎在NLP领域的各个任务中都有相当出色的发挥：

• 机器翻译，作为最先引入注意力机制的任务，注意力机制使得机器翻译的水平比之前有一个大的飞跃；
• 多模式理解，使用多维注意力机制使我们能从不同角度理解自然语言
• 文本分类，使用自下而上的层级注意力机制提升文本分类的能力
• 语法纠正，自上而下的注意力机制帮助我们完成这类人物
• 语言模型，自注意力机制，尤其是Transformer的横空出世，使得语言模型的水准达到了前所未有的高度
• 阅读理解，基于记忆力的注意力机制使得注意力机制具有了推理能力，帮助我们完成阅读理解的任务
• 文本摘要，在基于图的注意力机制下，完成了类似PageRank的抽取式文本摘要，虽然目前没有看到其在信息检索方面的研究，但是我相信把它应用于信息检索领域也会有不俗的表现
• 序列排序，指针网络的出现补足了注意力机制在排序方面的应用空白
• 另外对于分词，分块，语法解析等基础任务同样有相关的注意力机制的研究成果

从上面的总结我们不难得出一个结论：Attention is all you need 此言非虚！

5. 参考资料

1. An Introductory Survey on Attention Mechanisms in NLP Problems, Dichao Hu, 2018
2. Neural Machine Translation by Jointly Learning to Align and Translate, Bahdanau et al., 2014
3. Effective Approaches to Attention-based Neural Machine Translation, Luong et al., 2015
4. Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention), Jay Alammar
5. Neural Turing Machines, Graves et al., 2014
6. NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE, Bahdanau et al., 2015
7. Attention is all you need, Vaswani et al., 2017
8. Coupled multi-layer attentions for co-extraction of aspect and opinion terms, Wang et al., 2017
9. A STRUCTURED SELF-ATTENTIVE SENTENCE EMBEDDING, Lin et al., 2017
10. Hierarchical attention networks for document classification, Yang et al., 2016
11. A nested attention neural hybrid model for grammatical error correction, Ji et al., 2017
12. Hierarchicallyattentive rnn for album summarization and storytelling, Yu et al., 2017
13. End-toend memory networks, Sukhbaatar et al., 2015
14. Ask me anything: Dynamic memory networks for natural language processing, Kumar et al., 2016
15. Key-value memory networks for directly reading documents, Miller et al., 2016
16. Pointer Networks, Vinyals, et al., 2015
17. Abstractive document summarization with a graph-based attentional neural model, Tan et al., 2017
18. Structured attention networks, Kim et al., 2017